
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графики (номограммы) для решения задач нестационарной теплопроводности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где
Решения (9.10) представлены в виде простых и удобных номограмм, которые могут быть двух видов. Номограммы построены для двух случаев:
Зависимость (9.10) справедлива также для цилиндра и шара.
Для решения прямой задачи определения температуры в центре либо на поверхности пластины через какой-то момент времени после её охлаждения в среде с
В любом сечении температура находится с помощью решения (9.9). Теплоотдача при турбулентном течении жидкости в трубах Турбулентный режим-при Re>10000 Коэффициент теплоотдачи рассчитывается по формуле Михеева:
0.7<Pr<200 4*103<Ref<106 где
Петуховым получена формула из гидродинамической аналогии Рейнольдса для расчета коэффициента теплоотдачи капельной жидкости(не газов):
n= 0,11(нагрев) n=0,25(охлажд) Переходный режим. Переходный режим существует при
Формула Михеева с точностью ±15% описывает теплообмен очень многих жидкостей. По этой формуле (14.7) рассчитывается теплообмен при движении жидкости внутри труб кожухотрубных теплообменников. 58)Частные случаи охлаждения (нагрева) неограниченной пластины Анализ решения дифференциального уравнения одномерной теплопроводности записанного для неограниченной пластины (9.9) в виде бесконечного, быстросходящегося ряда предполагает три характерных случая: 2)
Так как распределение температуры в теле определяется как внутренним термическим сопротивлением, так и внешним, то для инженерных расчётов при
2)
3)
Каждому значению числа Bi отвечает своя совокупность корней уравнения (9.9). Расход теплоты каждым м3 охлаждаемой пластины за время от
где С – теплоёмкость материала пластины; r – плотность пластины; J0 – начальная избыточная температура; `J – средняя избыточная температура по толщине пластины в момент t1.
59)Гидродинамические числа подобия Найдём условия подобия двух потоков несжимаемой жидкости, которые описываются уравнением движения Навье-Стокса. Рассмотрим только уравнение движения для проекции скорости на ось Х:
Аналогично запишем для второй подобной системы (13.2) (всё с двумя штрихами). Вводим постоянные подобия (константы):
Выражаем уравнение движения Навье-Стокса для второй подобной системы через первую с учётом постоянных подобия
Из (13.3) выделим пять комплексов подобия:
 . .
Для получения числа подобия разделим второй комплекс на первый: Комплексы, составлены из констант подобия, когда справа или слева стоит 1, получили название индикатора подобия, заменяя в индикаторе подобия безразмерные константы подобия где Но выражает меру переносного или конвективного ускорения к ускорению в данной точке. Разделив II на III получаем число подобия Фруда:
где Fr характеризует отношение инерционной силы в потоке к силе тяжести. Разделив IV на II, мы получаем число подобия Эйлера:
где Eu отношение перепада давления в потоке жидкости к динамическому давлению потока. Разделив II на V, получаем основное число гидромеханического подобия Рейнольдса Re:
где Re характеризует режим движения потока, и представляет собой меру отношения сил инерции к силам вязкости.
Архимед, Галилей и Грасгоф являются производными числами подобия.
60 нужны особенности течения жид-ти, но --- Теплоотдача в ламинарном пограничном слое при продольном омывании пластины. Теория гидродинамического пограничного слоя дана Прандтлем в 1904 году. Сущность теории пограничного слоя состоит в упрощении дифференциального уравнения конвективного теплообмена применительно к пограничному слою. Прандтлем была решена задача при продольном обтекании плоской пластины движущимся потоком жидкости при длине пластины l и ширине, равной единице. Теория Прандтля справедлива только для неразряженных газов и для кипящих жидкостей (
1 – пограничный слой (динамический – (а) и тепловой – (б)); 2 – невозмущённый поток жидкости; I – зона ламинарного режима течения; II – зона переходного режима течения; III – зона турбулентного режима течения; IV – зона вязкого ламинарного подслоя. При соприкосновении частиц жидкости с поверхностью тела они «прилипают» к ней. В результате в области около пластины вследствие действия сил вязкости возникает тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущённого потока. Ламинарным называется такое движение, при котором возможно существование стационарных траекторий частиц жидкости. Турбулентным называется движение жидкости с хаотично изменяющимися во времени траекториями частиц жидкости, при котором в потоке возникают нерегулярные пульсации скорости, давления, плотности, неравномерно распределённых в потоке. Толщина гидродинамического пограничного слоя Принимаем, что поперёк динамического пограничного слоя давление не изменяется, т.е. Для плоского безградиентного стационарного течения вязкой жидкости в пограничном слое у плоской поверхности уравнение движения Навье-Стокса (11.12) упрощается до вида (в проекции на ось ОХ):
Уравнение сплошности имеет вид:
Из четырёх неизвестных ( Аналогично понятию гидродинамического пограничного слоя Кружилиным Г.Н. было введено понятие теплового пограничного слоя. Толщина теплового пограничного слоя определяется как расстояние по нормали к поверхности, на котором температура изменяется от Изменение температуры происходит в очень маленькой пространственной области ( Для стационарного течения уравнение энергии (11.18) упрощается до: Полученная система дифференциальных уравнений (12.1), (12.2) и (12.3) описывает конвективный теплообмен только в ламинарном пограничном слое.
Прандтль впервые выполнил приближённое решение этой системы дифференциальных уравнений, а точнее уравнение движения (12.1) методом интегральных соотношений Кáрмана для ламинарного пограничного слоя при продольном обтекании плоской пластины и получил, что толщина динамического пограничного слоя определяется из выражения
где Rex – локальное значение числа Рейнольдса, которое характеризует соотношение сил инерции х – расстояние от передней коронки пластины, м.
В пограничном слое силы вязкости и инерционные силы соизмеримы, в невозмущённом потоке преобладают силы инерции. Введя понятие локального коэффициента трения в следующей форме где tw(x) – касательное напряжение на пластине на расстоянии х от передней кромки, Прандтлем было получено приближенное решение для Сt:
Приближённое решение дифференциального уравнения энергии (12.3) при числе Прандтля где При Учитывая (12.4) мы получаем толщину
Значение числа Pr берётся из справочной таблицы. Для газов Связь между локальным коэффициентом теплопередачи aх на расстоянии х (м) от передней кромки пластины и локальным коэффициентом трения определяется на основе аналогии Рейнольдса, переноса теплоты и количества движения. При (St – число Стантона – аналогия переноса теплоты и количества движения при Pr = 1)
Коэффициент теплоотдачи a обратно пропорционален толщине пограничного слоя (с ростом расстояния х dт увеличивается, а a уменьшается). Формула (12.13) хорошо описывает теплопередачу газов при небольших температурных напорах.
Для приведения выражения (12.14) к безразмерному виду, умножим его части на Найдя число Нуссельта можно определить локальный коэффициент теплоотдачи:
Для газов Формула (12.15) справедлива при
Средний коэффициент теплоотдачи при ламинарном течении при продольном обтекании плоской пластины определяется из следующего уравнения (учитывая St = Ct / 2)
(12.16)
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.85.96 (0.009 с.) |

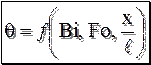 , (9.10)
, (9.10) – безразмерная координата;
– безразмерная координата;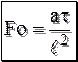 – число подобия Фурье (безразмерное время).
– число подобия Фурье (безразмерное время). – центр пластины
– центр пластины – поверхность пластины
– поверхность пластины
 , при заданных размерах
, при заданных размерах  , материале пластины l, и a находится
, материале пластины l, и a находится  . Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна:
. Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна: .
. ,(14.7)
,(14.7) – поправка на начальн участок гидродинамич-ой стабилизации. При x/d < 15 она может быть найдена по формуле
– поправка на начальн участок гидродинамич-ой стабилизации. При x/d < 15 она может быть найдена по формуле .Если x/d > 15
.Если x/d > 15  ,
, . Он является неустойчивым, поэтому плохо изучен, для него нет критериальных зависимостей. Для расчёта этого режима используется формула Михеева (14.7) с введением поправки.
. Он является неустойчивым, поэтому плохо изучен, для него нет критериальных зависимостей. Для расчёта этого режима используется формула Михеева (14.7) с введением поправки. (
( ). В этом случае с достаточной точностью можно ограничится первым членом ряда, и распределение температуры в неограниченной пластине будет иметь вид:
). В этом случае с достаточной точностью можно ограничится первым членом ряда, и распределение температуры в неограниченной пластине будет иметь вид:
 в уравнении (9.9) можно ограничится первым членом ряда, так как термическое сопротивление
в уравнении (9.9) можно ограничится первым членом ряда, так как термическое сопротивление  , то температура на поверхности пластины становится равной температуре окружающей среды, т.е.
, то температура на поверхности пластины становится равной температуре окружающей среды, т.е.  .
. (
( ). Процесс выравнивания температуры в теле происходит значительно быстрее, чем отвод теплоты с поверхности пластины. Распределение температуры в этом случае показано на рисунке (9.7).
). Процесс выравнивания температуры в теле происходит значительно быстрее, чем отвод теплоты с поверхности пластины. Распределение температуры в этом случае показано на рисунке (9.7).
 (Реальный случай).
(Реальный случай).
 до
до  определяется по формуле:
определяется по формуле: ,
, (13.1)
(13.1) ;
;  ;
;  ;
;  ;
; ;
;  ;
;  .
. (13.3)
(13.3) .
. .
.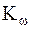 ,
,  ,
,  на размерные величины w, t,
на размерные величины w, t,  , (13.4)
, (13.4) , (13.5)
, (13.5) , (13.6)
, (13.6) , (13.7)
, (13.7)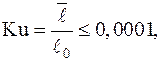 где
где  – длина свободного пробега молекулы,
– длина свободного пробега молекулы, 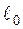 – характерный размер (длина пластины)).
– характерный размер (длина пластины)).
 определяется как расстояние по нормали от пластины, на которой продольная составляющая скорости достигает своего максимального значения, равного скорости невозмущённого потока
определяется как расстояние по нормали от пластины, на которой продольная составляющая скорости достигает своего максимального значения, равного скорости невозмущённого потока  . Ввиду малой толщины пограничного слоя (
. Ввиду малой толщины пограничного слоя ( ) удаётся упростить дифференциальное уравнение движения Навье-Стокса.
) удаётся упростить дифференциальное уравнение движения Навье-Стокса. . Во внешнем потоке (2) из уравнения Бернулли следует, что давление также не изменяется:
. Во внешнем потоке (2) из уравнения Бернулли следует, что давление также не изменяется:  .
. , (12.1)
, (12.1) .
. . (12.2)
. (12.2) ) остались две переменные
) остались две переменные  и
и  , что значительно упрощает решение дифференциальных уравнений (12.1) и (12.2).
, что значительно упрощает решение дифференциальных уравнений (12.1) и (12.2). до
до  . Внутри теплового пограничного слоя
. Внутри теплового пограничного слоя  , а на внешней его границе
, а на внешней его границе  .
. ), следовательно, можно пренебречь теплопроводностью вдоль слоя по сравнению с теплопроводностью поперёк слоя, т.е.
), следовательно, можно пренебречь теплопроводностью вдоль слоя по сравнению с теплопроводностью поперёк слоя, т.е.  , т.к.
, т.к.  .
. . (12.3)
. (12.3) , (12.4)
, (12.4) ,
, и сил вязкости (n) в сечении х;
и сил вязкости (n) в сечении х;
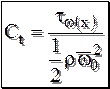 , (12.6)
, (12.6) . (12.7)
. (12.7) (для газов
(для газов  , для жидких металлов
, для жидких металлов 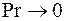 , для капельных жидкостей
, для капельных жидкостей  , для масел
, для масел  ), было получено, что отношение толщины теплового пограничного слоя к толщине динамического пограничного слоя при его ламинарном движении:
), было получено, что отношение толщины теплового пограничного слоя к толщине динамического пограничного слоя при его ламинарном движении:  . (12.10)
. (12.10) – физический параметр.
– физический параметр. толщина теплового слоя равна толщине динамического пограничного слоя. При
толщина теплового слоя равна толщине динамического пограничного слоя. При 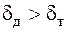 происходит нагревание жидкости от пластины. При
происходит нагревание жидкости от пластины. При  происходит охлаждение жидкости от пластины.
происходит охлаждение жидкости от пластины. . (12.11)
. (12.11) .
. , (12.12)
, (12.12) – аналогия Рейнольдса. (12.13)
– аналогия Рейнольдса. (12.13)
 . Получим критериальное уравнение для расчёта местного (локального) коэффициента теплоотдачи, при продольном обтекании пластины ламинарным потоком жидкости (с учётом (12.11)).
. Получим критериальное уравнение для расчёта местного (локального) коэффициента теплоотдачи, при продольном обтекании пластины ламинарным потоком жидкости (с учётом (12.11)). .
.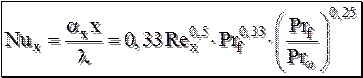 . (12.15)
. (12.15) .
.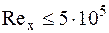 ,
,  . Prf берётся из таблиц при температуре жидкости, Prw берётся из таблиц при температуре стенки.
. Prf берётся из таблиц при температуре жидкости, Prw берётся из таблиц при температуре стенки. .
. ,
,


