
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематический коэффициент вязкостиСодержание книги
Поиск на нашем сайте
Для капельных жидкостей – с увеличением температуры вязкость уменьшается, а для газов – с увеличением температуры вязкость возрастает. Коэффициент объёмного расширени Он показывает изменение объёма (плотности) при изменении температуры на 1 градус в изобарном процессе. Для газов: Для капельных жидкостей: где rж – плотность жидкости при температуре среды Тж, кг/м3; rпов – плотность жидкости при температуре стенки Тпов, кг/м3. Способность газа изменять свою плотность при изменении давления называется сжимаемостью газа. Коэффициент изотермического сжатия Мерой сжимаемости газа является число Маха: где w – скорость движения газа, м/с; а – скорость движения звука в данном газе, м/с. Когда газ движется с небольшой скоростью Для воды для воздуха Таким образом, сжимаемость воздуха в 20000 раз больше чем сжимаемость воды. Из уравнения (11.1) следует, что плотность теплового потока в любой точке жидкости однозначно определяется, если известны поля температур Ñt, удельные энтальпии h, поле скорости
Для идеального газа Теплопередача – процесс теплообмена между двумя средами (теплоносителями), разделёнными стенкой (перегородкой). В этом случае при граничных условиях III-рода задаются температуры сред теплоносителей, коэффициенты теплоотдачи
Требуется найти плотность теплового потока, тепловой поток и температуру поверхности стенки. Согласно закону Ньютона-Рихмана плотность теплового потока между горячей средой и поверхностью стенки:
По закону Фурье этот же поток передаётся теплопроводностью:
Этот же тепловой поток согласно закону Ньютона-Рихмана от наружной поверхности стенки отдаётся холодной среде:
Выражая из этих уравнений разности температур и складывая между собой, мы окончательно получаем выражение для плотности теплового потока q:
Обозначим величину
К – коэффициент теплопередачи через плоскую однослойную однородную стенку. Он представляет собой количество теплоты, передаваемое в единицу времени через единицу поверхности при разности температур между средами в один градус. Значения коэффициентов теплопередачи для различных видов теплообмена будут даны в таблице в разделе конвективного теплообмена. Коэффициент теплопередачи всегда меньше меньшего α. Для того чтобы увеличить теплопередачу, нужно увеличить меньшее α.
Тепловой поток
Величина обратная коэффициенту теплопередачи – полное термическое сопротивление теплопередачи:
где
Полное количество теплоты, передаваемое через стенку за время τ
Коэффициента теплопередачи не является термофизическим коэффициентом, его нет в справочниках. Он рассчитывается по формуле (3.11). Из (3.9) легко найти температуры горячей и холодной стенок:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.96 (0.007 с.) |

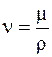 ,
, 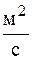 .
.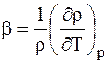 ,
, 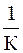 .
.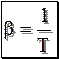 ,
, 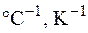 .
. .
. , Па-1.
, Па-1. ,
,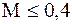 , то сжимаемостью газа пренебрегаем. В дальнейшем газы рассматриваем как несжимаемые.
, то сжимаемостью газа пренебрегаем. В дальнейшем газы рассматриваем как несжимаемые.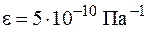 ;
; .
. . Чтобы найти эти поля (Ñt, h,
. Чтобы найти эти поля (Ñt, h,  .
. , т.е., зная поле температур, можно определить поле энтальпий. Этими дифференциальными уравнениями, описывающими поле температур и скоростей, являются уравнение сплошности (неразрывности), уравнение движения и уравнение энергии. 85Теплопередача через плоскую однослойную стенку при граничных условиях III-рода
, т.е., зная поле температур, можно определить поле энтальпий. Этими дифференциальными уравнениями, описывающими поле температур и скоростей, являются уравнение сплошности (неразрывности), уравнение движения и уравнение энергии. 85Теплопередача через плоскую однослойную стенку при граничных условиях III-рода между горячей средой и стенкой и
между горячей средой и стенкой и  между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности
между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности  и толщина стенки δ.
и толщина стенки δ.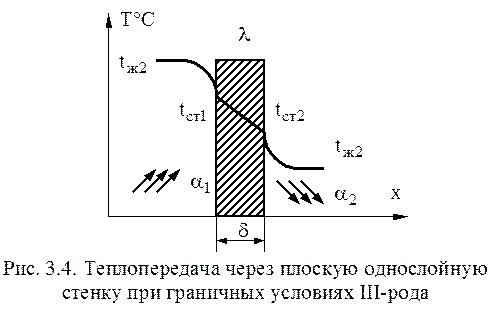
 . (3.9)
. (3.9)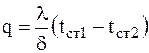 . (3.9)
. (3.9)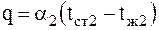 . (3.9)
. (3.9) ,
, 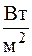 . (3.10)
. (3.10)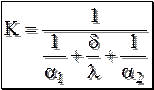 ,
,  (3.11)
(3.11) . (3.12)
. (3.12) . (3.13)
. (3.13)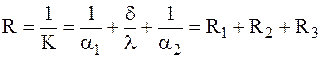 , (3.14)
, (3.14)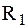 – термическое сопротивление теплоотдачи со стороны горячей жидкости;
– термическое сопротивление теплоотдачи со стороны горячей жидкости; – термическое сопротивление стенки (чем меньше l, тем выше
– термическое сопротивление стенки (чем меньше l, тем выше 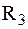 – термическое сопротивление теплоотдачи от стенки к холодной среде.
– термическое сопротивление теплоотдачи от стенки к холодной среде.  .
. , Дж.
, Дж. , (3.15)
, (3.15)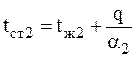 .
.


