
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоотдача при поперечном обтекании одиночной круглой трубы.Содержание книги
Поиск на нашем сайте
При поперечном омывании трубы при значении числа Рейнольдса При дальнейшем увеличении числа Рейнольдса угол отрыва вырастает с 80° до 440°. В лобовой точке набегания потока поток разделяется на две части, на поверхности трубы образуется пограничный слой, который имеет начальную толщину в лобовой точке, и далее постепенно нарастает в размерах. Скорость слоёв жидкости, примыкающих к внешней границе пограничного слоя, увеличивается вдоль периметра трубы, а давление в соответствии с уравнением Бернулли
При достижении угла атаки Имеем следующий график распределения коэффициента теплоотдачи по периметру трубы в зависимости от угла атаки j:
Кормовая часть трубы омывается и поэтому коэффициент теплоотдачи возрастает. На кривой 2 … Второй минимум соответствует месту отрыва турбулентного пограничного слоя – примерно 140°. За местом отрыва труба омывается вихрями (отрезок се), теплоотдача возрастает. Определяющий размер – внутренний диаметр dвн, определяющая температура – средняя температура жидкости. Точка b на графике 2 соответствует отрыву ламинарного пограничного слоя и образованию вихрей. Т.е. точка b соответствует переходу ламинарного течения в пограничном слое в турбулентное. Точка с соответствует … пограничного слоя. Точка d – отрыв турбулентного пограничного слоя от поверхности трубы.
Различают три режима: 1) Ламинарное течение в пограничном слое:
2) Переходный режим (лобовая часть трубы омывается ламинарным пограничным слоем, а кормовая – турбулентным пограничным слоем):
3)Развитый турбулентный режим течения жидкости в пограничном слое:
При значении числа Рейнольдса Угол атаки потока – это угол между направлением потока и осью трубы. Если угол атаки j отличается от 90°, то необходимо ввести поправку в уравнение (15.2) на угол атаки:
В случае продольного омывания трубы коэффициент теплоотдачи меньше, чем при поперечном омывании. Турбулентность потока, согласно рис. 12.2, характеризуется степенью турбулентности:
 . .
25) Теплопередача через плоскую стенку (при граничных условиях III рода) Теплопередача – процесс теплообмена между двумя средами (теплоносителями), разделёнными стенкой (перегородкой). В этом случае при граничных условиях III-рода задаются температуры сред теплоносителей, коэффициенты теплоотдачи
Требуется найти плотность теплового потока, тепловой поток и температуру поверхности стенки. Согласно закону Ньютона-Рихмана плотность теплового потока между горячей средой и поверхностью стенки:
По закону Фурье этот же поток передаётся теплопроводностью:
Этот же тепловой поток согласно закону Ньютона-Рихмана от наружной поверхности стенки отдаётся холодной среде:
Выражая из этих уравнений разности температур и складывая между собой, мы окончательно получаем выражение для плотности теплового потока q:
Обозначим величину
К – коэффициент теплопередачи через плоскую однослойную однородную стенку. Он представляет собой количество теплоты, передаваемое в единицу времени через единицу поверхности при разности температур между средами в один градус. Значения коэффициентов теплопередачи для различных видов теплообмена будут даны в таблице в разделе конвективного теплообмена. Коэффициент теплопередачи всегда меньше меньшего α. Для того чтобы увеличить теплопередачу, нужно увеличить меньшее α.
Тепловой поток
Величина обратная коэффициенту теплопередачи – полное термическое сопротивление теплопередачи:
где
Полное количество теплоты, передаваемое через стенку за время τ
Коэффициента теплопередачи не является термофизическим коэффициентом, его нет в справочниках. Он рассчитывается по формуле (3.11). Из (3.9) легко найти температуры горячей и холодной стенок:
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.006 с.) |


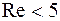 имеет место плавное безотрывное омывание внешней поверхности. С увеличением числа Рейнольдса режим становится ламинарным, а при
имеет место плавное безотрывное омывание внешней поверхности. С увеличением числа Рейнольдса режим становится ламинарным, а при  , со стороны кормовой части трубы возникают вихревые потоки и отрыв пограничного слоя. Отрыв происходит при угле атаки
, со стороны кормовой части трубы возникают вихревые потоки и отрыв пограничного слоя. Отрыв происходит при угле атаки  .
.




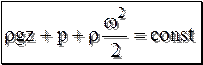 . (15.1)
. (15.1)
 скорость достигает наибольшего значения и далее начинает уменьшаться, что сопровождается соответствующим увеличением или восстановлением давления. В этой области пограничный слой становится неустойчивым.
скорость достигает наибольшего значения и далее начинает уменьшаться, что сопровождается соответствующим увеличением или восстановлением давления. В этой области пограничный слой становится неустойчивым.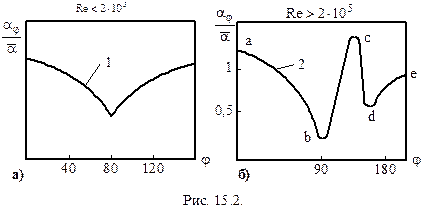
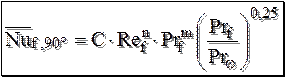 . (15.2)
. (15.2) .
.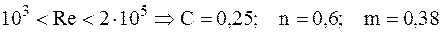 .
.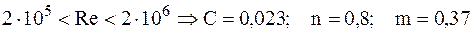 .
.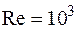 происходит изменение закона теплообмена. Уравнение (15.2) справедливо при угле атаки
происходит изменение закона теплообмена. Уравнение (15.2) справедливо при угле атаки 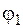 , °
, °
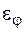



 между горячей средой и стенкой и
между горячей средой и стенкой и  между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности
между стенкой и холодной средой, т.е. задаётся закон теплообмена. Также задаётся коэффициент теплопроводности  и толщина стенки δ.
и толщина стенки δ.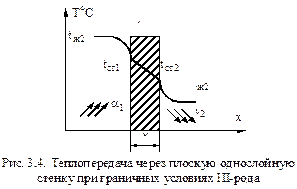
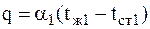 . (3.9)
. (3.9)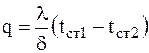 . (3.9)
. (3.9)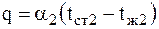 . (3.9)
. (3.9) ,
, 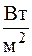 . (3.10)
. (3.10)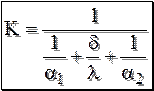 ,
,  (3.11)
(3.11) . (3.12)
. (3.12) . (3.13)
. (3.13) , (3.14)
, (3.14)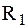 – термическое сопротивление теплоотдачи со стороны горячей жидкости;
– термическое сопротивление теплоотдачи со стороны горячей жидкости; – термическое сопротивление стенки (чем меньше l, тем выше
– термическое сопротивление стенки (чем меньше l, тем выше 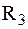 – термическое сопротивление теплоотдачи от стенки к холодной среде.
– термическое сопротивление теплоотдачи от стенки к холодной среде.  .
.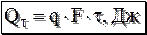 , Дж.
, Дж.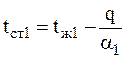 , (3.15)
, (3.15) .
.


