
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность через цилиндрическую однородную, однослойную стенку при граничных условиях I-рода.Содержание книги
Поиск на нашем сайте
Ось OZ совмещаем с осью цилиндра, и температура меняется только вдоль радиуса цилиндра.
Для полого цилиндра заданы: внешний ( Требуется найти: уравнение, описывающее температурное поле в цилиндре, т.е. изменение температуры в зависимости от диаметра d (рад. r), а также плотность теплового потока q и сам тепловой поток Q. На основании дифференциального уравнения теплопроводности при стационарном режиме и отсутствии внутренних источников теплоты (2.10), учитывая, что первая и вторая производные температуры по z равны нулю
а также то, что температура не зависит от полярного угла j, то уравнение Лапласа в цилиндрических координатах (2.10) упрощается до вида
Граничные условия дифференциального уравнения: при при Введём новую переменную
тогда дифференциальное уравнение (4.1) будет иметь вид:
Интегрируем данное выражение:
Тогда, потенциируя это выражение и переходя к первоначальным переменным мы получаем:
После интегрирования получаем:
Для определения постоянных интегрирования
Решая уравнение (а) относительно
Подставляя в (4.2) значения
Это решение описывает распределение температуры в цилиндрической стенке. Это логарифмическая кривая (рис. 4.1). Задавая произвольным диаметр, можно определить температуру в любой точке цилиндрической поверхности. Согласно закону Фурье плотность теплового потока пропорциональна градиенту температуры (температура меняется только вдоль радиуса):
Из этого выражения следует, что тепловой поток полностью определяется внутренним и наружным диаметрами цилиндра ( Тепловой поток может быть отнесён к единице длины цилиндра
Тепловой поток может быть отнесён к внутренней поверхности цилиндра
Тепловой поток, отнесённый к наружной поверхности цилиндра
Связь между различными приведёнными плотностями теплового потока следующая
Следовательно, в отличие от плоской стенки плотность теплового потока непостоянна по толщине цилиндрической стенки и определяется текущим диаметром цилиндра (чем больше текущий диаметр, тем меньше плотность теплового потока). Если коэффициент теплопроводности не является величиной постоянной, а зависит от температуры по зависимости
Подставляемые в выражение (4.9) значения Метод размерностей Полученные числа подобия и критериальные зависимости могли быть получены методом теории размерностей. Безразмерная величина – это величина с нулевой размерностью. В CИ за первичные величины приняты: – длина: L (м); – масса: m (кг); – время: T (сек); – температура: q (K); – сила тока: I (A); – сила света: J (канделла). Символическое выражение производной величины через основные называется размерностью. Любая производная единица измерения j в системе CИ может быть записана: Математическая формулировка задачи конвективного теплообмена в размерных величинах имеет следующую зависимость: Избыточная температура
имеет 9 переменных. Используем три первичных величины: При переходе к безразмерным величинам получаем:
Из (13.19) и (13.20) следует, что при переходе от размерных величин к безразмерным, число переменных сократилось с 9 до 6. Этот вывод соответствует p-теореме. p-теорема – физическое уравнение, содержащие n³2 размерных величин, из которых К³1 величин имеют независимую размерность, после приведения к безразмерному виду будет содержать (
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.249.107 (0.009 с.) |

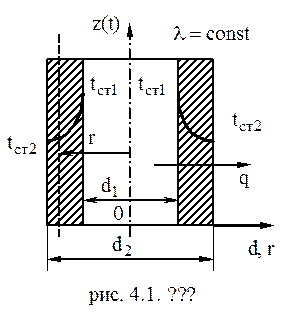
 ) и внутренний (
) и внутренний ( ) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок (
) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок ( и
и  ).
).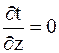 ,
,  ,
, . (4.1)
. (4.1)
 ;
;
 .
. ,
, .
. .
. .
.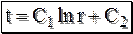 . (4.2)
. (4.2) и
и  воспользуемся граничными условиями:
воспользуемся граничными условиями: (а)
(а) , (б)
, (б) , (с)
, (с) . (4.3)
. (4.3) ;
; , Вт. (4.4)
, Вт. (4.4) и
и  ).
). ,
,  . (4.5)
. (4.5) (линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины
(линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины
 ,
, 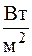 . (4.6)
. (4.6)
 ,
,  , (4.8)
, (4.8) , т.к.
, т.к.  .
.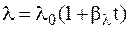 , то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения
, то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения . (4.9)
. (4.9) и
и  берутся из справочников.
берутся из справочников.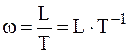 , м/с.
, м/с.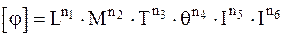 . (13.18)
. (13.18)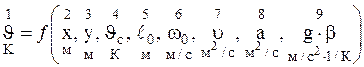 (13.19)
(13.19) , T, q, т.е.
, T, q, т.е. 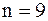 ;
; 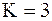 .
.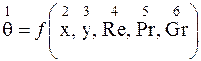 . (13.20)
. (13.20)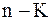 ) безразмерных величин.
) безразмерных величин.


