
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тепловой поток. Закон теплопроводности ФурьеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Температурный градиент Геометрическое место точек, имеющих одинаковую температуру, называют изотермической поверхностью. Эти поверхности не пересекаются и заканчиваются либо внутри тела, либо на его поверхности. Скорость изменения температуры вдоль определённого направления характеризует градиент температуры.
Предел отношения изменения ΔТ к расстоянию между изотермами по нормали Δn называется градиентом температуры:
где Из математики известно, т.к. объёмная производная скалярного поля является его градиентом, то для температурного поля эта производная будет градиентом температуры
где V – объём, заключённый внутри поверхности F; F – поверхность; Ñ – символический вектор (оператор Набла или Гамильтона, а также это дивергенция вектора или ротация)
Градиент температуры – вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной по данному направлению, [K/м]. Так как поле температурного градиента векторное, то символический вектор градиента
где
5. Регулярный режим нагревания (охлаждения) тел Регулярный- режим нагрев/охлажд с постоянным темпом нагрев/охлажд Темп нагрев/охлажд- относительная скорость изменения темпер в теле
Решение для тел любой формы имеет одинаковую структуру (сумма бесконечного ряда, члены которого расположены по быстро убывающим экспонентам). Например, для пластины:
коэффициент Ai не зависит ни от координат, ни от времени и находится из начальных условий
является функцией координаты (х). Экспонента убывает пропорционально времени t. Комплекс Тогда (2) примет вид:
m – постоянное число причём оно будет изменятся в зависимости от номера индекса i. Причём m1 < m2 < m3 < … < mn. При малых значениях t (рис. 9.10) распределение температуры внутри тела зависит от начального распределения температуры в теле. В этом случае температурное поле будет определяться не только первым членом (3) но и последующими. Первый период охлаждения, при котором скорость изменения температуры внутри тела зависит от вида начального распределения температуры в теле, называется неупорядоченной стадией охлаждения.
С увеличением времени последующие члены ряда (3) будут быстро убывать, т.е. ряд станет сходящимся. С момента
Логарифмируя (4) и опуская индексы получаем:
Из (5) следует, что натуральный логарифм избыточной температуры для Темп охлаждения характеризует относительную скорость изменения температуры в теле в зависимости от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела. Регулярный режим охлаждения характеризуется постоянным темпом охлаждения m во всех точках тела независимо от координаты и времени. Если экспериментально определить изменение избыточной температуры во времени и построить зависимость в полулогарифмических координатах (рис. 9.10), то из неё для случая регулярного режима можно определить:
Зависимость m от физических свойств тела, его геометрических размеров и условий теплообмена на поверхности тела можно найти из анализа теплового баланса тела. Изменение энтальпии тела равно потоку теплоты:
где r – плотность тела, V – объём тела, м3; Jv – средняя по объёму избыточная температура тела, К, °С; t – время, c. За тоже время dt вся теплота должна быть отведена с поверхности тела в окружающую среду за счёт теплоотдачи
где
Приравнивая (9.16) и (9.17) получаем:
Учитывая, что
Слева в (9.18) – темп охлаждения. Если обозначить через Темп охлаждения или относительная скорость изменения температуры в теле прямо пропорционален среднему коэффициенту теплоотдачи, поверхности тела F и обратно пропорционален теплоёмкости тела. Коэффициент пропорциональности y называется коэффициентом неравномерности распределения температуры в теле. Он зависит от условий охлаждения на поверхности тела, т.е. от числа Bi. Рассмотрим два случая: 1) Bi®0 ( В этом случае 2) Bi®¥ ( a®¥, и температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды, следовательно, При Bi®¥ (a®¥) темп охлаждения m становится прямо пропорциональным коэффициенту температуропроводности a:
Коэффициент К зависит от геометрической формы и размерности тела. Для однородной пластины: Трансцендентное уравнение для пластины было:
В (9.9) последующие корни не меньше чем предыдущие Р1 > Р2 > Р3 > …
где d – толщина пластины
Коэффициент пропорциональности для шара:
Коэффициент пропорциональности для параллелепипеда:
Коэффициент пропорциональности для цилиндра конечной длины На основной теории регулярного режима разработаны различные экспериментальные методы определения теплофизических характеристик a, l, c.
Для определения коэффициента теплопроводности l, используется l-калориметр в виде шара. Создаются условия теплообмена с конечным a; как правило, охлаждение на воздухе. При этих условиях определяется темп охлаждения. 3) При свободном движении температура жидкости в пограничном слое изменяется от Режим движения классифицируется в зависимости от числа Релея
где
Интенсивность теплоотдачи при естественной конвекции характеризуется коэффициентом теплоотдачи, который определяется из формулы Ньютона:
Таким образом, коэффициент теплоотдачи характеризует количество тепла, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и жидкостью в 1 градус. В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и поэтому различают средний по поверхности коэффициент теплоотдачи и локальный или местный соответствующий единичному элементу поверхности. По изучению интенсивности теплообмена в условиях свободного движения проведены многочисленные исследования с различными телами и различными жидкостями. В результате обобщения опытных данных получены критериальные зависимости для средних значений коэффициента теплоотдачи. В общем виде закономерность теплоотдачи может быть представлена в виде
где Значения С коэф. проп. и n зависят от режима движения среды. В принятой для исследования схеме нагрева теплообменной трубы тепловой поток является постоянным и на большей части рабочего участка (за исключением зоны, прилегающей к токопроводящим шинам) направлен от поверхности трубы в окружающую среду. Его величина определяется по электрической мощности, затрачиваемой на нагревание рабочего участка (теплообменной трубы).
Из графика вычислить величину показателя степени n, равную угловому коэффициенту прямой, построенной по экспериментальным точкам.
Первая теорема Кондратьева Если обозначить через Темп охлаждения или относительная скорость изменения температуры в теле прямо пропорционален среднему коэффициенту теплоотдачи, поверхности тела F и обратно пропорционален теплоёмкости тела. Коэффициент пропорциональности y называется коэффициентом неравномерности распределения температуры в теле. Он зависит от условий охлаждения на поверхности тела, т.е. от числа Bi. Рассмотрим два случая: 3) Bi®0 ( В этом случае 4) Bi®¥ ( a®¥, и температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды, следовательно, Вторая теорема Кондратьева При Bi®¥ (a®¥) темп охлаждения m становится прямо пропорциональным коэффициенту температуропроводности a:
Коэффициент К зависит от геометрической формы и размерности тела. Для однородной пластины: Трансцендентное уравнение для пластины было:
В (9.9) последующие корни не меньше чем предыдущие Р1 > Р2 > Р3 > …
где d – толщина пластины
Коэффициент пропорциональности для шара:
Коэффициент пропорциональности для параллелепипеда:
Коэффициент пропорциональности для цилиндра конечной длины На основной теории регулярного режима разработаны различные экспериментальные методы определения теплофизических характеристик a, l, c.
Для определения коэффициента теплопроводности l, используется l-калориметр в виде шара. Создаются условия теплообмена с конечным a; как правило, охлаждение на воздухе. При этих условиях определяется темп охлаждения. Вязкостный режим Для вязкостного режима силы вязкости являются преобладающими (отсутствует влияние естественной конвекции). Вязкостный режим более вероятен в трубах малого диаметра, когда течёт очень вязкая жидкость (например, мазут), и когда имеет место малый температурный напор между поверхностью жидкости и стенки.
Средний коэффициент теплоотдачи
где
Для вязкостного режима: Переходный режим. Переходный режим существует при
Формула Михеева с точностью ±15% описывает теплообмен очень многих жидкостей. По этой формуле (14.7) рассчитывается теплообмен при движении жидкости внутри труб кожухотрубных теплообменников. Конвективный теплообмен. Основные понятия Конвекция возможна только в текучей среде, в которой перенос теплоты связан с переносом самой среды. Конвективный теплообмен – это совместный перенос теплоты за счёт теплопроводности и конвекции. Конвекция – это перенос теплоты при перемещении жидкости или газа в пространстве с одной температурой в пространство с другой температурой. Если в единицу времени через единицу контрольной поверхности перпендикулярно к ней проходит масса жидкости,
где w – скорость жидкости, м/с; r – плотность жидкости, кг/м3, то с ней переносится плотность теплового потока конвекцией.
где h – удельная энтальпия жидкости, Конвекция теплоты сопровождается теплопроводностью, так как при движении жидкости или газа происходит соприкосновение отдельных частиц, имеющих различные температуры. Поэтому конвективный теплообмен описывается уравнением:
уравнение конвективного теплообмена. Основное уравнением конвективного теплообмена – это уравнение теплоотдачи Ньютона-Рихмана.
a – количество теплоты, воспринимаемое единицей поверхности в единицу времени при разности температур Средний коэффициент теплоотдачи:
(локальное значение коэффициента теплоотдачи) Экспериментально установлено, что коэффициент теплоотдачи a зависит от вида теплообмена и теплофизических свойств теплоносителя. В общем случае:
Все реальные жидкости и газы обладают вязкостью между слоями, движущимися с различными скоростями. Между этими слоями возникает сила внутреннего трения, которая противодействует движению (направлена в сторону, противоположную движению). Согласно закону Ньютона, эта касательная сила (S или t), отнесенная к единице поверхности, действует в плоскости, ориентированной по течению прямо пропорционально изменению скорости в направлении к нормали к этой плоскости:
где m – коэффициент пропорциональности – динамический коэффициент вязкости, Па×с; y – направление, перпендикулярное направлению движения. Условиях I-рода.) Ось OZ совмещаем с осью цилиндра, и температура меняется только вдоль радиуса цилиндра.
Для полого цилиндра заданы: внешний ( Требуется найти: уравнение, описывающее температурное поле в цилиндре, т.е. изменение температуры в зависимости от диаметра d (рад. r), а также плотность теплового потока q и сам тепловой поток Q. На основании дифференциального уравнения теплопроводности при стационарном режиме и отсутствии внутренних источников теплоты (2.10), учитывая, что первая и вторая производные температуры по z равны нулю
а также то, что температура не зависит от полярного угла j, то уравнение Лапласа в цилиндрических координатах (2.10) упрощается до вида
Граничные условия дифференциального уравнения: при при Введём новую переменную
тогда дифференциальное уравнение (4.1) будет иметь вид:
Интегрируем данное выражение:
Тогда, потенциируя это выражение и переходя к первоначальным переменным мы получаем:
После интегрирования получаем:
Для определения постоянных интегрирования
Решая уравнение (а) относительно
Подставляя в (4.2) значения
Это решение описывает распределение температуры в цилиндрической стенке. Это логарифмическая кривая (рис. 4.1). Задавая произвольным диаметр, можно определить температуру в любой точке цилиндрической поверхности. Согласно закону Фурье плотность теплового потока пропорциональна градиенту температуры (температура меняется только вдоль радиуса):
Из этого выражения следует, что тепловой поток полностью определяется внутренним и наружным диаметрами цилиндра ( Тепловой поток может быть отнесён к единице длины цилиндра
Тепловой поток может быть отнесён к внутренней поверхности цилиндра
Тепловой поток, отнесённый к наружной поверхности цилиндра
Связь между различными приведёнными плотностями теплового потока следующая
Следовательно, в отличие от плоской стенки плотность теплового потока непостоянна по толщине цилиндрической стенки и определяется текущим диаметром цилиндра (чем больше текущий диаметр, тем меньше плотность теплового потока). Если коэффициент теплопроводности не является величиной постоянной, а зависит от температуры по зависимости
Подставляемые в выражение (4.9) значения 29) Уравнение движения (уравнение Навье-Стокса)
Для вывода уравнения движения используют закон сохранения количества движения. Закон сохранения количества движения – изменение количества движения в элементе объёма жидкости (dx, dy, dz) равно результирующей всех внешних сил, приложенных к поверхности и объёму элемента.
Полная или субстанционная производная оценивает действительное ускорение, которое испытывает частица материи или субстанции проходя вдоль линии тока в поле скорости (рис. 11.1). Полная субстанционная производная для составляющей скорости вдоль оси ОХ будет равна
Аналогично для
(11.11) получаем уравнение движения для несжимаемой жидкости или уравнение Навье-Стокса:
где В векторной форме окончательное уравнение движения (или уравнение Навье-Стокса) для движущейся жидкости в гравитационном поле имеет вид:
Уравнение Навье-Стокса подтверждает второй закон Ньютона: произведение массы на ускорение равно сумме сил. Т.е. уравнение баланса количества движения соответствует второму закону Ньютона. Для частного случая, когда силами вязкого трения можно пренебречь для идеальной жидкости, уравнение Навье-Стокса превращается в уравнение Эйлера
Из (11.14) для установившегося безвихревого движения в поле силы тяжести энергетический баланс для элементарной струи жидкости описывается уравнением Бернулли:
Уравнение Навье-Стокса (11.12) определяет характер распределения скоростей в однородном потоке с постоянной скоростью. Если заданы краевые условия, начальные и граничные, то 4 уравнения сплошности (11.8) и уравнение движения (11.12) дают распределение в пространстве и во времени 4-х величин: wx, wy, wz, р. Эти распределения являются решением конкретной задачи. Чтобы найти поле распределения температур или энтальпий рассмотрим уравнение энергии Тепловое подобие Тепловое подобие – это подобие температурных полей и тепловых потоков. Рассмотрим две подобные системы (', "). Запишем уравнение энергии для одномерной задачи (температура меняется вдоль координаты Х), и уравнение теплообмена:
Введём постоянные подобия (константы). Константы подобия коэффициентов температуропроводности:
Заменяя переменные второй системы через переменные первой, мы получаем дифференциальное уравнение энергии и теплообмена для второй системы, записанное через переменные первой:
Уравнение теплообмена:
Выделим пять констант подобия:
 , ,
Разделим: Подставляя вместо постоянных подобия их размерные величины и произведя разделение переменных, мы получаем числа теплового подобия Т.е. получили число подобия Фурье Это безразмерное время, которое характеризует временное развитие процесса теплопроводности (относительная форма текущего времени).
Pe выражает соотношение между переносом теплоты за счёт конвекции и за счёт молекулярной теплопроводности. Разделив Pe/Re получаем число Прандтля Pr:
Pr характеризует физические свойства среды, он табулирован в зависимости от температуры. Разделим
Nu характеризует интенсивность теплообмена на границе раздела тепловых сред и связывает интенсивность теплоотдачи a, и температурное поле l в пограничном слое потока. (13.8 – 13.11) – основные числа числового подобия. Дадим вспомогательные числа гидродинамического и теплового подобия. Комбинируя Re и Fr можно получить число подобия Галилея:
Комбинируя Ga с параметрическим числом, характеризующим неоднородное поле плотностей
Комбинируя Nu и Pe, получаем число подобия Стантона
St есть отношение конвективного теплового потока к тому тепловому потоку, который может быть перенесён потоком жидкости. При свободной конвекции Gr характеризует подъёмную силу, возникающую в жидкости вследствие разности плотностей (учёт свободной конвекции). Число подобия Маха – отношение скорости потока к местной скорости звука. где
М характеризует сжимаемость жидкости, если St пользуется при рассмотрении развитого турбулентного течения; Pr характеризует подобие полей скоростей и температуры в движущейся среде. Число подобия Релея: Ra представляет собой критерий тепловой неустойчивости или нестабильности при свободной конвекции. Число гомохромности или Струхаля: При изучении процессов гидродинамики и теплообмена могут встретиться следующие числа подобия. Число подобие Кирпичёва: (мера отношения потока тепла подводимой к поверхности тела, к потоку отводится с поверхности внутрь тела за счёт теплопроводности). Число подобия Кондратьева: (характеризует отставание изменения температуры какой-либо точки тела от изменения температуры окружающей среды, m – темп охлаждения). Число подобия Вебера: (критерий поверхности натяжения). We характеризует процесс дробления вязких жидкостей при распыле их воздухом или паром в горелочных устройствах. (отношение сил поверхностного натяжения к силам тяжести). где s – коэффициент поверхностного натяжения, Н/м; rк – плотность капли, кг/м3; r – плотность воздуха или пара, кг/м3;
Число подобия Лященко: (характеризует гидродинамическую обстановку в слое зернистого материала (кипящего слоя) при течении жидкости или газа сквозь слой твёрдого зернистого материала). Число подобия Стокса: характеризует процесс обтекания тел запылённым потоком газа. Является мерой отношения сил инерции и сил вязкости на движущуюся в потоке частицу. Всего обобщенных переменных в теории переноса порядка 140. Переходя от размерных физических величин или первичным к безразмерным комплексам или критериям, исходя из второй теоремы подобия, можно записать критериальные зависимости следующего вида:
Начальные условия. 1) Граничные условия: так как плоскость симметрии пластины проходит через 2) При 3) при В соответствии с (9.2) общее решение (9.4) будет иметь вид: Используя начальные и граничные условия для определения постоянных интегрирования Уравнение (9.7) наиболее просто решается графически. | ||||||||||||||||
|
| Поделиться: |

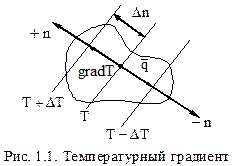
 , (1.2)
, (1.2) – единичный вектор, нормальный к изотермической поверхности, направленный в сторону возрастания температуры.
– единичный вектор, нормальный к изотермической поверхности, направленный в сторону возрастания температуры.
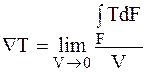 ,
, . (1.3)
. (1.3) , (1.4)
, (1.4) ,
,  ,
,  – координаты градиента;
– координаты градиента; ,
,  ,
,  – единичные векторы, имеющие направление координатных осей.
– единичные векторы, имеющие направление координатных осей. (1)
(1) (2)
(2)
 – темп охлаждения.
– темп охлаждения. (3)
(3)
 начальные условия начнут играть второстепенную роль, и процесс охлаждения полностью определяется только граничными условиями на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами, и температурное поле описывается первым членом ряда.
начальные условия начнут играть второстепенную роль, и процесс охлаждения полностью определяется только граничными условиями на границе тела и среды, физическими свойствами тела, его геометрической формой и размерами, и температурное поле описывается первым членом ряда. . (4)
. (4) , или
, или  . (5)
. (5)
 (9.16)
(9.16) ;
;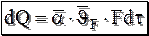 , (9.17)
, (9.17) – средний коэффициент теплоотдачи на поверхности тела.
– средний коэффициент теплоотдачи на поверхности тела. .
. .
. , и разделив левую и правую части уравнения на
, и разделив левую и правую части уравнения на  , получаем:
, получаем: . (9.18)
. (9.18) , то получим первую теорему Кондратьева:
, то получим первую теорему Кондратьева:  . (9.19)
. (9.19) ).
). и распределение температуры в теле не зависит от размеров и физических свойств тела, поэтому усреднённая температура по поверхности будет равна усреднённой температуре по объёму
и распределение температуры в теле не зависит от размеров и физических свойств тела, поэтому усреднённая температура по поверхности будет равна усреднённой температуре по объёму  , следовательно
, следовательно  .
. ).
). , коэффициент неравномерности температуры
, коэффициент неравномерности температуры  .
. , (вторая теорема Кондратьева) (9.20)
, (вторая теорема Кондратьева) (9.20)


 ; Þ
; Þ  .
.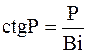 ; при Bi®¥;
; при Bi®¥;  ;
; 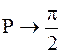 .
. Для пластины коэффициент пропорциональности K
Для пластины коэффициент пропорциональности K ,
,
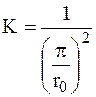 .
. .
. .
. ;
;
 – до –
– до –  , а скорость от нуля у стенки до максимума. На большом удалении от стенки скорость снова равна нулю. Скорость движения среды определяют характер (режим) движения – плёночный, ламинарный или турбулентный. С изменением характера движения изменяется и теплоотдача.
, а скорость от нуля у стенки до максимума. На большом удалении от стенки скорость снова равна нулю. Скорость движения среды определяют характер (режим) движения – плёночный, ламинарный или турбулентный. С изменением характера движения изменяется и теплоотдача. (1)
(1) – число Грасгофа;
– число Грасгофа; – число Прандтля;
– число Прандтля; (2)
(2) (3)
(3) – число Нуссельта;
– число Нуссельта; ,
, .
.

 Для пластины коэффициент пропорциональности K
Для пластины коэффициент пропорциональности K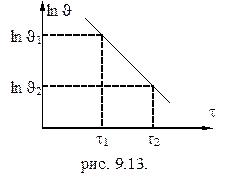
 .
. , (14.1)
, (14.1) ;
;  ,
, – отношение динамической вязкости; поправка на направление теплового потока;
– отношение динамической вязкости; поправка на направление теплового потока;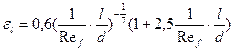
 – поправка на начальный участок тепловой стабилизации.
– поправка на начальный участок тепловой стабилизации. .
. . Он является неустойчивым, поэтому плохо изучен, для него нет критериальных зависимостей. Для расчёта этого режима используется формула Михеева (14.7) с введением поправки.
. Он является неустойчивым, поэтому плохо изучен, для него нет критериальных зависимостей. Для расчёта этого режима используется формула Михеева (14.7) с введением поправки. ,
,  ,
,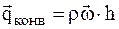 ,
, 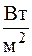 ,
, .
. (11.1)
(11.1) , (11.2)
, (11.2) ,
,  .
.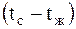 равной 1 градусу.
равной 1 градусу. .
. . (11.3)
. (11.3) , (11.4)
, (11.4)
 ) и внутренний (
) и внутренний ( ) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок (
) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок ( и
и  ).
).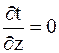 ,
,  ,
, . (4.1)
. (4.1)
 ;
;
 .
. ,
, .
. .
. .
.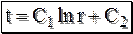 . (4.2)
. (4.2) и
и  воспользуемся граничными условиями:
воспользуемся граничными условиями: (а)
(а) , (б)
, (б) , (с)
, (с) . (4.3)
. (4.3) ;
; , Вт. (4.4)
, Вт. (4.4) и
и  ).
). ,
,  . (4.5)
. (4.5) (линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины
(линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины
 ,
, 
 ,
,  , (4.8)
, (4.8) , т.к.
, т.к.  .
.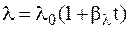 , то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения
, то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения . (4.9)
. (4.9) и
и  берутся из справочников.
берутся из справочников.
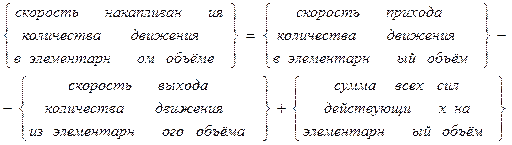
 . (11.9)
. (11.9) и
и  .
. , (11.9)
, (11.9)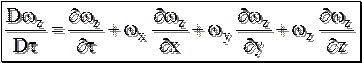 . (11.9)
. (11.9) (11.12)
(11.12) –проекции вектора ускорения свободного падения на оси.
–проекции вектора ускорения свободного падения на оси.
 ,
,  (11.13)
(11.13) . (11.14)
. (11.14)
 ,
,  (11.15)
(11.15) ,
, ,
,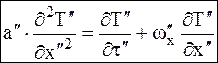 ,
, .
. ;
;  ;
;  ;
;  ;
;  ;
;  .
. .
.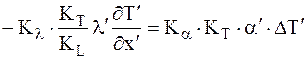 .
. .
.
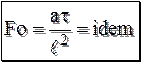 . (13.8)
. (13.8) – Число подобие Пекле
– Число подобие Пекле  , (13.9)
, (13.9)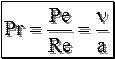 , (13.10)
, (13.10) – получим основное число теплового подобия числа Нуссельта Nu (безразмерный коэффициент теплоотдачи):
– получим основное число теплового подобия числа Нуссельта Nu (безразмерный коэффициент теплоотдачи): , (13.11)
, (13.11) . (13.12)
. (13.12) , получим число подобия Архимеда:
, получим число подобия Архимеда: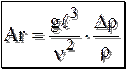 . (13.13)
. (13.13) . (13.14)
. (13.14) , где b – температурный коэффициент объёмного расширения. В результате из Ar получаем число Грасгофа Gr:
, где b – температурный коэффициент объёмного расширения. В результате из Ar получаем число Грасгофа Gr:  , (13.15)
, (13.15) , (13.16)
, (13.16) – для идеального газа,
– для идеального газа, – для реального газа.
– для реального газа. , то жидкость (газ) считаем несжимаемой;
, то жидкость (газ) считаем несжимаемой; . (13.17)
. (13.17) .
. .
. .
. .
. – размер капли (d), м.
– размер капли (d), м. .
.

 ,
, 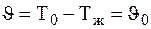 .
.  .
. , то
, то , при
, при  .
. на поверхности пластины граничные условия III-рода:
на поверхности пластины граничные условия III-рода: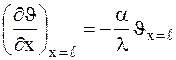 .
. . (9.5)
. (9.5) , (9.6)
, (9.6)  . (9.7)
. (9.7)


