
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охлаждение и нагревание неограниченной пластины. Частные случаиСодержание книги
Поиск на нашем сайте
Рассмотрим процесс охлаждения плоской стены (пластины), толщиной
Уравнение однородной стационарной теплопроводности (9.1) для рассматриваемого случая можно записать через избыточную температуру: Для решения этого уравнения необходимо иметь краевые условия. Начальные условия. 1) Граничные условия: так как плоскость симметрии пластины проходит через 2) При 3) при В соответствии с (9.2) общее решение (9.4) будет иметь вид: Используя начальные и граничные условия для определения постоянных интегрирования Уравнение (9.7) наиболее просто решается графически.
Из рисунка 9.3 видно, что имеется бесчисленное множество корней для каждого значения Bi. Найдём границы изменения числа Bi. Если Bi ® ¥, то при заданном размере стенки а корни уравнения (9.7) имеют следующие значения
На практике Если Bi ® 0, Þ a ® 0. В этом случае избыточная температура:
где n – порядковый номер корня. Для каждого значения 0 £ Bi £ ¥, решение дифференциального уравнения (9.4) будем искать в виде:
Определив
(быстросходящийся ряд Фурье) Решение (9.9) можно представить в обобщённых переменных:
где
Решения (9.10) представлены в виде простых и удобных номограмм, которые могут быть двух видов. Номограммы построены для двух случаев:
Зависимость (9.10) справедлива также для цилиндра и шара.
Для решения прямой задачи определения температуры в центре либо на поверхности пластины через какой-то момент времени после её охлаждения в среде с
В любом сечении температура находится с помощью решения (9.9). Частные случаи охлаждения (нагрева) неограниченной пластины Анализ решения дифференциального уравнения одномерной теплопроводности записанного для неограниченной пластины (9.9) в виде бесконечного, быстросходящегося ряда предполагает три характерных случая: 1)
Так как распределение температуры в теле определяется как внутренним термическим сопротивлением, так и внешним, то для инженерных расчётов при 2)
3)
Каждому значению числа Bi отвечает своя совокупность корней уравнения (9.9). Расход теплоты каждым м3 охлаждаемой пластины за время от
где С – теплоёмкость материала пластины; r – плотность пластины; J0 – начальная избыточная температура; `J – средняя избыточная температура по толщине пластины в момент t1. Числа теплового подобия Тепловое подобие – это подобие температурных полей и тепловых потоков Т.е. получили число подобия Фурье Это безразмерное время, которое характеризует временное развитие процесса теплопроводности (относительная форма текущего времени).
Pe выражает соотношение между переносом теплоты за счёт конвекции и за счёт молекулярной теплопроводности. Разделив Pe/Re получаем число Прандтля Pr:
Pr характеризует физические свойства среды, он табулирован в зависимости от температуры. Разделим
Nu характеризует интенсивность теплообмена на границе раздела тепловых сред и связывает интенсивность теплоотдачи a, и температурное поле l в пограничном слое потока. (13.8 – 13.11) – основные числа числового подобия. Дадим вспомогательные числа гидродинамического и теплового подобия. Комбинируя Re и Fr можно получить число подобия Галилея:
Комбинируя Ga с параметрическим числом, характеризующим неоднородное поле плотностей
Комбинируя Nu и Pe, получаем число подобия Стантона
St есть отношение конвективного теплового потока к тому тепловому потоку, который может быть перенесён потоком жидкости. При свободной конвекции Gr характеризует подъёмную силу, возникающую в жидкости вследствие разности плотностей (учёт свободной конвекции). Число подобия Маха – отношение скорости потока к местной скорости звука. где
М характеризует сжимаемость жидкости, если St пользуется при рассмотрении развитого турбулентного течения; Pr характеризует подобие полей скоростей и температуры в движущейся среде. Число подобия Релея: Ra представляет собой критерий тепловой неустойчивости или нестабильности при свободной конвекции. Число гомохромности или Струхаля: При изучении процессов гидродинамики и теплообмена могут встретиться следующие числа подобия. Число подобие Кирпичёва: (мера отношения потока тепла подводимой к поверхности тела, к потоку отводится с поверхности внутрь тела за счёт теплопроводности). Число подобия Кондратьева: (характеризует отставание изменения температуры какой-либо точки тела от изменения температуры окружающей среды, m – темп охлаждения). Число подобия Вебера: (критерий поверхности натяжения). We характеризует процесс дробления вязких жидкостей при распыле их воздухом или паром в горелочных устройствах. (отношение сил поверхностного натяжения к силам тяжести). где s – коэффициент поверхностного натяжения, Н/м; rк – плотность капли, кг/м3; r – плотность воздуха или пара, кг/м3;
Число подобия Лященко: (характеризует гидродинамическую обстановку в слое зернистого материала (кипящего слоя) при течении жидкости или газа сквозь слой твёрдого зернистого материала). Число подобия Стокса: характеризует процесс обтекания тел запылённым потоком газа. Является мерой отношения сил инерции и сил вязкости на движущуюся в потоке частицу. Всего обобщенных переменных в теории переноса порядка 140. Переходя от размерных физических величин или первичным к безразмерным комплексам или критериям, исходя из второй теоремы подобия, можно записать критериальные зависимости следующего вида:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.31.76 (0.009 с.) |

 .
.
 . (9.4)
. (9.4) ,
, 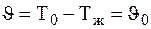 .
.  .
. , то
, то , при
, при  .
. на поверхности пластины граничные условия III-рода:
на поверхности пластины граничные условия III-рода: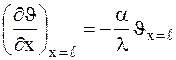 .
. . (9.5)
. (9.5) ,
,  можно получить трансцендентное уравнение вида:
можно получить трансцендентное уравнение вида:  , (9.6)
, (9.6)  . (9.7)
. (9.7)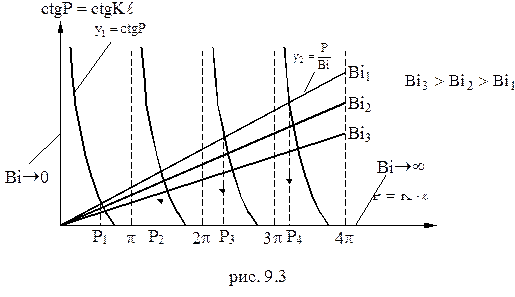
 и её материала, в этом случае a®¥; при этом температуры стенки и жидкости оказались равными
и её материала, в этом случае a®¥; при этом температуры стенки и жидкости оказались равными 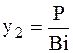 ,
, ;
;  ;
; 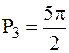 ; …;
; …;  ,
, .
. , это случай когда
, это случай когда  .
. , т.е. теплоотдачи от поверхности пластины к жидкости нет, и корни уравнения (9.7)
, т.е. теплоотдачи от поверхности пластины к жидкости нет, и корни уравнения (9.7) ,
, . (9.8)
. (9.8) , запишем окончательное решение уравнения теплопроводности (9.4):
, запишем окончательное решение уравнения теплопроводности (9.4): (9.9)
(9.9)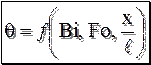 , (9.10)
, (9.10) – безразмерная координата;
– безразмерная координата;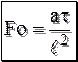 – число подобия Фурье (безразмерное время).
– число подобия Фурье (безразмерное время). – центр пластины
– центр пластины – поверхность пластины
– поверхность пластины
 , при заданных размерах
, при заданных размерах  . Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна:
. Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна: .
.
 в уравнении (9.9) можно ограничится первым членом ряда, так как термическое сопротивление
в уравнении (9.9) можно ограничится первым членом ряда, так как термическое сопротивление  , то температура на поверхности пластины становится равной температуре окружающей среды, т.е.
, то температура на поверхности пластины становится равной температуре окружающей среды, т.е.  .
. (
( ). Процесс выравнивания температуры в теле происходит значительно быстрее, чем отвод теплоты с поверхности пластины. Распределение температуры в этом случае показано на рисунке (9.7).
). Процесс выравнивания температуры в теле происходит значительно быстрее, чем отвод теплоты с поверхности пластины. Распределение температуры в этом случае показано на рисунке (9.7).
 (Реальный случай).
(Реальный случай).
 определяется по формуле:
определяется по формуле: ,
,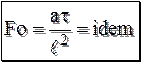 . (13.8)
. (13.8) – Число подобие Пекле
– Число подобие Пекле  , (13.9)
, (13.9)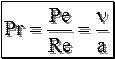 , (13.10)
, (13.10) – получим основное число теплового подобия числа Нуссельта Nu (безразмерный коэффициент теплоотдачи):
– получим основное число теплового подобия числа Нуссельта Nu (безразмерный коэффициент теплоотдачи): , (13.11)
, (13.11) . (13.12)
. (13.12) , получим число подобия Архимеда:
, получим число подобия Архимеда: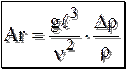 . (13.13)
. (13.13) . (13.14)
. (13.14) , где b – температурный коэффициент объёмного расширения. В результате из Ar получаем число Грасгофа Gr:
, где b – температурный коэффициент объёмного расширения. В результате из Ar получаем число Грасгофа Gr:  , (13.15)
, (13.15) , (13.16)
, (13.16) – для идеального газа,
– для идеального газа, – для реального газа.
– для реального газа. , то жидкость (газ) считаем несжимаемой;
, то жидкость (газ) считаем несжимаемой; . (13.17)
. (13.17) .
. .
. .
. .
. .
.




