
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоотдача при поперечном омывании пучка трубСодержание книги
Поиск на нашем сайте
Теплообменные поверхности выполняют из труб в виде пучков. Расположение труб в пучке может быть либо в коридорном, либо в шахматном порядках (рис 15.3).
В кожухотрубчатых теплообменниках может быть ромбическое или концентрическое расположение труб в пучке:
К характеристикам пучка относятся: – поперечный шаг пучка (S1) – расстояние между осями двух соседних труб в ряду, перпендикулярному движению жидкости; – продольный шаг пучка (S2) – расстояние между осями двух соседних труб в ряду, параллельному движению жидкости; – относительный поперечный шаг пучка – отношение S1/d; – относительный продольный шаг пучка – отношение S2/d; – количество рядов труб поперёк движения жидкости – n1; – количество рядов труб вдоль движения жидкости – n2; Т.к. пучок является турбулизатором потока, то критическое значение числа Рейнольдса Reкр для пучка будет равно:
Если Коэффициент теплоотдачи для первого ряда труб аналогичен коэффициенту теплоотдачи одиночной трубы. На теплоотдачу второго и последующих рядов влияет геометрия пучка (S1 и S2), поэтому первый ряд является турбулизатором для второго ряда, и коэффициент теплоотдачи у второго ряда будет больше. Начиная с третьего ряда коэффициент теплоотдачи устанавливается постоянным.
Для смешанного режима течения изменение коэффициента теплоотдачи по рядам показано на (рис. 15.4). Определяющий размер – наружный диаметр трубы. Определяющая скорость – скорость в самом узком месте. Определяющая температура – средняя температура теплоносителя. Коэффициент теплоотдачи для пучка труб определяется исходя из критериального уравнения для третьего и последующих рядов труб:
при Для коридорного расположения: Для шахматного расположения: Поправочный множитель ei для третьего и последующих рядов равен 1, а для первого и второго рядов определяется из рис 15.4. Коэффициент eS учитывает влияние относительности шагов. Для коридорного пучка Поправка Для очень вязких жидкостей ( Для полого многослойного цилиндра заданы: температуры горячей и холодной жидкостей ( Требуется найти: тепловой поток (Q) и линейную плотность теплового потока ( Аналогично как для плоской стенки линейная плотность теплового потока
Выразим из (4.10) разности температур и, сложив почленно эти три уравнения, получим: ,
Чтобы найти тепловой поток через цилиндрическую поверхность необходимо
(линейный коэффициент теплопередачи)
Величина обратная
Плотность теплового потока, отнесённая к внутренней поверхности цилиндра, обозначим через
где
Плотность теплового потока, отнесённая к внешней поверхности цилиндра, обозначим через
где
Связь между коэффициентами теплопередачи следующая:
Отсюда видно, что На практике, если отношение наружного диаметра цилиндра к внутреннему не более 1.8, то можно пользоваться формулой расчёта коэффициента теплопередачи через плоскую стенку
Тепловой поток для цилиндрической стенки рассчитывается:
В этом случае ошибка не превысит 4%. Если отношения диаметров больше 1.8, то следует использовать формулы для цилиндрической стенки. Изоляцию трубопроводов рассчитывают как плоскую стенку. Ошибку можно уменьшить, если в качестве рассчётной брать поверхность со стороны меньшего a. 1. Если 2. если 3. если Для многослойной цилиндрической стенки формула линейной плотности теплового потока имеет вид.
где n – число слоёв. Температура на границе раздела слоёв:
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1130; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.183.77 (0.009 с.) |


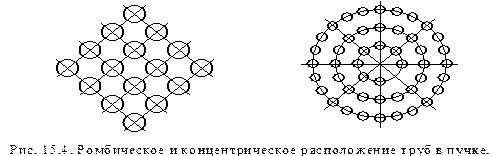
 .
. , то режим движения жидкости в пучке будет ламинарным; если
, то режим движения жидкости в пучке будет ламинарным; если  , то режим движения жидкости в пучке будет турбулентный; смешанный режим течения существует при условии
, то режим движения жидкости в пучке будет турбулентный; смешанный режим течения существует при условии  . Такой режим наблюдается в реальных теплообменных аппаратах.
. Такой режим наблюдается в реальных теплообменных аппаратах.
 ,
, .
. .
.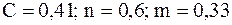 .
.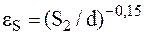 , для шахматного пучка
, для шахматного пучка  .
.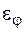 , учитывающая угол атаки j, выбирается из таблиц.
, учитывающая угол атаки j, выбирается из таблиц.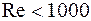 ):
): 
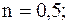
 . 31) Теплопередача через цилиндрическую стенку (при граничных условиях III-рода)
. 31) Теплопередача через цилиндрическую стенку (при граничных условиях III-рода) и
и  ), внутренний и внешний диаметры (
), внутренний и внешний диаметры ( и
и  ), коэффициент теплопроводности (
), коэффициент теплопроводности ( ), коэффициенты теплоотдачи (
), коэффициенты теплоотдачи ( и
и  ).
). ) при передаче теплоты через однослойную и многослойную стенки.
) при передаче теплоты через однослойную и многослойную стенки.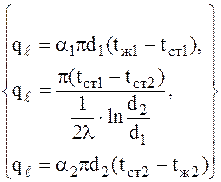 (4.10)
(4.10) ,
,  . (4.11)
. (4.11) ,
,  ,
,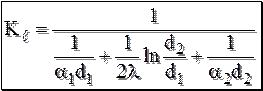 ,
, 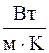 . (4.12)
. (4.12) – это количество теплоты, передаваемое в единицу времени через единицу длины цилиндрической поверхности от одной среды к другой при разности температур между средами в 1 градус.
– это количество теплоты, передаваемое в единицу времени через единицу длины цилиндрической поверхности от одной среды к другой при разности температур между средами в 1 градус. ,
,  . (4.12)
. (4.12) ,
, – коэффициент теплопередачи через цилиндрическую стенку, отнесённый к внутренней поверхности цилиндра.
– коэффициент теплопередачи через цилиндрическую стенку, отнесённый к внутренней поверхности цилиндра. ,
,  .
.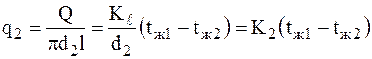 ,
, – коэффициент теплопередачи через цилиндрическую стенку, отнесённый к внешней поверхности цилиндра.
– коэффициент теплопередачи через цилиндрическую стенку, отнесённый к внешней поверхности цилиндра. .
. . (4.13)
. (4.13) всегда, т.к.
всегда, т.к.  .
.

 , Вт.
, Вт. , то
, то  ;
; , то
, то  ;
; , то
, то  .
. ,
, 


