
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность через шаровую стенкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Имеем полый шар с внутренним (
Для решения данного дифференциального уравнения второго порядка запишем граничные условия: при при Если температура меняется вдоль радиуса шара, то закон Фурье имеет вид:
Поверхность шара равна
После двойного интегрирования уравнения (5.1) и определения постоянных интегрирования получаем выражение для теплового потока через шаровую стенку
Плотность теплового потока через внутреннюю поверхность шара
Плотность теплового потока через наружную поверхность шара
Решением дифференциального уравнения (5.1) для температурного поля в шаровой стенке является
Подставляя в уравнение (5.5) радиус r в метрах, можно определить температуру t в любой точке шаровой поверхности. Изотермические поверхности в этом случае являются шаровыми, т.е. температура в шаровой стенке меняется по закону гиперболы. Для многослойной шаровой стенки из n-слоёв тепловой поток определяется из выражения:
Значения Гидромеханическое подобие конвективного теплообмена Найдём условия подобия двух потоков несжимаемой жидкости, которые описываются уравнением движения Навье-Стокса. Рассмотрим только уравнение движения для проекции скорости на ось Х:
Аналогично запишем для второй подобной системы (13.2) (всё с двумя штрихами). Вводим постоянные подобия (константы):
Выражаем уравнение движения Навье-Стокса для второй подобной системы через первую с учётом постоянных подобия
Из (13.3) выделим пять комплексов подобия:
 . .
Для получения числа подобия разделим второй комплекс на первый: Комплексы, составлены из констант подобия, когда справа или слева стоит 1, получили название индикатора подобия, заменяя в индикаторе подобия безразмерные константы подобия
где Но выражает меру переносного или конвективного ускорения к ускорению в данной точке. Разделив II на III получаем число подобия Фруда:
где Fr характеризует отношение инерционной силы в потоке к силе тяжести. Разделив IV на II, мы получаем число подобия Эйлера:
где Eu отношение перепада давления в потоке жидкости к динамическому давлению потока. Разделив II на V, получаем основное число гидромеханического подобия Рейнольдса Re:
где Re характеризует режим движения потока, и представляет собой меру отношения сил инерции к силам вязкости. Архимед, Галилей и Грасгоф являются производными числами подобия. Тепловое подобие Тепловое подобие – это подобие температурных полей и тепловых потоков. Рассмотрим две подобные системы (', "). Запишем уравнение энергии для одномерной задачи (температура меняется вдоль координаты Х), и уравнение теплообмена:
Введём постоянные подобия (константы). Константы подобия коэффициентов температуропроводности:
Заменяя переменные второй системы через переменные первой, мы получаем дифференциальное уравнение энергии и теплообмена для второй системы, записанное через переменные первой:
Уравнение теплообмена:
Выделим пять констант подобия:
 , ,
Разделим: Подставляя вместо постоянных подобия их размерные величины и произведя разделение переменных, мы получаем числа теплового подобия Т.е. получили число подобия Фурье Это безразмерное время, которое характеризует временное развитие процесса теплопроводности (относительная форма текущего времени).
Pe выражает соотношение между переносом теплоты за счёт конвекции и за счёт молекулярной теплопроводности. Разделив Pe/Re получаем число Прандтля Pr:
Pr характеризует физические свойства среды, он табулирован в зависимости от температуры. Разделим
Nu характеризует интенсивность теплообмена на границе раздела тепловых сред и связывает интенсивность теплоотдачи a, и температурное поле l в пограничном слое потока.
(13.8 – 13.11) – основные числа числового подобия. Дадим вспомогательные числа гидродинамического и теплового подобия. Комбинируя Re и Fr можно получить число подобия Галилея:
Комбинируя Ga с параметрическим числом, характеризующим неоднородное поле плотностей
Комбинируя Nu и Pe, получаем число подобия Стантона
St есть отношение конвективного теплового потока к тому тепловому потоку, который может быть перенесён потоком жидкости. При свободной конвекции Gr характеризует подъёмную силу, возникающую в жидкости вследствие разности плотностей (учёт свободной конвекции). Число подобия Маха – отношение скорости потока к местной скорости звука. где
М характеризует сжимаемость жидкости, если St пользуется при рассмотрении развитого турбулентного течения; Pr характеризует подобие полей скоростей и температуры в движущейся среде. Число подобия Релея: Ra представляет собой критерий тепловой неустойчивости или нестабильности при свободной конвекции. Число гомохромности или Струхаля: При изучении процессов гидродинамики и теплообмена могут встретиться следующие числа подобия. Число подобие Кирпичёва: (мера отношения потока тепла подводимой к поверхности тела, к потоку отводится с поверхности внутрь тела за счёт теплопроводности). Число подобия Кондратьева: (характеризует отставание изменения температуры какой-либо точки тела от изменения температуры окружающей среды, m – темп охлаждения). Число подобия Вебера: (критерий поверхности натяжения). We характеризует процесс дробления вязких жидкостей при распыле их воздухом или паром в горелочных устройствах. (отношение сил поверхностного натяжения к силам тяжести). где s – коэффициент поверхностного натяжения, Н/м; rк – плотность капли, кг/м3; r – плотность воздуха или пара, кг/м3;
Число подобия Лященко: (характеризует гидродинамическую обстановку в слое зернистого материала (кипящего слоя) при течении жидкости или газа сквозь слой твёрдого зернистого материала). Число подобия Стокса: характеризует процесс обтекания тел запылённым потоком газа. Является мерой отношения сил инерции и сил вязкости на движущуюся в потоке частицу. Всего обобщенных переменных в теории переноса порядка 140. Переходя от размерных физических величин или первичным к безразмерным комплексам или критериям, исходя из второй теоремы подобия, можно записать критериальные зависимости следующего вида:
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.212.14 (0.012 с.) |


 ) и внешним (
) и внешним ( ) радиусами и постоянным коэффициентом теплопроводности
) радиусами и постоянным коэффициентом теплопроводности  . Температура на внутренней поверхности –
. Температура на внутренней поверхности –  , а на внешней –
, а на внешней –  , причём
, причём 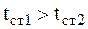 . Дифференциальное уравнение теплопроводности при стационарном режиме записывается в сферических координатах в виде (см. 2.11). Считаем, что температура меняется только вдоль радиуса r и не зависит от широты и долготы, поэтому дифференциальное уравнение теплопроводности преобразовывается в вид:
. Дифференциальное уравнение теплопроводности при стационарном режиме записывается в сферических координатах в виде (см. 2.11). Считаем, что температура меняется только вдоль радиуса r и не зависит от широты и долготы, поэтому дифференциальное уравнение теплопроводности преобразовывается в вид: . (5.1)
. (5.1) ,
, .
. , Вт.
, Вт. .
.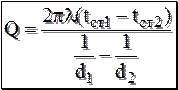 . (5.2)
. (5.2) ,
, 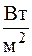 . (5.3)
. (5.3) ,
,  . (5.5)
. (5.5) . (5.6)
. (5.6) в (5.6) задаются.
в (5.6) задаются. (13.1)
(13.1) ;
;  ;
;  ;
;  ;
; ;
;  ;
;  .
. (13.3)
(13.3) .
. .
.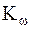 ,
,  ,
,  на размерные величины w, t,
на размерные величины w, t,  , получаем число подобия гомохронности или Струхаля:
, получаем число подобия гомохронности или Струхаля:  , (13.4)
, (13.4) , (13.5)
, (13.5) , (13.6)
, (13.6) , (13.7)
, (13.7) ,
, ,
,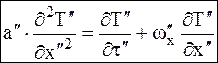 ,
, .
. ;
;  ;
;  ;
;  ;
;  .
. .
.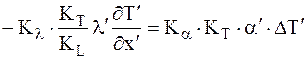 .
. .
.
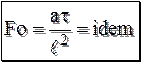 . (13.8)
. (13.8) – Число подобие Пекле
– Число подобие Пекле  , (13.9)
, (13.9)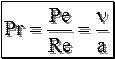 , (13.10)
, (13.10) – получим основное число теплового подобия числа Нуссельта Nu (безразмерный коэффициент теплоотдачи):
– получим основное число теплового подобия числа Нуссельта Nu (безразмерный коэффициент теплоотдачи): , (13.11)
, (13.11) . (13.12)
. (13.12) , получим число подобия Архимеда:
, получим число подобия Архимеда: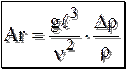 . (13.13)
. (13.13) . (13.14)
. (13.14) , где b – температурный коэффициент объёмного расширения. В результате из Ar получаем число Грасгофа Gr:
, где b – температурный коэффициент объёмного расширения. В результате из Ar получаем число Грасгофа Gr:  , (13.15)
, (13.15) , (13.16)
, (13.16) – для идеального газа,
– для идеального газа, – для реального газа.
– для реального газа. , то жидкость (газ) считаем несжимаемой;
, то жидкость (газ) считаем несжимаемой; . (13.17)
. (13.17) .
. .
. .
. .
. .
.




