
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетика ионных токов через биологическую мембрануСодержание книги Поиск на нашем сайте
Потенциал действия Все клетки возбудимых тканей при действии раздражителей достаточной силы переходят в состояние возбуждения. К возбудимым тканям относят: нервную, мышечную, железистую ткани. Возбудимость – способность клеток к быстрому ответу на раздражение, проявляющуюся через совокупность физической, физико-химической и функциональных изменений. Основная особенность (обязательное условие) – изменение электрического состояния клеточной мембраны. Потенциал действия – общее изменение разности потенциалов между цитоплазмой клетки и внешней средой, происходящее при пороговом и сверхпороговом возбуждении.
Возбуждение клетки связано с кратковременным увеличением теплопроводности клеточной мембраны: 1000 Ом/см2 ÷ 25 Ом/см2 (Т ↓ => теплопроводность увеличивается) Причина изменения – резкое изменение по Na+. Развитие потенциала действия сопровождается сначала утратой, а потом уменьшенный в течении некоторого времени способности мембраны к возбуждению – рефрактерность (невпечатлительность)
Кинетика ионных токов через биологическую мембрану
Уравнение, описывающее изменение ионов тока во времени (характер этого изменения), было предложено Ходкином и Хаксли. Они снимали потенциалостатические зависимости (потенциал поддерживается пост. = 0)
Раствор, омывающий аксон кальмара, заменили на не содержащий Na+ (граф. 2). Затем вычли из 1 2 => протекание только ионов Na+ (граф. 3).
Проводимость мембраны ~ токам.
Открытие ион. каналов, обеспечивающих перенос Na+, К+, обусловлено процессами активации (открытие) и инактивации (блокировка) каналов. Активация и инактивация является вероятностным процессом, описывается уравнением кинетики 1-го порядка.
С0 - общ. число каналов, способных пропускать ионы Na+ С – кол-во активированных каналов
Начальные условия: при t = 0 m=0 (все каналы не активированы)
При t →∞ при t →∞:
Обозначим m = m∞(1-℮-t/τ), (1) τ - постоянного времени Наибольшее соответствие происходит, когда ток Na описывается, если взять m3 (вместо m):
Аналогично для проводимости:
Ур-е, описывающее процесс инактивации, соответствующее участку б. Доля неинактивированных каналов (незаблокированных) = h, => 1-h = доля инактивированных каналов
Решение этого уравнения при t=0 h=h0: h=h∞(h∞- h0) ℮-t/τλ,
Аналогично для каналов К+, но процесс инактивации идёт очень медленно => рассмотрим только процесс активации:
n = n∞ - (n∞- n0) ℮-t/τλ
В итоге выделили 4 компонента тока, протекающего в мембране: 1. Ток смещения jсм = C 2. Ток ионов К+:
3. Ток ионов Na+:
4. Ток утечки, обусловленный движением через мембрану ионов
Ур-е полного тока через мембрану:
Глава 8. Электрокинетические явления К электрокинетическим явлениям относят: - движение фаз гетерогенной системы друг относительно друга при наложении на эту систему внешнего электрического поля; или возникновение электрического поля (разности потенциалов при движении фаз): - электрофорез, электроосмос, потенциалотечение, потенциалоседание. Дисперсная фаза – раздробленные частицы того или иного размера, находящиеся в сплошной непрерывной (дисперсионной) среде. Электрофорез Электрофорез – движение частицы дисперсной фазы дисперсионной системы в электрическом поле.
ε0– диэлектрическая проницаемость вакуума ε – относительная диэлектрическая проницаемость Е – напряженность электрического поля μ – динамическая вязкость дисперсионной среды
Высота поднятия частиц ~ ζ потенциалу
ζ потенциал электроцитов (рh = 7,4) ζ = 16,3 мВ Электроосмос
(+) частица проходит через пору, (-) отталкивается => уровень растворителя повышается. Высота зависит от подаваемого напряжения. При работе почек происходит это явление наряду с обычным осмосом. Костная ткань. 2/3 массы кости занимает гидроксилопатит: 3Са3(РО4)2 · Са(ОН)2 + коллаген. Механическая плотность костной ткани ρ = 2400 кг/см3. Е = 10 ГПа. σв = 150 МПа (предел прочности).
ОА – упругая деформация АВ – процесс ползучести ВС – упругая деформация при снятии нагрузки СД – обратная ползучесть Кожа. Состоит из коллагена (75% сухой массы) и 4% эластина (по свойствам похож на резину), а также жира и соединительной ткани. Эластин растягивается на 200-300%, коллаген на 10%.
Мышцы. В основном состоят из молекул миозина и актина. Мышцы делят на: - поперечно-полосатые; - гладкие. Гладкие мышцы образуют полые органы.
гладкие мышцы
являются поперечно-полосатыми. ε
Известен элемент, моделирующий упругие и пластичные свойства, - это пружина.
σ
В качестве модели вязкого тела используют поршень, передвигающегося в цилиндре.
σ
µ - коэффициент дин. вязкости. Деформацию, сочетающую вязкость и упругость, характерные для полимеров и биологических тканей, называют вязко-упругой.
Продифференцируем уравнение (1):
ε = εупр + εвязк,
1 случай: Пусть σ = σ0 = const Из (5) →
Интегрируем с начальными условиями: при t = 0
2 случай: Если ε = ε0 = const (напряжения будут релаксироваться)
НУ: при t = 0 σ0 = ε0Е Тогда lnC = lnσ0
2. Модель Фойгта (параллельное соединение).
В этом случае складываются не усилия, а перемещения. σ = σупр + σвяз (10) Пусть σ = σ0 = const Используя (1), (2) и (10):
ГУ: Пусть при t = 0, ε = 0.
Отсюда
ε σ0/Е ε1
t1 t σ
σ0
t
Из (13)
В соответствии с (11):
При t = t1, ε = ε1, тогда
→ или 3. Смешанная модель.
При движении постоянной нагрузки: ε
B
A C
O D t
ОА – упругая деформация пружины 1; АВ – вязко-упругая деформация двух параллельных соединенных пружин. В точке В σ = 0. σ
σ0
t ВС – упругая деформация пружины 1. СД – релаксация напряжений. Работа сердца Система кровообращения состоит из сердца и кровеносных сосудов, которые образуют большой и малый круги кровообращения.
Внутренний круг – временная шкала. Внутреннее кольцо – систола (заштрихована) и диастола предсердий. Наружное кольцо – систола и диастола желудочков.
Работу сердца разделяют на 2 вида: кинетическую и статическую. Статический компонент работы – работа по созданию давления, кинетический – по созданию скорости. Аст = Рср · Vc Рср – среднее давление, создаваемое сердцем. Vc – систолический (ударный) объем крови. График изменения давления
КД – кровяное давление.
Рср ≈ 100 мм.рт.ст ≈ 13,3 кПа – в большом круге из левого желудочка. Vс ≈ 70 мл. Из правого желудочка Рср ≈ 15 мм.рт.ст ≈ 2 кПа Астат.лев = 13,3 · 103 · 70 · 10-6 = 0,93 Д. Астат.прав = 2 · 103 · 70 · 10-6 = 0,14 Д. Основные понятия гемодинамики Различают линейную и объемную скорость.
V = l ∙ S, где S – сечение сосуда. Q = V ∙ S Чаще всего в сосудах реализуется ламинарное течение, переход из турбулентного оценивается критерием Re:
Reкр ≈ 970 ± 80 (т.к. кровь не подчиняется закону Ньютоновской жидкости).
τ– касательное напряжение между слоями жидкости. µ ≈ 10 сП – в мелких артериях. µ ≈ 800 сП – в капиллярах. Пульсовая волна Распространяющуюся по аорте и артериям волну повышения давления называют пульсовой волной. Скорость распространения 5-10 м/с.
р(о) = ро сonst Решение (14) и (15) имеет вид:
υ – скорость распределения волны β и a связаны соотношением (из этого решения):
Длина волны:
Получим приближенное выражение для β: R <<ДL для крупных сосудов, тогда ωRC ≈ 0. → a ≈ 0 Тогда из первого уравнения системы (17):
Газообмен в легких Газообмен между альвеолярной газовой смесью и кровью капилляров происходит через АКМ – альвеолярно-капиллярную мембрану. Активного переноса через АКМ нет, осуществляется только за счет диффузии.
Уравнение Фика:
l – толщина стенки АКМ.
В покое DΛО2 = 20-25; ДЛСО2 = 600 см3 мин-1мм.рт.ст. Парциальное давление О2 и СО2 в организме человека
Из формулы Фика:
§15.4. Транспорт газа в крови. Это вторая стадия дыхания. Транспорт О2 осуществляется двумя путями: 1) проникнув в тело, О2 растворяется в плазме крови (растворимость: 0,3 см3 на 100г крови), 2) 14-16г гемоглобина на 100г крови, а каждый грамм гемоглобина связывает 1,39см3 О2, поэтому в 100мл крови за счет связывания с гемоглобином пропорционально 20 см3 О2. Углекислый газ переносится за счет 1) растворения 2,4 см3 в 100 мл крови (5% всего СО2); 2) 15% СО2 кровь несет в виде карбогемоглобина
карбогемоглобин (реакция протекает вправо в тканях, влево – в легких) 3) 80% СО2 переносится за счет вытеснения О2 из гемоглобина (эффект Бора): СО2 + Н2О Н+ + HbO2 ↔ H + (Hb) + O2
Характеристики звука. Звук – колебание давления в какой-либо среде. Амплитуда колебаний давлений называется звуковым давлением (р, Па). Интенсивность звука – поток энергии звуковых волн, проходящих через единицу площади поверхности, перпендикулярной направлению распространения звуковых волн, в единицу времени (I, Вт/м2).
c – скорость звука в среде с плотностью ρ. Уровень интенсивности звука (L):
I0 – опорная интенсивность звука. Обычно берут минимальный порог звука I0 =10-12 Вт/м2. Если k =1, то [L] = Бел, если k =10, то [L] = децибел. Порог болевой чувствительности: I = 10 Вт/м2.
Потенциал действия Все клетки возбудимых тканей при действии раздражителей достаточной силы переходят в состояние возбуждения. К возбудимым тканям относят: нервную, мышечную, железистую ткани. Возбудимость – способность клеток к быстрому ответу на раздражение, проявляющуюся через совокупность физической, физико-химической и функциональных изменений. Основная особенность (обязательное условие) – изменение электрического состояния клеточной мембраны. Потенциал действия – общее изменение разности потенциалов между цитоплазмой клетки и внешней средой, происходящее при пороговом и сверхпороговом возбуждении.
Возбуждение клетки связано с кратковременным увеличением теплопроводности клеточной мембраны: 1000 Ом/см2 ÷ 25 Ом/см2 (Т ↓ => теплопроводность увеличивается) Причина изменения – резкое изменение по Na+. Развитие потенциала действия сопровождается сначала утратой, а потом уменьшенный в течении некоторого времени способности мембраны к возбуждению – рефрактерность (невпечатлительность)
Кинетика ионных токов через биологическую мембрану
Уравнение, описывающее изменение ионов тока во времени (характер этого изменения), было предложено Ходкином и Хаксли. Они снимали потенциалостатические зависимости (потенциал поддерживается пост. = 0)
Раствор, омывающий аксон кальмара, заменили на не содержащий Na+ (граф. 2). Затем вычли из 1 2 => протекание только ионов Na+ (граф. 3).
Проводимость мембраны ~ токам.
Открытие ион. каналов, обеспечивающих перенос Na+, К+, обусловлено процессами активации (открытие) и инактивации (блокировка) каналов. Активация и инактивация является вероятностным процессом, описывается уравнением кинетики 1-го порядка.
С0 - общ. число каналов, способных пропускать ионы Na+ С – кол-во активированных каналов
Начальные условия: при t = 0 m=0 (все каналы не активированы)
При t →∞ при t →∞:
Обозначим m = m∞(1-℮-t/τ), (1) τ - постоянного времени Наибольшее соответствие происходит, когда ток Na описывается, если взять m3 (вместо m):
Аналогично для проводимости:
Ур-е, описывающее процесс инактивации, соответствующее участку б. Доля неинактивированных каналов (незаблокированных) = h, => 1-h = доля инактивированных каналов
Решение этого уравнения при t=0 h=h0: h=h∞(h∞- h0) ℮-t/τλ,
Аналогично для каналов К+, но процесс инактивации идёт очень медленно => рассмотрим только процесс активации:
n = n∞ - (n∞- n0) ℮-t/τλ
В итоге выделили 4 компонента тока, протекающего в мембране: 1. Ток смещения jсм = C 2. Ток ионов К+:
3. Ток ионов Na+:
4. Ток утечки, обусловленный движением через мембрану ионов
Ур-е полного тока через мембрану:
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.187 (0.009 с.) |

 Потенциал действия не зависит от величины возбуждения, если оно выше порогового (если ниже – возбуждения не происходит). – этот принцип называется законом «всё или ничего».
Потенциал действия не зависит от величины возбуждения, если оно выше порогового (если ниже – возбуждения не происходит). – этот принцип называется законом «всё или ничего».



 => N = N0℮-λt (ур-е кинетики)
=> N = N0℮-λt (ур-е кинетики) (уравнение кинетики 1-го порядка, обусловлено активацией каналов)
(уравнение кинетики 1-го порядка, обусловлено активацией каналов)








 =>
=> jNa+ = jNa+m3, jNa+ - плотность тока по Na+ при доле актив. каналов = m
jNa+ = jNa+m3, jNa+ - плотность тока по Na+ при доле актив. каналов = m jNa+ - плотность тока ионов Na+ при активировании всех каналов
jNa+ - плотность тока ионов Na+ при активировании всех каналов q Na+ = q Na+ m3 (соотв-т участку а)
q Na+ = q Na+ m3 (соотв-т участку а)


 q К+ = q К + n4, n- доля активированных калиевых каналов.
q К+ = q К + n4, n- доля активированных калиевых каналов.

 C – электрическая ёмкость мембраны.
C – электрическая ёмкость мембраны. (уравнение Ходкина- Хаксли)
(уравнение Ходкина- Хаксли) (формула Смолуховского)
(формула Смолуховского) ζ – потенциал практически измерить очень трудно => уравнение служит для расчета потенциала
ζ – потенциал практически измерить очень трудно => уравнение служит для расчета потенциала Электроосмос – движение дисперсионной среды (жидкости) дисперсионной системы в электрическом поле.
Электроосмос – движение дисперсионной среды (жидкости) дисперсионной системы в электрическом поле.
 σ скелетная мышца
σ скелетная мышца Скелетная мышца и сердечная мышца
Скелетная мышца и сердечная мышца § 13.2. Моделирование механических свойств биологических объектов
§ 13.2. Моделирование механических свойств биологических объектов
 - закон Гука.
- закон Гука.
 - закон вязкого сопротивления
- закон вязкого сопротивления 1. Модель Максвелла (заключается в том, что 2 элемента соединяются последовательно) (соответствуют гладкие мышцы).
1. Модель Максвелла (заключается в том, что 2 элемента соединяются последовательно) (соответствуют гладкие мышцы).

 (3) + (4):
(3) + (4):















 или
или 
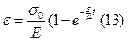















 , где ∆t = t2 – t1.
, где ∆t = t2 – t1. - линейная скорость.
- линейная скорость. , м3/с – объемная скорость.
, м3/с – объемная скорость.

 - закон Ньютона (для крови µ изменяется).
- закон Ньютона (для крови µ изменяется).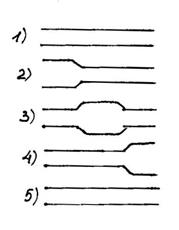
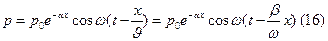
 (17)
(17)


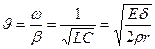 (19)
(19)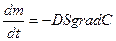 (8)
(8) (9)
(9)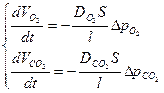 (10)
(10) (11)
(11)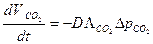
 - дифференциальная способность легких по О2.
- дифференциальная способность легких по О2.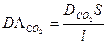 - дифференциальная способность легких по СО2.
- дифференциальная способность легких по СО2.

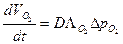
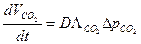

 Hb – NH2 + CO2 ↔ Hb – NH – COOH ↔ Hb – N – COO - + H+
Hb – NH2 + CO2 ↔ Hb – NH – COOH ↔ Hb – N – COO - + H+ Н2СО3 ↔ Н+ + НСО3- (атом Н+ вытесняет О2)
Н2СО3 ↔ Н+ + НСО3- (атом Н+ вытесняет О2) , (1)
, (1) , (2)
, (2)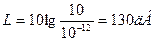 (20-30 дБ соответствуют шепоту, 80 дБ - крику).
(20-30 дБ соответствуют шепоту, 80 дБ - крику).


