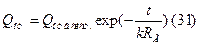Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетический компонент работыСодержание книги Поиск на нашем сайте
υ = 0,7 м/с.
(ρкрови = 1,05 г/см3) А = 0,14 + 2 · 0,02 + 0,93 = 1,11 = 1,2 Д А – суммарная работа. Мощность сердца:
Основные понятия гемодинамики Различают линейную и объемную скорость.
V = l ∙ S, где S – сечение сосуда. Q = V ∙ S Чаще всего в сосудах реализуется ламинарное течение, переход из турбулентного оценивается критерием Re:
Reкр ≈ 970 ± 80 (т.к. кровь не подчиняется закону Ньютоновской жидкости).
τ– касательное напряжение между слоями жидкости. µ ≈ 10 сП – в мелких артериях. µ ≈ 800 сП – в капиллярах. Уравнение деформации кровеносных сосудов
Р – давление. σт – тангенциальные напряжения в стенке сосуда. r – радиус сосуда.
2r ∙ l ∙ p = 2δ ∙ l ∙ σт (2δ ∙ l) – площадь продольного сечения стенки сосуда.
Меняется и δ, и r, но объем стенок сосуда постоянный V = 2πrδl = const rδ = α 0 = const
Из (2) и (3) →
Если использовать S = πr2, dS = 2πrdr, то
Оценка показывает, что второе слагаемое меньше, чем первое
Уравнения движения и изменения давления во времени крови в сосуде При ламинарном стационарном течении крови в цилиндрическом канале:
Изменение давления затрачивается на преодоление трения о стенки сосудов; будем считать, что при движении крови в сосудах толчками на преодоление сил трения затрачивается то же изменение давления dp. На преодоление сил вязкого трения нужна сила:
Сила, необходимая для сообщения ускорения
Складываем (8) и (9), обозначаем dp = dpвязк + dpинерц, делим на S, dx:
Изменение объема крови в элементе dx равно изменению объема, который вошло и который вышло, за время dt. dS∙dx = Q1dt – Q2dt = -(Q2 – Q1) dt = -dQdt. dS∙dx – изменение объема.
Разделим (7) на dt:
Подставим (11) в (12):
Система уравнений (10) – (13) отражает взаимную зависимость давления и объем. скорости кровотока во времени и по длине сосуда. Эластичная цепь как аналоговая модель кровеносной системы
Роль напряжения играет давление p, роль тока – объемная скорость Q. Пульсовая волна Распространяющуюся по аорте и артериям волну повышения давления называют пульсовой волной. Скорость распространения 5-10 м/с.
р(о) = ро сonst Решение (14) и (15) имеет вид:
υ – скорость распределения волны β и a связаны соотношением (из этого решения):
Длина волны:
Получим приближенное выражение для β: R <<ДL для крупных сосудов, тогда ωRC ≈ 0. → a ≈ 0 Тогда из первого уравнения системы (17):
Резестивная модель периферического кровообращения
где Rг= При последовательном соединении сосудов Rг складывается, т.е. R=R1+R2 +…+Rn, а при параллельном Rг зависит от того участка, на котором его рассматривают:
1 – аорта 2 – магистральные артерии 3 – артериолы 4 – капилляры 5 – вены
График изменения кровяного давления в большом круге кровообращения:
Пульсовое давление ≈ 40 мм.рт.ст. Рс – систолическое давление. Рд – диастолическое давление. 1 – аорта 2 – крупные артерии 3 – мелкие артерии 4 – артериолы 5 – капилляры 6 – венулы 7 – вены 8 – полые вены Гидродинамическая модель кровообращения с сосредоточенными параметрами
УР – упругий резервуар.
Уравнение баланса объема крови:
(объем крови идет на увеличение объема емкости УР и на Qот). V – объем УР. V = V0 + kр, (23) V0 – объем при р = 0, k – коэффициент пропускаемости.
рв ≈ 0 Подставим (24), (25) в (22):
Проинтегрируем (27) в пределах периода изменения давления:
Vс – объем, выброс крови за одно сокращение.
Во время диастолы Q = 0 (кровь из сердца в аорту не поступает). (26) будет иметь вид:
рс – систолическое давление при t = 0. Поделим обе части (30) на RГ → получим объем скорость кровотока:
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.14 (0.008 с.) |

 ≈ 0,02 Д
≈ 0,02 Д
 - линейная скорость.
- линейная скорость. , м3/с – объемная скорость.
, м3/с – объемная скорость.

 - закон Ньютона (для крови µ изменяется).
- закон Ньютона (для крови µ изменяется).
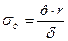 - уравнение Ламе
- уравнение Ламе
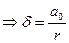
 (1)
(1) (2)
(2)




 (4)
(4) (5)
(5) (6)
(6)
 (уравнение Пуазеля)
(уравнение Пуазеля)


 элементу объема крови Sdx, где
элементу объема крови Sdx, где  - средняя скорость.
- средняя скорость.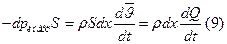
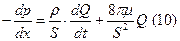


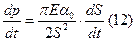

 - сопротивление трению
- сопротивление трению - емкость сосуда, связанная с эластичностью
- емкость сосуда, связанная с эластичностью - индуктивность
- индуктивность


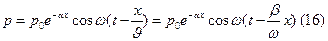
 (17)
(17)


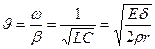 (19)
(19)
 , где ∆ρ – перепад давления на длине l.
, где ∆ρ – перепад давления на длине l.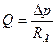 , (21)
, (21) (гемодинамическое сопротивление)
(гемодинамическое сопротивление)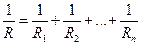 .
.

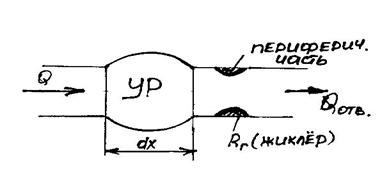 Артериальная часть кровообращения моделируется резервуаром:
Артериальная часть кровообращения моделируется резервуаром:

 , где рв – давление в венах.
, где рв – давление в венах.



 ,
,  ,
, 
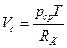

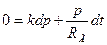 , разделяя переменные:
, разделяя переменные:
 ,
,