
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Охлаждение и нагревание неограниченной пластиныСодержание книги
Поиск на нашем сайте
Рассмотрим процесс охлаждения плоской стены (пластины), толщиной
Уравнение однородной стационарной теплопроводности (9.1) для рассматриваемого случая можно записать через избыточную температуру: Для решения этого уравнения необходимо иметь краевые условия. Начальные условия. 1) Граничные условия: так как плоскость симметрии пластины проходит через 2) При 3) при В соответствии с (9.2) общее решение (9.4) будет иметь вид: Используя начальные и граничные условия для определения постоянных интегрирования Уравнение (9.7) наиболее просто решается графически.
Из рисунка 9.3 видно, что имеется бесчисленное множество корней для каждого значения Bi. Найдём границы изменения числа Bi. Если Bi ® ¥, то при заданном размере стенки а корни уравнения (9.7) имеют следующие значения
На практике Если Bi ® 0, Þ a ® 0. В этом случае избыточная температура:
где n – порядковый номер корня. Для каждого значения 0 £ Bi £ ¥, решение дифференциального уравнения (9.4) будем искать в виде:
Определив
(быстросходящийся ряд Фурье) Решение (9.9) можно представить в обобщённых переменных:
где
Решения (9.10) представлены в виде простых и удобных номограмм, которые могут быть двух видов. Номограммы построены для двух случаев:
Зависимость (9.10) справедлива также для цилиндра и шара.
Для решения прямой задачи определения температуры в центре либо на поверхности пластины через какой-то момент времени после её охлаждения в среде с
В любом сечении температура находится с помощью решения (9.9). 81 Теория подобия – это теория подобных явлений. Из геометрии известно, что треугольники подобны, если их углы равны, а стороны пропорциональны. В теории подобия размерные величины – скорость, время заменяются безразмерными комплексами, т.е. числами подобия. Теория подобия рассматривает такие условия, когда результат модельных экспериментов можно с достоверностью перенести на действующие установки.
Подобие систем определяют теоремы подобия: 1) физические процессы подобные друг другу имеют одинаковую физическую природу и описываются одинаковыми по форме записи дифференциальными уравнениями; 2) (основная теорема подобия) у подобных явлений условия однозначности одинаковые, а числа подобия получаются из условия однозначности равными между собой (имеют одинаковое числовое значение); 3) решения дифференциального уравнения, выражающие сущность данного физического процесса, можно представить в виде функциональной зависимости между числами подобия
83) Конвективный теплообмен Основные положения Конвекция возможна только в текучей среде, в которой перенос теплоты связан с переносом самой среды. Конвективный теплообмен – это совместный перенос теплоты за счёт теплопроводности и конвекции. Конвекция – это перенос теплоты при перемещении жидкости или газа в пространстве с одной температурой в пространство с другой температурой. Если в единицу времени через единицу контрольной поверхности перпендикулярно к ней проходит масса жидкости,
где w – скорость жидкости, м/с; r – плотность жидкости, кг/м3, то с ней переносится плотность теплового потока конвекцией.
где h – удельная энтальпия жидкости, Конвекция теплоты сопровождается теплопроводностью, так как при движении жидкости или газа происходит соприкосновение отдельных частиц, имеющих различные температуры. Поэтому конвективный теплообмен описывается уравнением:
уравнение конвективного теплообмена. Основное уравнением конвективного теплообмена – это уравнение теплоотдачи Ньютона-Рихмана.
a – количество теплоты, воспринимаемое единицей поверхности в единицу времени при разности температур
Средний коэффициент теплоотдачи:
(локальное значение коэффициента теплоотдачи) Экспериментально установлено, что коэффициент теплоотдачи a зависит от вида теплообмена и теплофизических свойств теплоносителя. В общем случае:
Все реальные жидкости и газы обладают вязкостью между слоями, движущимися с различными скоростями. Между этими слоями возникает сила внутреннего трения, которая противодействует движению (направлена в сторону, противоположную движению). Согласно закону Ньютона, эта касательная сила (S или t), отнесенная к единице поверхности, действует в плоскости, ориентированной по течению прямо пропорционально изменению скорости в направлении к нормали к этой плоскости:
где m – коэффициент пропорциональности – динамический коэффициент вязкости, Па×с; n – направление, перпендикулярное направлению движения.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.38 (0.006 с.) |

 .
.
 . (9.4)
. (9.4) ,
, 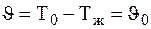 .
.  .
. , то
, то , при
, при  .
. на поверхности пластины граничные условия III-рода:
на поверхности пластины граничные условия III-рода: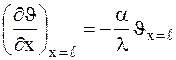 .
. . (9.5)
. (9.5) ,
,  можно получить трансцендентное уравнение вида:
можно получить трансцендентное уравнение вида:  , (9.6)
, (9.6)  . (9.7)
. (9.7)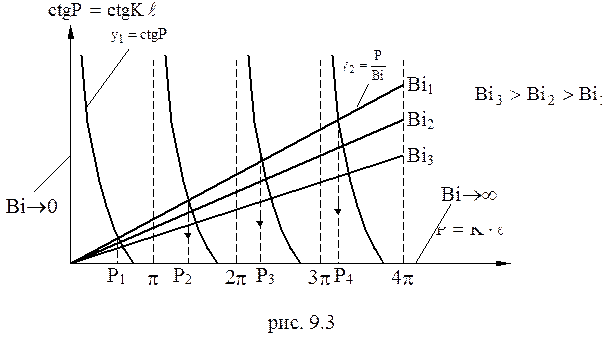
 и её материала, в этом случае a®¥; при этом температуры стенки и жидкости оказались равными
и её материала, в этом случае a®¥; при этом температуры стенки и жидкости оказались равными 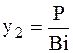 ,
, ;
;  ;
; 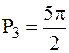 ; …;
; …;  ,
, .
. , это случай когда
, это случай когда  .
. , т.е. теплоотдачи от поверхности пластины к жидкости нет, и корни уравнения (9.7)
, т.е. теплоотдачи от поверхности пластины к жидкости нет, и корни уравнения (9.7) ,
, . (9.8)
. (9.8) , запишем окончательное решение уравнения теплопроводности (9.4):
, запишем окончательное решение уравнения теплопроводности (9.4): (9.9)
(9.9)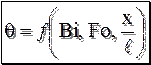 , (9.10)
, (9.10) – безразмерная координата;
– безразмерная координата;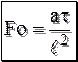 – число подобия Фурье (безразмерное время).
– число подобия Фурье (безразмерное время). – центр пластины
– центр пластины – поверхность пластины
– поверхность пластины
 , при заданных размерах
, при заданных размерах  . Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна:
. Поднимаем до пересечения с нужным Bi и находим относительную избыточную температуру, тогда абсолютная температура в центре будет равна: .
. ,
,  ,
,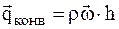 ,
, 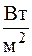 ,
, .
. (11.1)
(11.1)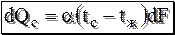 , (11.2)
, (11.2) ,
,  .
.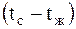 равной 1 градусу.
равной 1 градусу. .
. . (11.3)
. (11.3) , (11.4)
, (11.4)


