
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопередача через многослойную плоскую стенку при граничных условиях III-родаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пусть заданы температуры сред
Аналогично формуле (3.9) записывают уравнение сохранения плотности теплового потока q, выражая разность температур и складывая почленно полученные выражения плотности теплового потока
Коэффициент теплопередачи:
Из уравнения (3.16), определяя плотность теплового потока, находим температуры на поверхностях стенки Уравнение сплошности (или неразрывности) потока В основе вывода дифференциального уравнения неразрывности лежит закон сохранения массы: сколько массы втекает в объём, столько же должно и вытекать.
Элемент объёма жидкости (dx, dy, dz) располагается в произвольной точке пространства с координатами (x, y, z) и движется вдоль линии тока со скоростью w, проекции которой на оси будут равны wx, wy, wz. Состояние жидкости и свойство переноса в точке (x, y, z) обозначаем через Т, р, r, m. Пусть плотность жидкости будет постоянной ( Массовый расход жидкости вдоль оси Х через единицу площади будет равен Массовый расход жидкости через левую грань элементарного объёма будет равен Разность массовых расходов жидкости через две перпендикулярные оси Х грани или скорость накопления массы в элементе (dx, dy, dz) будет равна
Аналогично для осей Y и Z:
При условии постоянной плотности ( Т.к. (дифференциальное уравнение сплошности потока для несжимаемой жидкости) В векторной форме уравнение сплошности (неразрывности) записывается как Для сжимаемой жидкости (т.е. для жидкости с переменной плотностью) разность между скоростью прихода массы в элемент и скоростью ухода массы из элемента равна скорости накапливания массы элементом объёма.
(уравнение неразрывности для сжимаемой жидкости) В векторной форме:
Избыток массы обуславливается изменением плотности жидкости в объёме, равен изменению массы данного объёма во времени. 3) Различают три режима: 1) Ламинарное течение в пограничном слое:
2) Переходный режим (лобовая часть трубы омывается ламинарным пограничным слоем, а кормовая – турбулентным пограничным слоем):
3)Развитый турбулентный режим течения жидкости в пограничном слое:
При значении числа Рейнольдса Теплопроводность через цилиндрическую стенку (при граничных Условиях I-рода.) Ось OZ совмещаем с осью цилиндра, и температура меняется только вдоль радиуса цилиндра.
Для полого цилиндра заданы: внешний ( Требуется найти: уравнение, описывающее температурное поле в цилиндре, т.е. изменение температуры в зависимости от диаметра d (рад. r), а также плотность теплового потока q и сам тепловой поток Q. На основании дифференциального уравнения теплопроводности при стационарном режиме и отсутствии внутренних источников теплоты (2.10), учитывая, что первая и вторая производные температуры по z равны нулю
а также то, что температура не зависит от полярного угла j, то уравнение Лапласа в цилиндрических координатах (2.10) упрощается до вида
Граничные условия дифференциального уравнения: при при Введём новую переменную
тогда дифференциальное уравнение (4.1) будет иметь вид:
Интегрируем данное выражение:
Тогда, потенциируя это выражение и переходя к первоначальным переменным мы получаем:
После интегрирования получаем:
Для определения постоянных интегрирования
Решая уравнение (а) относительно
Подставляя в (4.2) значения
Это решение описывает распределение температуры в цилиндрической стенке. Это логарифмическая кривая (рис. 4.1). Задавая произвольным диаметр, можно определить температуру в любой точке цилиндрической поверхности. Согласно закону Фурье плотность теплового потока пропорциональна градиенту температуры (температура меняется только вдоль радиуса):
Из этого выражения следует, что тепловой поток полностью определяется внутренним и наружным диаметрами цилиндра ( Тепловой поток может быть отнесён к единице длины цилиндра
Тепловой поток может быть отнесён к внутренней поверхности цилиндра
Тепловой поток, отнесённый к наружной поверхности цилиндра
Связь между различными приведёнными плотностями теплового потока следующая
Следовательно, в отличие от плоской стенки плотность теплового потока непостоянна по толщине цилиндрической стенки и определяется текущим диаметром цилиндра (чем больше текущий диаметр, тем меньше плотность теплового потока). Если коэффициент теплопроводности не является величиной постоянной, а зависит от температуры по зависимости
Подставляемые в выражение (4.9) значения 29) Уравнение движения (уравнение Навье-Стокса)
Для вывода уравнения движения используют закон сохранения количества движения. Закон сохранения количества движения – изменение количества движения в элементе объёма жидкости (dx, dy, dz) равно результирующей всех внешних сил, приложенных к поверхности и объёму элемента.
Полная или субстанционная производная оценивает действительное ускорение, которое испытывает частица материи или субстанции проходя вдоль линии тока в поле скорости (рис. 11.1). Полная субстанционная производная для составляющей скорости вдоль оси ОХ будет равна
Аналогично для
(11.11) получаем уравнение движения для несжимаемой жидкости или уравнение Навье-Стокса:
где В векторной форме окончательное уравнение движения (или уравнение Навье-Стокса) для движущейся жидкости в гравитационном поле имеет вид:
Уравнение Навье-Стокса подтверждает второй закон Ньютона: произведение массы на ускорение равно сумме сил. Т.е. уравнение баланса количества движения соответствует второму закону Ньютона. Для частного случая, когда силами вязкого трения можно пренебречь для идеальной жидкости, уравнение Навье-Стокса превращается в уравнение Эйлера
Из (11.14) для установившегося безвихревого движения в поле силы тяжести энергетический баланс для элементарной струи жидкости описывается уравнением Бернулли:
Уравнение Навье-Стокса (11.12) определяет характер распределения скоростей в однородном потоке с постоянной скоростью. Если заданы краевые условия, начальные и граничные, то 4 уравнения сплошности (11.8) и уравнение движения (11.12) дают распределение в пространстве и во времени 4-х величин: wx, wy, wz, р. Эти распределения являются решением конкретной задачи. Чтобы найти поле распределения температур или энтальпий рассмотрим уравнение энергии
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

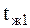 и
и  , коэффициенты теплоотдачи
, коэффициенты теплоотдачи  и
и  (закон теплообмена), коэффициенты теплопроводности
(закон теплообмена), коэффициенты теплопроводности 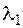 ,
,  и
и  , толщина слоёв стенки
, толщина слоёв стенки  ,
,  и
и  .
.
 ,
, 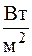 , (3.16)
, (3.16) ,
, 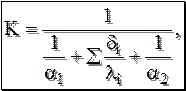
 (3.18)
(3.18)
 (3.19)
(3.19) ,
,  и температуры на границах слоёв
и температуры на границах слоёв  ,
,  .
.
 ), тогда масса жидкости в объёме (dx, dy, dz) должна сохраняться постоянной как при стационарном (скорость не изменяется во времени), так и при нестационарном режимах течения. Результирующий массовый расход жидкости через шесть граней должен быть равен нулю.
), тогда масса жидкости в объёме (dx, dy, dz) должна сохраняться постоянной как при стационарном (скорость не изменяется во времени), так и при нестационарном режимах течения. Результирующий массовый расход жидкости через шесть граней должен быть равен нулю. ,
,  .
.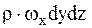 ,
,  .
. .
. ,
,  .
.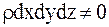 , то, следовательно,
, то, следовательно, 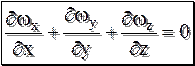 . (11.5)
. (11.5) . (11.6)
. (11.6) . (11.7)
. (11.7) . (11.8)
. (11.8)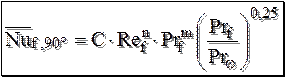 . (15.2)
. (15.2) .
. .
.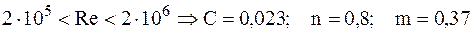 .
.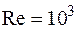 происходит изменение закона теплообмена. Уравнение (15.2) справедливо при угле атаки
происходит изменение закона теплообмена. Уравнение (15.2) справедливо при угле атаки  .
.
 ) и внутренний (
) и внутренний ( ) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок (
) радиусы, коэффициент теплопроводности (l), температуры холодной и горячей стенок (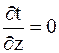 ,
,  ,
, . (4.1)
. (4.1)
 ;
;
 .
. ,
, .
. .
. .
.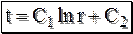 . (4.2)
. (4.2) и
и  воспользуемся граничными условиями:
воспользуемся граничными условиями: (а)
(а) , (б)
, (б) , (с)
, (с) . (4.3)
. (4.3) ;
; , Вт. (4.4)
, Вт. (4.4) и
и  ).
). ,
,  . (4.5)
. (4.5) (линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины
(линейная плотность теплового потока) – это количество теплоты, проходящее через цилиндрическую поверхность путём теплопроводности через единицу длины
 ,
, 
 ,
,  , (4.8)
, (4.8) , т.к.
, т.к.  .
.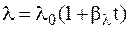 , то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения
, то температурное поле, т.е. линии изменения температуры в цилиндрической стенке, на любом диаметре может быть определено из следующего выражения . (4.9)
. (4.9) и
и  берутся из справочников.
берутся из справочников.
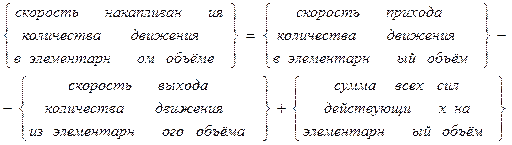
 . (11.9)
. (11.9) и
и  .
. , (11.9)
, (11.9)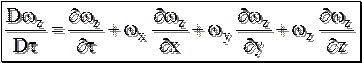 . (11.9)
. (11.9) (11.12)
(11.12) –проекции вектора ускорения свободного падения на оси.
–проекции вектора ускорения свободного падения на оси.
 ,
,  (11.13)
(11.13) . (11.14)
. (11.14)
 ,
,  (11.15)
(11.15)


