
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пограничный слой. Уравнения пограничного слоя. Отрыв пограничного слоя от стенки.Содержание книги
Поиск на нашем сайте
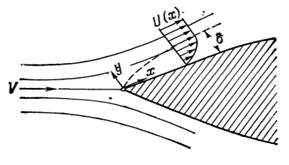
Пограничный слой. Уравнения пограничного слоя. Отрыв пограничного слоя от стенки. Критерии отрыва для ламинарных и турбулентных течений в пограничном слое. Потери полного давления на обтекаемой поверхности. OТРЫВ ПОГРАНИЧНОГО СЛОЯ ПРИ ОБТЕКАНИИ ТВЕРДЫХ ПОВЕРХНОСТЕЙ ГАЗОДИНАМИЧЕСКИМ ПОТОКОМ В 1904 г. Л. Прандтль в своем докладе «О движении жидкости при очень малом трении», прочитанном на математическом конгрессе в Гейдельберге, указал путь, сделавший доступным теоретическому исследованию течения жидкости с трением в практически важных случаях. А именно, исходя из теоретических соображений и некоторых простых экспериментов, Л. Прандтль показал, что течение в окрестности тела можно разделить на две области: на область очень тонкого слоя вблизи тела (пограничный слой), где трение играет существенную роль, и на область вне этого слоя, где трением можно пренебрегать. Эта гипотеза, с одной стороны, позволила получить физически очень наглядное объяснение важной роли вязкости в проблеме сопротивления, а с другой стороны, дала возможность преодолеть математические трудности и тем самым открыла путь теоретическому исследованию течений жидкости с трением. Плоское течение около тонкого клина при очень малой вязкости среды (очень большое число Рейнольдса)
Обозначим величины: u -продольная скорость(вдоль оси х); v- поперечная скорость (вдоль оси у); U- скорость внешнего потока; V- скорость набегающего потока; δ- толщина пограничного слоя; L- характерный линейный размер тела В течении будем рассматривать 2 области: — Первая область - очень тонкий слой в непосредственной близости от тела. В этой области градиент скорости ∂u/∂y в направлении, перпендикулярном к стенке, очень велик, а вязкость μ оказывает существенное влияние на течение, поскольку здесь касательное напряжение τ= μ ∂u/∂y, вызванное трением, может принимать большие значения — Вторая область-все остальное течение вне пограничного слоя. В этой области градиент скорости не достигает таких больших значений, как в пограничном слое, поэтому действие вязкости здесь не играет роли и можно считать, что течение здесь потенциальное. Запишем уравнения Навье-Стокса в безразмерной форме, для этого: — все скорости отнесем к скорости V набегающего потока; — все длины –к характерному линейному размеру тела L,который выберем так, чтобы безразмерная величина ∂u/∂x в рассматриваемой области течения не превышала по порядку единицу; — давление и время разделим соответственно на ρV2 и на L/V; — введем число РейнольдсаRe=VL/ν
Критерии отрыва пограничного слоя: Параметры, определяющие течение: • U – скорость; • ρ – плотность; • Р – давление внешнего потока в сечении х*; • Р́х(х*); • z- характерный размер пограничного слоя, • μ – характерная constвязкости; • λ – const теплопроводности; • γ – отношение теплоёмкостей. Характерным линейным размером пограничного слоя может быть δ, δ*, δ** и др. - толщина вытеснения
- толщина потери импульса
По теореме размерностей все безразмерные величины есть функции только безразмерных комбинаций определяющих параметров
В точке отрыва пограничного слоя τ=0, т.е Ф=0, следовательно, соотношение (11) можно разрешить относительно параметра
В ламинарном пограничном слое при μ→0, Re→∞, z→0.
T.к. φ0(М) не стремится к 0 при μ→0, то для ламинарного пограничного слоя φ0(М) ≡0. Умножая обе части равенства (12) на ρUz/μ и переходя к пределу при Re→∞, получим, что в точке отрыва ламинарного пограничного слоя справедливо соотношение:
В случае турбулентного пограничного слоя при μ→0 характерный размер пограничного слоя z не стремится к 0 (т.к.толщина пограничного слоя определяется турбулентным перемешиванием). Следовательно, не стремится к 0 и Р́хz/ρU2. Поэтому в случае турбулентного пограничного слоя φ0(М)≠0. Все остальные члены в (12) содержат Re-1. Устремляя μ→0 (Re→∞), получим для турбулентного пограничного слоя над точкой отрыва соотношение:
Методы очистки газовых потоков от посторонних частиц и капель воды. Инерционные газоочистители (ИГ). Назначение ИГ. Постановка задачи о течении в каналах ИГ.
Методы очистки газовых потоков от посторонних частиц и капель воды Для улавливания из газов твёрдых и жидких примесей, в промышленности применяют механический, электрический способы очистки газов. Механическую очистку газов производят осаждением частиц примесей под действием силы тяжести или центробежной силы, фильтрацией сквозь волокнистые и пористые материалы, промывкой газа водой или др. жидкостью. Наиболее простым, но малоэффективным и редко применяемым является способ осаждения крупной пыли под действием силы тяжести в т. н. пылевых камерах. Инерционный способ осаждения частиц пыли (или капель жидкости) основан на изменении направления движения газа со взвешенными в нём частицами. Т. к. плотность частиц примерно в 1—3 тыс. раз больше плотности газа, они, продолжая двигаться по инерции в прежнем направлении, отделяются от газа
Инерционные газоочистители (ИГ). Назначение ИГ Инерционными уловителями пыли служат т. н. пылевые мешки, жалюзийные решётки, зигзагообразные отделители, каналы сложной формы и т.п. В некоторых аппаратах используется и сила удара частиц. Для очистки газов широко применяют Циклоны, в которых отделение от газа твёрдых и жидких частиц происходит под действием центробежной силы (при вращении газового потока). Т. к. центробежная сила во много раз превосходит силу тяжести, в циклонах осаждается и сравнительно мелкая пыль, с размером частиц примерно 10—20 мкм и до ≈80 мкм
Постановка задачи о течении в каналах ИГ При изучении газодинамического течения в канале будем пользоваться предположением о том, что объемная концентрация посторонних частиц в потоке мала ( Будем считать газ невязким, нетеплопроводным, движение установившимся плоским или осесимметричным. Течение газа в каналах и примыкающих к ним устройствах стремятся сделать такими, чтобы энергетические потери потока были минимальны. Стенки таких каналов делают гладкими, стремясь избежать резких изменений площади поперечного сечения канала, чтобы не вызвать отрыва потока от стенки. Поэтому вязкие эффекты в каналах такого рода проявляются в основном вблизи стенок и могут быть учтены отдельно с использованием теории пограничного слоя. В основной массе газа вязкие эффекты можно не учитывать, т.е. считать газ идеальным. При моделировании движения частиц записываются уравнения движения центра масс отдельной частицы с учетом воздействий различных сил: аэродинамического сопротивления, силы веса, архимедовой силы и т.д. Взаимодействием между частицами пренебрегается. Дисперсный состав частиц может быть любым. Рассматриваются частицы с линейным размером d от 2 до 1000 мкм. Диапазон изменения размеров может лимитироваться только временем счета каждой отдельной задачи. Модель учитывает взаимодействие частиц со стенками канала. Рассматриваются различные законы рикошета.
В потоке газа. По предположению объемная концентрация пыли в потоке мала, и поэтому можно считать, что частицы не взаимодействуют между собой и рассчитывать траектории их движения, пользуясь уравнением для одной частицы. Запишем дифференциальное уравнение движения центра массы частицы
Здесь Частица считается сферической. Коэффициент присоединенной массы учитывает результирующую аэродинамических сил, зависящих от ускорения частицы. При потенциальном безотрывном обтекании частицы величина Реально Величина
где
Сила аэродинамического сопротивления для сферических частиц направлена против скорости
где n- кинематическая вязкость, а – скорость звука в газе,
Одним из важнейших элементов исследования движения газа с твердыми частицами является определение взаимодействия газ – частица, где проявляются свойства вязкости и теплопроводности несущей среды, даже в том случае, когда среда считается идеальной. Вопросу сопротивления при движении твердых частиц в вязкой среде уделяется внимание во всех работах, связанных с движением гетерогенных сред в разнообразных условиях. Правильное описание движения смеси существенно зависит от достоверных данных по коэффициенту сопротивления В основном, большинство теоретических и экспериментальных исследований относится к определению коэффициента сопротивления твердой сферы в потоке вязкой несжимаемой жидкости [см.например,72,75,76,86,87]. Поле течения при обтекании сферы равномерным потоком вязкой несжимаемой жидкости было впервые изучено Стоксом путем интегрирования уравнений Навье – Стокса при пренебрежении инерционными членами и с использованием условий прилипания жидкости на всей поверхности сферы. Выражение для коэффициента сопротивления, которое обычно называют законом Стокса, имеет вид
В дальнейшем это выражение было уточнено Озееном, который частично учел инерционные члены и получил
Уточнение Гольдштейна, полученное путем разложения в ряд, дает значение коэффициента сопротивления с более высокими степенями чисел Рейнольдса
Праудмен и Пирсон дали другое обобщение формулы для
Необходимо отметить, что наряду с теоретическими проводились и экспериментальные исследования с шариками из различных материалов, движущихся в несжимаемых средах. Обобщение экспериментов и осредненная кривая для При возрастании чисел Рейнольдса (Re>1) обтекание сферы вязким потоком качественно меняется. Пограничный слой в кормовой части сферы отрывается с образованием вихревой зоны и следа. В широком диапазоне чисел Re влияние сил вязкости и инерции значительно во всем поле течения, поэтому возможности аналитического исследования уменьшаются и данные по коэффициенту сопротивления и характеру обтекания можно получить либо экспериментально, либо путем численного решения уравнений Навье – Стокса. При различных условиях эксперимента получаются различные значения чисел Re, при которых начинается отрыв потока. Считается, что отрыв возникает при Re~10. По мере увеличения числа Re величина отрывной зоны растет. При Re@100 система вихрей и отрывная зона распространяются на расстояние около одного диаметра от задней части сферы. При Re~130-150 отрывная зона начинает колебаться, а при Re~700 вихревые кольца поочередно срываются с противоположных сторон сферы и уносятся в след. Число Re, при котором начинается срыв вихрей в след, называется нижним критическим числом Рейнольдса (Re Разные авторы дают различные значения Re При Re>Re При числах Re от 2 Это явление объясняется переходом ламинарного пограничного слоя на поверхности сферы в турбулентный, при этом точка отрыва на сфере смещается вниз по течению, возникает более узкий вихревой след и сопротивление сферы уменьшается. В работах [87, 114] дается обзор и анализ экспериментальных исследований по сопротивлению сфер, проведенных разными авторами. Несмотря на значительный разброс экспериментальных данных удалось обобщить их в так называемой стандартной кривой, описывающей зависимость Сложный характер не позволяет описать
где A и n=const, которые достаточно точно аппроксимируют эту величину. При этом пренебрегается отличием формы частицы от сферической, шероховатостью поверхности, дроблением и коагуляцией частиц, их вращением, турбулентностью потока и изменением при неустановившемся движении среды. Эксперименты показали, что влияние всех этих факторов незначительно и не превышает 6 - 10% [74,75]. Аппроксимация экспериментальных зависимостей
Существенное влияние на величину Как и в случае несжимаемой жидкости получена стандартная кривая зависимости При малых дозвуковых скоростях значение коэффициента сопротивления соответствует несжимаемой жидкости. С ростом числа Маха При 1.5£М£2.0 коэффициент сопротивления достигает максимального значения Авторы [1], обобщая экспериментальные данные, приведенные в [97] при Re=200 -
где В дальнейшем, при расчетах конкретных течений полидисперсной среды, будет использоваться формула (19) при малых числах М в относительном движении газ – частица или формула (20) при М³0.2. Приведем в заключение этого пункта некоторые соображения, связанные с учетом вращения частиц. При малых числах Re захват среды при вращении частицы увеличивает скорость потока на одной стороне тела и уменьшает на другой. Возникает эффект Магнуса, т.е. сила, направленная в сторону большей скорости обтекания. Однако, при отрыве потока точки отрыва будут перемещаться по поверхности сферы, вызывая силу противоположную силе Магнуса. Результаты ряда экспериментальных и теоретических работ [83] показывают, что вращение частицы не изменяет существенно коэффициента сопротивления. Можно показать, что во многих случаях остальные силы, действующие на частицу, малы по сравнению с Архимедова сила мала, т.к. мало Пример:
Силы взаимодействия между частицами также малы, если частиц в потоке мало; можно пренебречь также силой термофореза, которая возникает в потоке с неравномерной температурой газовой среды. Эта сила мала по сравнению с Со стенкой канала.
При достижении твердой частицей поверхности, ограничивающей канал, возникает явление рикошета вследствие удара частицы о стенку. Вопросу взаимодействия различных частиц с твердой поверхностью посвящено большое число работ (см. например, [74,99,109,113,115,118]). В данном исследовании нас будут интересовать изменения скорости твердой частицы после отскока от стенки. Имеется ряд экспериментальных работ, где показано, что закон изменения скорости частицы после столкновения со стенкой существенно зависит от материалов стенки и частицы [99,115]. Необходимо отметить, что теоретические и экспериментальные исследования в этой области дают значительно различающиеся результаты.

Рис.2. Схема рикошета частиц от стенки.
Рассмотрим это явление в прямоугольной системе координат х, у. Будем пренебрегать возможным разрушением частицы при ударе. Пусть D плоскость, проходящая через вектор скорости частицы в момент ее соприкосновения со стенкой и нормаль к стенке канала в этой точке. Спроектируем скорость частицы на нормаль и на касательную к стенке в плоскости D. Обозначим скорость частицы до и после удара о стенку через Тогда закон отражения частицы от стенки можно записать в виде
Коэффициенты
Здесь Величины На рис.3,4 представлены коэффициенты По оси абсцисс отложен угол Необходимо отметить, что частицы различного происхождения имеют форму, отличную от сферической. Форма частицы сказывается на характере движения, если размер ее не слишком мал. Установлено, что в достаточно большом диапазоне размеров частиц (от 2 до 1000 мк) введением коэффициента формы
Рис. 3. Зависимость коэффициента
Рис. 4. Зависимость коэффициента
Модель турбулентности В безразмерном виде система уравнений во вращающейся цилиндрической системе координат имеет вид:
где
Здесь dn расстояние вдоль нормали до стенки. Значения констант, входящих в последние формулы, следующие:
Начальные условия: Начальными условиями задачи являются заданные в момент времени t=0 приближенные распределения гидродинамических параметров по всему рабочему пространству ступени насоса. Эти распределения могут вычисляться либо из решения одномерной задачи для моделируемого режима работы насоса, либо задаваться простейшим образом (например, полное отсутствие движения флюида в ступени в момент запуска насоса). Необходимым условием решения задачи является задание полной 3D геометрии всей проточной части.
Граничные условия: Граничные условия задачи: · на неподвижных стенках все компоненты скорости задаются равными нулю – условие прилипания, · на подвижных стенках скорость · на входе в насос задаются полные параметры набегающего потока, а также направление скорости; · на выходе - статическое давление окружающей среды. Другой вариант задания граничного условия на входе состоит в задании расхода флюида вместо полного давления. Такой подход дает более устойчивое решение, поэтому при проведении расчетов для надежности получаемых результатов моделировались параллельно два решения (на разных ПК) и проводилось их сравнение.
Исходные данные: Численный эксперимент проводился для ступени электроцентробежной погружной насосной установки для нефтедобычи - ЭЦН АКМ. Параметры расчета: · Рабочее тело – вода: плотность ρ = 997 кг/м3, вязкость m = 0.001003 кг/м×с, температура Т = 300 К. · Рассматривается изотермический процесс. · Частота вращения ротора насоса: ω = 10000 об/мин. В результате расчетов обнаружены существенные различия в характере течения при малых и больших расходах через ступень. В связи с этим анализ результатов будет приведен для двух предельных значений расходов, при которых проводился численный эксперимент: 30 м3/сут и 160 м3/сут.
Интегральные характеристики: Пограничный слой. Уравнения пограничного слоя. Отрыв пограничного слоя от стенки.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.152.168 (0.013 с.) |




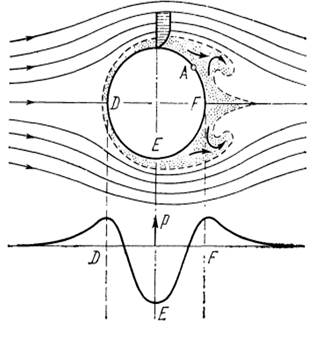
 Схематическое изображение отрыва пограничного слоя и образования вихрей при обтекании круглого цилиндра; А-точка отрыва.
Схематическое изображение отрыва пограничного слоя и образования вихрей при обтекании круглого цилиндра; А-точка отрыва.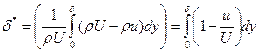
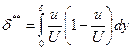
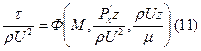
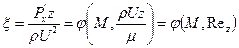
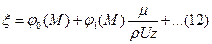 Разложим функцию φ по 1/Rez:
Разложим функцию φ по 1/Rez: Совершим предельный переход μ→0.
Совершим предельный переход μ→0.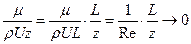 Известно, что z/L~(Re)-1/2 (Re=ρUL/μ), следовательно
Известно, что z/L~(Re)-1/2 (Re=ρUL/μ), следовательно
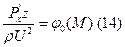
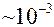 ), в связи с чем газодинамическое течение будем рассматривать независимо от движения частиц, считая их влияние на поток пренебрежимо малым.
), в связи с чем газодинамическое течение будем рассматривать независимо от движения частиц, считая их влияние на поток пренебрежимо малым.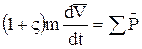 ,
, 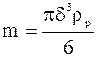 (17)
(17) - коэффициент присоединенной массы, m - масса твердой частицы,
- коэффициент присоединенной массы, m - масса твердой частицы, 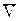 - вектор абсолютной скорости частицы,
- вектор абсолютной скорости частицы,  - сумма векторов сил, действующих на частицу,
- сумма векторов сил, действующих на частицу, 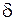 - линейный размер частицы,
- линейный размер частицы, 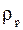 - ее плотность.
- ее плотность.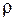 (m /
(m / 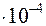 , например для частиц кварца, поэтому величиной
, например для частиц кварца, поэтому величиной 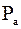 +
+ 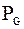 +
+ 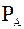 +
+ 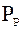
 - сила аэродинамического сопротивления;
- сила аэродинамического сопротивления;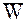 - ее движения относительно газа, и может быть записана в виде
- ее движения относительно газа, и может быть записана в виде (18)
(18)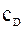 - коэффициент сопротивления,
- коэффициент сопротивления, 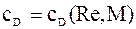 ,
, 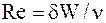 ,
,  ,
, 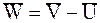 .
.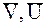 - абсолютные скорости частицы и газа.
- абсолютные скорости частицы и газа.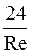 (1*)
(1*)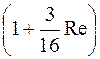
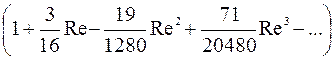 (2*)
(2*)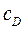 в виде
в виде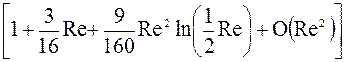 (3*)
(3*) ).
).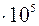 до 4
до 4  ~1…5
~1…5  , (19)
, (19)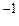

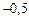
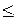 0.6
0.6
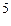
 и М=0.2 – 0.98, предложили аппроксимацию для коэффициента сопротивления в виде
и М=0.2 – 0.98, предложили аппроксимацию для коэффициента сопротивления в виде (20)
(20)
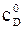 - одна из аппроксимаций стандартной кривой
- одна из аппроксимаций стандартной кривой  , сила тяжести мала, т.к. малы массы частиц.
, сила тяжести мала, т.к. малы массы частиц.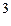 ,
, 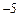 м, W=1м/c,
м, W=1м/c, 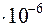 м
м  /c, то
/c, то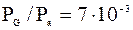 ,
, 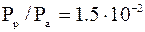 при gradP = 50Па/мм.
при gradP = 50Па/мм.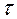
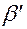

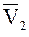
 и
и 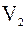 соответственно, а проекции на нормаль и касательную пометим индексами n и t. Считая поверхность частицы и стенки гладкими можно принять, что после удара касательная составляющая скорости сохраняет свое первоначальное направление, а нормальная составляющая меняет направление на противоположное (см. рис.2).
соответственно, а проекции на нормаль и касательную пометим индексами n и t. Считая поверхность частицы и стенки гладкими можно принять, что после удара касательная составляющая скорости сохраняет свое первоначальное направление, а нормальная составляющая меняет направление на противоположное (см. рис.2).
 ,
, 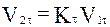 ,
, 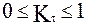 (21)
(21)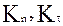 представляют собой коэффициенты восстановления импульса после удара и зависят от угла
представляют собой коэффициенты восстановления импульса после удара и зависят от угла 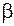 между вектором скорости
между вектором скорости  (22)
(22) - средние значения функций, полученных при обработке одного из экспериментов,
- средние значения функций, полученных при обработке одного из экспериментов, 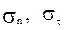 - соответствующие среднеквадратичные отклонения,
- соответствующие среднеквадратичные отклонения, 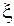 - случайная величина, распределенная по нормальному или по равномерному закону на отрезке
- случайная величина, распределенная по нормальному или по равномерному закону на отрезке 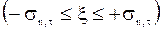 .
.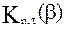 охватывают все детали случайного процесса, связанные с шероховатостью соприкасающихся поверхностей и отличием формы частицы от сферической. Учитывая случайные величины при отражении, логично предположить возникновение третьей составляющей скорости частицы после отскока ее от стенки, перпендикулярной к
охватывают все детали случайного процесса, связанные с шероховатостью соприкасающихся поверхностей и отличием формы частицы от сферической. Учитывая случайные величины при отражении, логично предположить возникновение третьей составляющей скорости частицы после отскока ее от стенки, перпендикулярной к 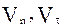 , которую представим в виде
, которую представим в виде 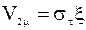 .
.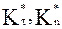 полученные в разных работах, в том числе и теоретические
полученные в разных работах, в том числе и теоретические 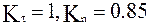 из [74] (под номером 5). Номером 6 помечен обобщенный закон для коэффициентов
из [74] (под номером 5). Номером 6 помечен обобщенный закон для коэффициентов 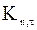 , выведенный в данной работе, как среднее значение всех других, что позволяет применять его для различных материалов стенок (алюминий, титан и др.) и частиц (кварц, графит и т.д.).
, выведенный в данной работе, как среднее значение всех других, что позволяет применять его для различных материалов стенок (алюминий, титан и др.) и частиц (кварц, графит и т.д.).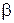 .
.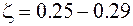 , на который умножается масса частицы в уравнениях движения, можно достичь хорошего согласования результатов расчета с экспериментальными данными [99].
, на который умножается масса частицы в уравнениях движения, можно достичь хорошего согласования результатов расчета с экспериментальными данными [99].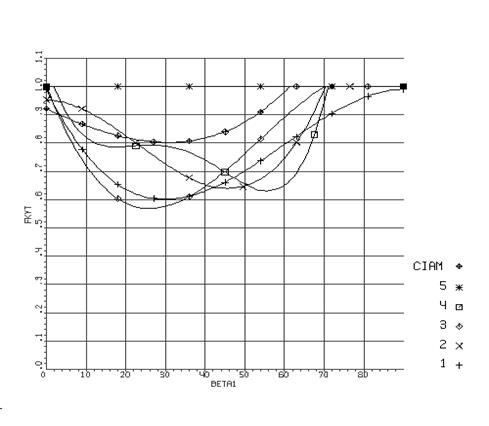
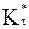 от угла
от угла 
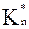 от угла
от угла 
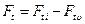



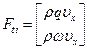



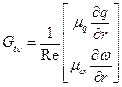

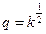

 - кинетическая энергия пульсаций
- кинетическая энергия пульсаций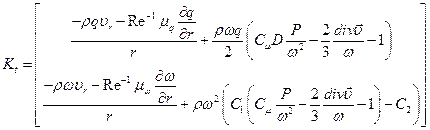
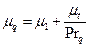
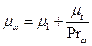
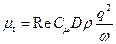
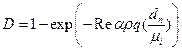
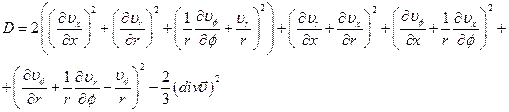
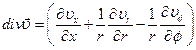
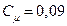
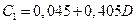
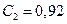
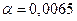


 = Ω, остальные компоненты скорости равны нулю;
= Ω, остальные компоненты скорости равны нулю;


