
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, можно принятьСодержание книги
Поиск на нашем сайте
Приведем полученную систему уравнений (21) к безразмерному виду. Для этого выберем систему характерных параметров, дополняющих систему (15). Примем Перепишем уравнения (19) с учетом (18) в безразмерных переменных, которые пометим звездочкой
где
Для построения траектории движения частицы запишем уравнения для определения координат движущейся по каналу частицы
Относя компоненты скорости частицы к Для интегрирования системы уравнений, определяющих движение частицы, необходимо задать начальные условия. Зададим при Таким образом, задача о движении твердой частицы в канале сводится к задаче Коши с начальными условиями для системы шести обыкновенных дифференциальных уравнений
t =0:
Законы рикошета частиц при столкновении Со стенкой канала.
При достижении твердой частицей поверхности, ограничивающей канал, возникает явление рикошета вследствие удара частицы о стенку. Вопросу взаимодействия различных частиц с твердой поверхностью посвящено большое число работ (см. например, [74,99,109,113,115,118]). В данном исследовании нас будут интересовать изменения скорости твердой частицы после отскока от стенки. Имеется ряд экспериментальных работ, где показано, что закон изменения скорости частицы после столкновения со стенкой существенно зависит от материалов стенки и частицы [99,115]. Необходимо отметить, что теоретические и экспериментальные исследования в этой области дают значительно различающиеся результаты.

Рис.2. Схема рикошета частиц от стенки.
Рассмотрим это явление в прямоугольной системе координат х, у. Будем пренебрегать возможным разрушением частицы при ударе. Пусть D плоскость, проходящая через вектор скорости частицы в момент ее соприкосновения со стенкой и нормаль к стенке канала в этой точке. Спроектируем скорость частицы на нормаль и на касательную к стенке в плоскости D. Обозначим скорость частицы до и после удара о стенку через Тогда закон отражения частицы от стенки можно записать в виде
Коэффициенты
Здесь Величины На рис.3,4 представлены коэффициенты По оси абсцисс отложен угол Необходимо отметить, что частицы различного происхождения имеют форму, отличную от сферической. Форма частицы сказывается на характере движения, если размер ее не слишком мал. Установлено, что в достаточно большом диапазоне размеров частиц (от 2 до 1000 мк) введением коэффициента формы
Рис. 3. Зависимость коэффициента
Рис. 4. Зависимость коэффициента
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 (21)
(21)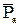 - сила аэродинамического сопротивления.
- сила аэродинамического сопротивления. ,
,  ,
,  , не конкретизируя их значения, за параметры, к которым будем относить плотность частиц, их размер и вязкость газа.
, не конкретизируя их значения, за параметры, к которым будем относить плотность частиц, их размер и вязкость газа.
 ;
;  ;
;  ;
;  ;
; - безразмерный критерий подобия.
- безразмерный критерий подобия. ,
, 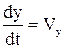 ,
, 
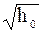 , координаты к характерному размеру L, а время к
, координаты к характерному размеру L, а время к  =0 во входном сечении канала начальные координаты частицы и ее скорость.
=0 во входном сечении канала начальные координаты частицы и ее скорость.
 ;
; 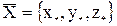
 =
= 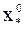 ,
,  ,
,  ,
,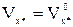 ,
,  ,
,  .
.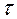
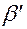

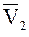
 и
и 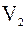 соответственно, а проекции на нормаль и касательную пометим индексами n и t. Считая поверхность частицы и стенки гладкими можно принять, что после удара касательная составляющая скорости сохраняет свое первоначальное направление, а нормальная составляющая меняет направление на противоположное (см. рис.2).
соответственно, а проекции на нормаль и касательную пометим индексами n и t. Считая поверхность частицы и стенки гладкими можно принять, что после удара касательная составляющая скорости сохраняет свое первоначальное направление, а нормальная составляющая меняет направление на противоположное (см. рис.2).
 ,
, 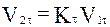 ,
, 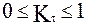 (21)
(21)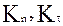 представляют собой коэффициенты восстановления импульса после удара и зависят от угла
представляют собой коэффициенты восстановления импульса после удара и зависят от угла 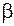 между вектором скорости
между вектором скорости  (22)
(22) - средние значения функций, полученных при обработке одного из экспериментов,
- средние значения функций, полученных при обработке одного из экспериментов, 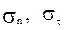 - соответствующие среднеквадратичные отклонения,
- соответствующие среднеквадратичные отклонения, 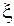 - случайная величина, распределенная по нормальному или по равномерному закону на отрезке
- случайная величина, распределенная по нормальному или по равномерному закону на отрезке 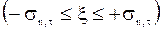 .
.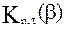 охватывают все детали случайного процесса, связанные с шероховатостью соприкасающихся поверхностей и отличием формы частицы от сферической. Учитывая случайные величины при отражении, логично предположить возникновение третьей составляющей скорости частицы после отскока ее от стенки, перпендикулярной к
охватывают все детали случайного процесса, связанные с шероховатостью соприкасающихся поверхностей и отличием формы частицы от сферической. Учитывая случайные величины при отражении, логично предположить возникновение третьей составляющей скорости частицы после отскока ее от стенки, перпендикулярной к 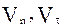 , которую представим в виде
, которую представим в виде 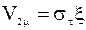 .
.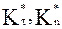 полученные в разных работах, в том числе и теоретические
полученные в разных работах, в том числе и теоретические 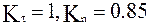 из [74] (под номером 5). Номером 6 помечен обобщенный закон для коэффициентов
из [74] (под номером 5). Номером 6 помечен обобщенный закон для коэффициентов 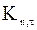 , выведенный в данной работе, как среднее значение всех других, что позволяет применять его для различных материалов стенок (алюминий, титан и др.) и частиц (кварц, графит и т.д.).
, выведенный в данной работе, как среднее значение всех других, что позволяет применять его для различных материалов стенок (алюминий, титан и др.) и частиц (кварц, графит и т.д.).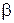 .
.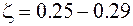 , на который умножается масса частицы в уравнениях движения, можно достичь хорошего согласования результатов расчета с экспериментальными данными [99].
, на который умножается масса частицы в уравнениях движения, можно достичь хорошего согласования результатов расчета с экспериментальными данными [99].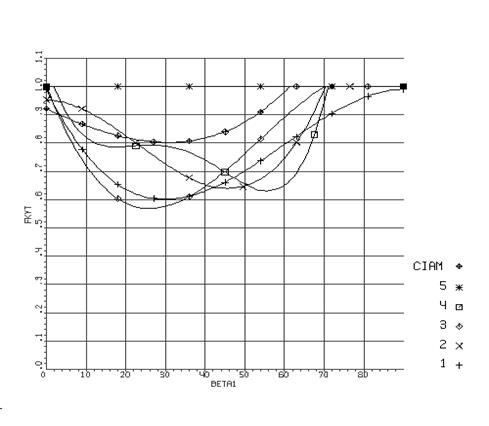
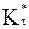 от угла
от угла 
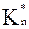 от угла
от угла 


