
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения движения газа в канале сложной геометрии. Методы решения. Критерии подобияСодержание книги
Поиск на нашем сайте
1. 2. Математическая модель течения газа в канале сложной геометрии.
Рассмотрим двумерное стационарное движение газа в канале заданной формы, которое описывается уравнениями неразрывности, импульсов и энергии [50], [85]. Уравнение неразрывности:
Уравнение импульсов в форме Лэмба-Громеки:
Уравнение энергии:
Спроектируем уравнение импульсов на линию тока, т.е. умножим скалярно на dx =
Здесь используются общепринятые обозначения:
Пусть на линии тока Lплотность и давление связаны зависимостью
Если Р Уравнение энергии (3) для адиабатических движений также дает интеграл вдоль линии тока
S(p,
Постоянные в (5) и (6) могут быть разными на разных линиях тока. Соотношение (6) позволяет вычислить интеграл (5), так как дает необходимую связь
Таким образом, вдоль линий тока установившихся непрерывных адиабатических течений сохраняются энтропия и полное теплосодержание газа. Если S(L) и Будем рассматривать плоские и осесимметричные незакрученные течения, все параметры которых зависят от х и у. Уравнение неразрывности запишем в виде
div(
В произвольной ортогональной системе координат для двумерного движения уравнение (8) выглядит так:
( Это уравнение можно рассматривать как условие существования полного дифференциала функции
Функция
Соотношение (11) определяет функцию тока любого течения с точностью до аддитивной постоянной;
Расход газа между двумя линиями тока равен разности значений функции тока на этих линиях. Будем рассматривать потенциальные течения, т.е.
что означает одновременно отсутствие вихря в течении. Из (11) найдем u и v
Тогда, используя условие потенциальности течения, получим
уравнение типа уравнения Лапласа, с переменными коэффициентами. Граничные условия сформулируем, пользуясь представлениями о расходе газа через канал, имеющий поворот и разветвление (рис.1). Обычно задается расход через входное сечение и расходы через две другие ветви - Между расходами выполняется очевидное соотношение:


 
 
Рис. 1. Форма канала и схема задания граничных условий для уравнений газовой динамики.
Значения Решая задачу (12) с заданными значениями
где Далее организуется итерационная процедура: по новому (13) распределению Полученное потенциальное течение служит фоном, на котором рассматривается движение твердых частиц, а также оно может быть использовано - для определения течения в пограничных слоях на стенках для расчета потерь полного давления; - в качестве начального приближения для решения задачи о нестационарном течении. Нестационарное течение также может представлять интерес в некоторых приложениях или использоваться для получения стационарного решения при Для получения решения методом установления уравнения газовой динамики записываются в форме законов сохранения
В декартовой системе координат уравнения газовой динамики имеют вид:
Здесь U(u,v) - вектор скорости движения газа с компонентами u, v,
для плоского случая -
Здесь
Система уравнений (14) решается методом установления по времени, подробно описанном в монографии [25]. Для удобства дальнейшего использования уравнений (12), (13) введем безразмерные переменные. Будем считать заданным характерный линейный размер канала L, расход газа
В безразмерных переменных уравнения (13) примут вид
Уравнение (12) в безразмерных переменных сохраняет свой вид. Безразмерный параметр Если при обезразмеривании уравнений (14) ввести те же переменные (15), а безразмерное время принять равным
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.53 (0.006 с.) |

 (1)
(1) (для установившихся течений)
(для установившихся течений) (2)
(2)
 (3)
(3) dt, тогда вдоль линии тока будем иметь
dt, тогда вдоль линии тока будем иметь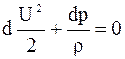 (4)
(4) - плотность, давление, скорость и энтропия газового потока.
- плотность, давление, скорость и энтропия газового потока. , тогда в области непрерывности движения уравнение (4) можно проинтегрировать и получить
, тогда в области непрерывности движения уравнение (4) можно проинтегрировать и получить (5)
(5) (L)=const, то интеграл Бернулли (5) дает связь между скоростью и давлением во всей области газа.
(L)=const, то интеграл Бернулли (5) дает связь между скоростью и давлением во всей области газа.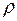 )=S(L) (6)
)=S(L) (6) (7)
(7) одинаковы на всех линиях тока, то движение – безвихревое [85], так как
одинаковы на всех линиях тока, то движение – безвихревое [85], так как  .
.
 (9)
(9) =1 для плоских,
=1 для плоских,  (10)
(10) (х,у) - функция тока, ее производные определяются выражениями
(х,у) - функция тока, ее производные определяются выражениями
 (11)
(11)
 ,
, 

 ,
, ;
; 
 +
+  =0 (12)
=0 (12) . Эти параметры определяют значения
. Эти параметры определяют значения 










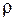 (х,у) известными численными методами, например [12,33] находим распределение u(х,у), v(х,у) и
(х,у) известными численными методами, например [12,33] находим распределение u(х,у), v(х,у) и  . Используя уравнение Бернулли и изэнтропичность течения, находим
. Используя уравнение Бернулли и изэнтропичность течения, находим
 (13)
(13)
 ,
,  -const, определяемые параметрами торможения газа на входе,
-const, определяемые параметрами торможения газа на входе,  - отношение теплоемкостей совершенного газа.
- отношение теплоемкостей совершенного газа. при других граничных условиях.
при других граничных условиях.
 (14)
(14) 

 ,
,  - внутренняя энергия газа,
- внутренняя энергия газа, - его плотность, p - давление; x, y- декартовы координаты, t – время,
- его плотность, p - давление; x, y- декартовы координаты, t – время,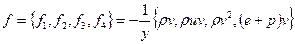 - для осесимметричного случая,
- для осесимметричного случая, .
. - полная энергия единицы объема,
- полная энергия единицы объема,  - внутренняя энергия единицы массы газа, определяемая уравнением состояния. Для совершенного газа
- внутренняя энергия единицы массы газа, определяемая уравнением состояния. Для совершенного газа .
. , а также параметры торможения газа - плотность
, а также параметры торможения газа - плотность  и энтальпию
и энтальпию 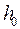 . Тогда, помечая безразмерные переменные звездочками, получим
. Тогда, помечая безразмерные переменные звездочками, получим ,
,  ,
,  ,
, 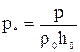
 ,
,  ,
,  ,
, 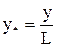 (15)
(15)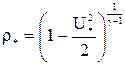
 (16)
(16) ,
, 
 является критерием подобия течения. Он аналогичен приведенной скорости.
является критерием подобия течения. Он аналогичен приведенной скорости. , то уравнения (14) в новых переменных сохранят свой вид.
, то уравнения (14) в новых переменных сохранят свой вид.


