
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения движения твердых частиц в газодинамическом потоке. Рикошет частиц от стенок канала. Методы решения. Критерии подобия. Критерии оптимальности ИГ. Теория и эксперимент.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математическая модель движения твердых частиц В потоке газа. По предположению объемная концентрация пыли в потоке мала, и поэтому можно считать, что частицы не взаимодействуют между собой и рассчитывать траектории их движения, пользуясь уравнением для одной частицы. Запишем дифференциальное уравнение движения центра массы частицы
Здесь Частица считается сферической. Коэффициент присоединенной массы учитывает результирующую аэродинамических сил, зависящих от ускорения частицы. При потенциальном безотрывном обтекании частицы величина Реально Величина
где
Сила аэродинамического сопротивления для сферических частиц направлена против скорости
где n- кинематическая вязкость, а – скорость звука в газе,
Одним из важнейших элементов исследования движения газа с твердыми частицами является определение взаимодействия газ – частица, где проявляются свойства вязкости и теплопроводности несущей среды, даже в том случае, когда среда считается идеальной. Вопросу сопротивления при движении твердых частиц в вязкой среде уделяется внимание во всех работах, связанных с движением гетерогенных сред в разнообразных условиях. Правильное описание движения смеси существенно зависит от достоверных данных по коэффициенту сопротивления В основном, большинство теоретических и экспериментальных исследований относится к определению коэффициента сопротивления твердой сферы в потоке вязкой несжимаемой жидкости [см.например,72,75,76,86,87]. Поле течения при обтекании сферы равномерным потоком вязкой несжимаемой жидкости было впервые изучено Стоксом путем интегрирования уравнений Навье – Стокса при пренебрежении инерционными членами и с использованием условий прилипания жидкости на всей поверхности сферы. Выражение для коэффициента сопротивления, которое обычно называют законом Стокса, имеет вид
В дальнейшем это выражение было уточнено Озееном, который частично учел инерционные члены и получил
Уточнение Гольдштейна, полученное путем разложения в ряд, дает значение коэффициента сопротивления с более высокими степенями чисел Рейнольдса
Праудмен и Пирсон дали другое обобщение формулы для
Необходимо отметить, что наряду с теоретическими проводились и экспериментальные исследования с шариками из различных материалов, движущихся в несжимаемых средах. Обобщение экспериментов и осредненная кривая для При возрастании чисел Рейнольдса (Re>1) обтекание сферы вязким потоком качественно меняется. Пограничный слой в кормовой части сферы отрывается с образованием вихревой зоны и следа. В широком диапазоне чисел Re влияние сил вязкости и инерции значительно во всем поле течения, поэтому возможности аналитического исследования уменьшаются и данные по коэффициенту сопротивления и характеру обтекания можно получить либо экспериментально, либо путем численного решения уравнений Навье – Стокса. При различных условиях эксперимента получаются различные значения чисел Re, при которых начинается отрыв потока. Считается, что отрыв возникает при Re~10. По мере увеличения числа Re величина отрывной зоны растет. При Re@100 система вихрей и отрывная зона распространяются на расстояние около одного диаметра от задней части сферы. При Re~130-150 отрывная зона начинает колебаться, а при Re~700 вихревые кольца поочередно срываются с противоположных сторон сферы и уносятся в след. Число Re, при котором начинается срыв вихрей в след, называется нижним критическим числом Рейнольдса (Re Разные авторы дают различные значения Re При Re>Re При числах Re от 2 Это явление объясняется переходом ламинарного пограничного слоя на поверхности сферы в турбулентный, при этом точка отрыва на сфере смещается вниз по течению, возникает более узкий вихревой след и сопротивление сферы уменьшается. В работах [87, 114] дается обзор и анализ экспериментальных исследований по сопротивлению сфер, проведенных разными авторами. Несмотря на значительный разброс экспериментальных данных удалось обобщить их в так называемой стандартной кривой, описывающей зависимость Сложный характер не позволяет описать
где A и n=const, которые достаточно точно аппроксимируют эту величину. При этом пренебрегается отличием формы частицы от сферической, шероховатостью поверхности, дроблением и коагуляцией частиц, их вращением, турбулентностью потока и изменением при неустановившемся движении среды. Эксперименты показали, что влияние всех этих факторов незначительно и не превышает 6 - 10% [74,75]. Аппроксимация экспериментальных зависимостей
Существенное влияние на величину Как и в случае несжимаемой жидкости получена стандартная кривая зависимости При малых дозвуковых скоростях значение коэффициента сопротивления соответствует несжимаемой жидкости. С ростом числа Маха При 1.5£М£2.0 коэффициент сопротивления достигает максимального значения Авторы [1], обобщая экспериментальные данные, приведенные в [97] при Re=200 -
где В дальнейшем, при расчетах конкретных течений полидисперсной среды, будет использоваться формула (19) при малых числах М в относительном движении газ – частица или формула (20) при М³0.2. Приведем в заключение этого пункта некоторые соображения, связанные с учетом вращения частиц. При малых числах Re захват среды при вращении частицы увеличивает скорость потока на одной стороне тела и уменьшает на другой. Возникает эффект Магнуса, т.е. сила, направленная в сторону большей скорости обтекания. Однако, при отрыве потока точки отрыва будут перемещаться по поверхности сферы, вызывая силу противоположную силе Магнуса. Результаты ряда экспериментальных и теоретических работ [83] показывают, что вращение частицы не изменяет существенно коэффициента сопротивления. Можно показать, что во многих случаях остальные силы, действующие на частицу, малы по сравнению с Архимедова сила мала, т.к. мало Пример:
Силы взаимодействия между частицами также малы, если частиц в потоке мало; можно пренебречь также силой термофореза, которая возникает в потоке с неравномерной температурой газовой среды. Эта сила мала по сравнению с
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.174 (0.011 с.) |

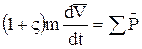 ,
, 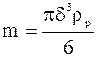 (17)
(17) - коэффициент присоединенной массы, m - масса твердой частицы,
- коэффициент присоединенной массы, m - масса твердой частицы, 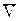 - вектор абсолютной скорости частицы,
- вектор абсолютной скорости частицы,  - сумма векторов сил, действующих на частицу,
- сумма векторов сил, действующих на частицу, 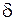 - линейный размер частицы,
- линейный размер частицы, 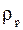 - ее плотность.
- ее плотность.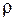 (m /
(m / 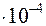 , например для частиц кварца, поэтому величиной
, например для частиц кварца, поэтому величиной 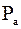 +
+ 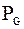 +
+ 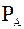 +
+ 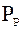
 - сила аэродинамического сопротивления;
- сила аэродинамического сопротивления;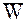 - ее движения относительно газа, и может быть записана в виде
- ее движения относительно газа, и может быть записана в виде (18)
(18)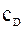 - коэффициент сопротивления,
- коэффициент сопротивления, 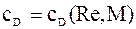 ,
, 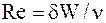 ,
,  ,
, 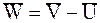 .
.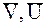 - абсолютные скорости частицы и газа.
- абсолютные скорости частицы и газа.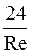 (1*)
(1*)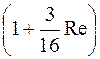
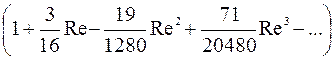 (2*)
(2*)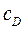 в виде
в виде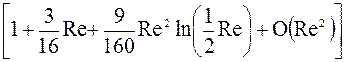 (3*)
(3*) ).
). до 4
до 4  ~1…5
~1…5  , (19)
, (19)

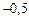
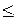 0.6
0.6
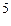
 и М=0.2 – 0.98, предложили аппроксимацию для коэффициента сопротивления в виде
и М=0.2 – 0.98, предложили аппроксимацию для коэффициента сопротивления в виде (20)
(20)
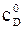 - одна из аппроксимаций стандартной кривой
- одна из аппроксимаций стандартной кривой  , сила тяжести мала, т.к. малы массы частиц.
, сила тяжести мала, т.к. малы массы частиц.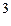 ,
, 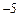 м, W=1м/c,
м, W=1м/c, 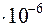 м
м  /c, то
/c, то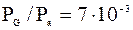 ,
, 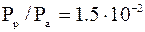 при gradP = 50Па/мм.
при gradP = 50Па/мм.


