
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем уравнений, усредненных по Рейнольдсу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистический подход к исследованию турбулентности - осреднение уравнений движения по ансамблю состояний. Все параметры движения разлагаются на среднюю и турбулентную составляющие. Рассмотрим уравнения Навье-Стокса для несжимаемой вязкой среды.
Входящие в них величины представляются в виде сумм средних полей и пульсаций.
Подставив разложения и проведя осреднение, получим уравнения Рейнольдса
где Предположение: турбулентность образуется лишь в результате перехода части энергии осредненного течения в энергию мелкомасштабных возмущений. В этом случае все статистические характеристики турбулентности (в частности, напряжения Рейнольдса) должны зависеть от поля средней скорости.
где Предположение: турбулентная вязкость и энергия турбулентных пульсаций для данного течения есть величины постоянные.
Существует достаточно большое количество моделей, дополняющих систему уравнений Рейнольдса необходимыми уравнениями с тензором напряжений Рейнольдса. В настоящей работе используется двухпараметрическая модель.
Методы исследования течения среды в ступени насоса: · Исходные уравнения, представляющие собой усреднённые по Рейнольдсу уравнения Навье-Стокса, записываются в дивергентной форме для цилиндрической системы координат (х, r, φ), вращающейся с угловой скоростью ротора Ω. · Среда предполагается однофазной сжимаемой вязкой, подчиняющейся двухпараметрическому уравнению состояния. · Течение – турбулентное. · При расчетах течения в не вращающихся областях проточной части насоса (элементов статоров, направляющих устройств и др.) удобно использовать абсолютную цилиндрическую систему координат, а для вращающихся областей проточной части (элементов ротора)–относительную систему координат, вращающуюся с соответствующей угловой скоростью ротора.
Уравнения Навье-Стокса в трехмерной нестационарной постановке: В безразмерном виде система уравнений во вращающейся цилиндрической системе координат имеет вид:
t – время, ρ – плотность, p – давление, T – температура, S – энтропия, е* – внутренняя энергия,
Модель турбулентности В безразмерном виде система уравнений во вращающейся цилиндрической системе координат имеет вид:
где
Здесь dn расстояние вдоль нормали до стенки. Значения констант, входящих в последние формулы, следующие:
Начальные условия: Начальными условиями задачи являются заданные в момент времени t=0 приближенные распределения гидродинамических параметров по всему рабочему пространству ступени насоса. Эти распределения могут вычисляться либо из решения одномерной задачи для моделируемого режима работы насоса, либо задаваться простейшим образом (например, полное отсутствие движения флюида в ступени в момент запуска насоса). Необходимым условием решения задачи является задание полной 3D геометрии всей проточной части.
Граничные условия: Граничные условия задачи: · на неподвижных стенках все компоненты скорости задаются равными нулю – условие прилипания, · на подвижных стенках скорость · на входе в насос задаются полные параметры набегающего потока, а также направление скорости; · на выходе - статическое давление окружающей среды. Другой вариант задания граничного условия на входе состоит в задании расхода флюида вместо полного давления. Такой подход дает более устойчивое решение, поэтому при проведении расчетов для надежности получаемых результатов моделировались параллельно два решения (на разных ПК) и проводилось их сравнение.
Исходные данные: Численный эксперимент проводился для ступени электроцентробежной погружной насосной установки для нефтедобычи - ЭЦН АКМ. Параметры расчета: · Рабочее тело – вода: плотность ρ = 997 кг/м3, вязкость m = 0.001003 кг/м×с, температура Т = 300 К. · Рассматривается изотермический процесс. · Частота вращения ротора насоса: ω = 10000 об/мин. В результате расчетов обнаружены существенные различия в характере течения при малых и больших расходах через ступень. В связи с этим анализ результатов будет приведен для двух предельных значений расходов, при которых проводился численный эксперимент: 30 м3/сут и 160 м3/сут.
Интегральные характеристики:
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 413; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.224 (0.009 с.) |







 - тензор напряжений Рейнольдса.
- тензор напряжений Рейнольдса. - зависимость Буссинеска
- зависимость Буссинеска - коэффициент турбулентной вязкости
- коэффициент турбулентной вязкости




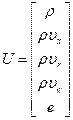














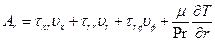





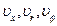 - –компоненты относительной скорости вдоль осей х, r и φ
- –компоненты относительной скорости вдоль осей х, r и φ – коэффициенты молекулярной и турбулентной вязкости,
– коэффициенты молекулярной и турбулентной вязкости, 
 и
и  - числа Прандтля; Re - число Рейнольдса
- числа Прандтля; Re - число Рейнольдса
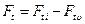



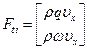



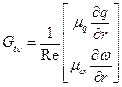

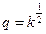

 - кинетическая энергия пульсаций
- кинетическая энергия пульсаций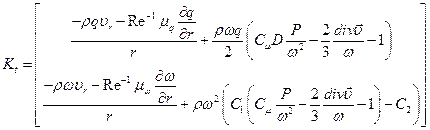
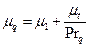
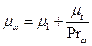
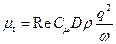
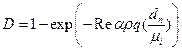
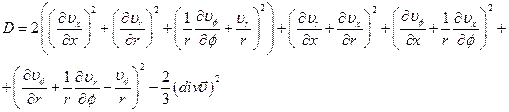
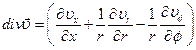
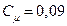
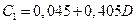
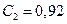
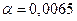


 = Ω, остальные компоненты скорости равны нулю;
= Ω, остальные компоненты скорости равны нулю;


