
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Течение в диффузоре. Назначение диффузоров. Постановка задачи о течении в диффузоре и методы решения .Содержание книги
Поиск на нашем сайте
Диффузор в гидроаэромеханике - участок проточного канала (трубопровода), в котором происходит торможение потока жидкости или газа. Поперечное сечение диффузора может быть круглым, прямоугольным, кольцевым, эллиптическим, а также несимметричным. По назначению и геометрической форме диффузор - устройство, обратное соплу. Вследствие падения средней скорости v давление р в направлении течения растёт и кинетическая энергия потока частично преобразуется в потенциальную. В отличие от сопла, преобразование энергии в диффузоре сопровождается заметным возрастанием энтропии и уменьшением полного давления. Разность полных давлений на входе и выходе диффузора характеризует его гидравлическое сопротивление и называется потерями. Потерянная часть кинетической энергии потока затрачивается на образование и затухание вихрей, совершает работу против сил трения и необратимо переходит в теплоту.
Вязкость оказывает решающее влияние на течение в диффузоре. В пограничном слое скорость под действием вязкости быстро убывает, обращаясь в нуль на стенке диффузора. Кинетическая энергия в пограничном слое меньше, чем в остальной части потока, а статическое давление в данном поперечном сечении почти постоянно. Tак как средняя скорость по длине диффузора падает, а давление растёт, то в сечении, расположенном на некотором расстоянии от входа в диффузор, кинетическая энергия потока вблизи стенки недостаточна для того, чтобы переместить жидкость или газ против сил давления, возрастающих в направлении потока. Вблизи этого сечения начинается отрыв потока от стенки и возникает возвратное течение. В результате вблизи стенки диффузора образуются области циркуляционного движения (рис. 1). Поверхность раздела между оторвавшимся от стенки и основным потоками неустойчива, она периодически свёртывается в вихри, которые сносятся вниз по потоку. Место расположения отрыва в диффузоре зависит от толщины пограничного слоя, от величины положительного градиента давления, определяемого геометрической формой диффузора, от профиля скорости и уровня турбулентности перед входом в диффузор. Чтобы рассчитать газодинамические функции для дозвукового диффузора, необходимо задать во входном сечении при x=0 полное давление P0=101000 Па и рассматриваем различные числа Маха М0=0,3; 0,5; 0,7.
Из формулы (1) определим константу, зная число Маха на входе и площадь сечения диффузора y(x). Будем считать, что через канал движется воздух, тогда γ=1,4. Теперь мы знаем константу и можем определить распределение числа Маха в диффузоре на интервале от x=0 до x=1 по формуле (1).
Определим распределение скорости газа в диффузоре. Так как мы знаем распределение числа Маха, то мы можем найти и распределение скорости по формуле: Распределение давления газа в диффузоре определим с помощью формулы 2.
Чтобы найти точку отрыва газа от стенок диффузора, воспользуемся следующими формулами:
Чтобы посчитать Чтобы рассчитать по формуле (3) Для турбулентного пограничного слоя в несжимаемой жидкости (М=0) с характерным размером Постановка задачи 1. Задаём p0, M0 (во входном сечении); 2. Задаёмгеометрию диффузора; 3. По заданному М0 и р0 определяем константу на входе, по полученной константе определяем распределение числа Маха в диффузоре; 4. Определяем распределение скорости в диффузоре; 5. Аппроксимируем все данные, превращая их в функции одной переменной; 6. Находим производную давления по х; 7. Решаем уравнение для Z.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.166 (0.008 с.) |



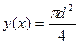 .
. , где
, где  - это скорость звука (
- это скорость звука ( м/с).
м/с).

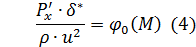
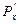 , дискретную зависимость давления от длины диффузора P(x) надо интерполлировать, т.е. провести через все точки непрерывную кривую, зависящую от x. Для этой цели воспользуемся встроенной процедурой в Maple.
, дискретную зависимость давления от длины диффузора P(x) надо интерполлировать, т.е. провести через все точки непрерывную кривую, зависящую от x. Для этой цели воспользуемся встроенной процедурой в Maple. - толщину вытеснения, нам нужны входящие в него величины. Плотность воздуха
- толщину вытеснения, нам нужны входящие в него величины. Плотность воздуха  кг/м3, константы А=0,017 и С=5,7 для толщины вытеснения,
кг/м3, константы А=0,017 и С=5,7 для толщины вытеснения,  Па·с – вязкость воздуха. Зададим начальную толщину вытеснения
Па·с – вязкость воздуха. Зададим начальную толщину вытеснения  и рассчитаем распределение
и рассчитаем распределение  .
.
 . Это значение вычислено на основании экспериментальных работ. Рассчитаем зависимость
. Это значение вычислено на основании экспериментальных работ. Рассчитаем зависимость  по формуле (4) (мы знаем все входящие в него величины).
по формуле (4) (мы знаем все входящие в него величины).


