
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характерные скорости движения молекул газаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Среднеквадратичная скорость
Подставляя
Характерные скорости движения молекул газа Хотя Уравнение дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость. Наиболее вероятная скорость наиболее вероятная скорость,
Средняя скорость
Подставляя
Среднеквадратичная скорость
Подставляя
Статисти́ческая механика (статистическая физика) — раздел теоретической физики, в котором изучаются свойства и поведение систем (макроскопических физических тел), состоящих из очень большого числа частиц (атомов, молекул, заряженных частиц — ионов, электронов или квантов излучения — фотонов) Исследование свойств и поведения физических тел, состоящих из колоссального числа частиц, позволили выявить их важную принципиальную особенность. Она заключается в том, что их поведение определяется закономерностями особого типа, получившими название статистических закономерностей. Статистические методы дают возможность вычислять средние значения величин, характеризующих свойства макроскопических тел (такие, например, как плотность, давление, температура и т.п.). Проявление статистических закономерностей заключается в том, что поведение этих средних величин никак не зависит от конкретных начальных условий, характеризующих движение отдельных частиц, входящих в состав данного тела (т.е. от точных значений начальных координат и скоростей частиц). Другими словами, макроскопическое состояние системы как бы «забывает» о прошлом, тогда как при чисто механическом описании движения микроскопических частиц будущее системы однозначно определяется прошлым.
Согласно молекулярно-кинетической теории газов движение молекул носит беспорядочный характер; эта беспорядочность относится ко всем видам движения молекулы. Ни один из видов движения не имеет преимущества перед другим. При статистическом равновесии движений энергия в среднем распределяется равномерно между всеми видами движения. Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной
ТЕПЛОТА И ТЕМПЕРАТУРА тела при разной температуре могут обладать одинаковой тепловой энергией, и наоборот: тела с одинаковой температурой могут иметь разную тепловую энергию. Энтальпия — количество тепла, содержащегося в единице массы вещества. Эта величина измеряется в кДж/кг
Распределение Больцмана
Где dwx,y,z - число молекул, у которых координата х лежит в пределах от х до х + dx, при этом y лежит в пределах от y до y + dy и координата z в пределах от z до z + dz; U(x,y,z) - потенциальная энергия молекулы во внешнем силовом поле. Из формулы выше следует, что
где n(x, y, z) - концентрация молекул в в физически малом объеме вблизи точки (x, y, z). Полагая n(x0, y0, z0) = n0, где n0 - концентрация газа там, где U(x0, y0, z0) = 0, получаем распределение Больцмана в общем виде
В качестве примера рассмотрим распределение газа в атмосфере Земли (считая температуру постоянной). Для молекулы газа вблизи поверхности Земли
, где z - высота над поверхностью Земли. Тогда концентрация молекул на высоте z:
где n0 - концентрация молекул у поверхности Земли. Используя уравнение состояния идеального газа P = nkT, получим зависимость атмосферного давления от высоты
Концентрация молекул газа тем выше, чем меньше их потенциальная энергия. А при стремлении температуры к абсолютному нулю, молекулы начинают скапливаться в месте, где их потенциальная энергия принимает наименьшее значение. Указанные особенности распределения Больцмана являются следствием теплового движения молекул, так как кинетическая энергия их поступательного движения в среднем равна
Распределение Больцмана при дискретных уровнях энергии. Полученное Больцманом распределение относится к случаям, когда молекулы находятся во внешнем поле и их потенциальная энергия распределение Больцмана имеет вид:
где
где N – полное число частиц в рассматриваемой системе. Тогда
5 Явления переноса в газах. Молекулы в газе движутся со скоростью звука. Однако, находясь в противоположном конце комнаты, запах разлитой пахучей жидкости мы почувствуем через сравнительно большой промежуток времени. Это происходит потому, что молекулы движутся хаотически, сталкиваются друг с другом, траектория движения у них ломанная. Явления, происходящие в газах: · В состоянии равновесия температура Т и концентрация n во всех точках системы одинакова. При отклонении плотности от равновесного значения в некоторой части системы возникает движение компонент вещества в направлениях, приводящих к выравниванию концентрации по всему объему системы. Связанный с этим движением перенос вещества обусловлен диффузией. Диффузионный поток будет пропорционален градиенту концентрации: · Если какое-либо тело движется в газе, то оно сталкивается с молекулами газа и сообщает им импульс. С другой стороны, тело тоже будет испытывать соударения со стороны молекул, и получать собственный импульс, но направленный в противоположную сторону. Газ ускоряется, тело тормозится, то есть на тело действуют силы трения. Такая же сила трения будет действовать и между двумя соседними слоями газа, движущимися с разными скоростями. Это явление носит название внутреннее трение или вязкость газа, причём сила трения пропорциональна градиенту скорости:
· Если в соседних слоях газа создана и поддерживается разность температур, то между ними будет происходить обмен тепла. Благодаря хаотическому движению, молекулы в соседних слоях будут перемешиваться и их средние энергии будут выравниваться. Происходит перенос энергии от более нагретых слоев к более холодным телам. Этот процесс называется теплопроводностью. Поток тепла пропорционален градиенту температуры:
· В состоянии равновесия в среде, содержащей заряженные частицы, потенциал электрического поля в каждой точке соответствует минимуму энергии системы. При наложении внешнего электрического поля возникает неравновесное движение электрических зарядов в таком направлении, чтобы минимизировать энергию системы в новых условиях. Связанный с этим движением перенос электрического заряда называется электропроводностью, а само направленное движение зарядов - электрическим током. В процессе диффузии при теплопроводности и электропроводности происходит перенос вещества, а при внутреннем трении – перенос энергии. В основе этих явлений лежит один и тот же механизм – хаотическое движение молекул. Длина свободного пробега молекулы — это среднее расстояние (обозначаемое Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега (<λ>). Величина <λ> является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры.
Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение. Сила вязкого трения F пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h:
Различают динамическую вязкость (единицы измерения: Па·с = 10 Пуаз) и кинематическую вязкость (единицы измерения: Стокс, м²/с, внесистемная единица — градус Энглера) Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества. ВЯЗКОСТЬ ГАЗОВ В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле
где Вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа ВЯЗКОСТЬ ЖИДКОСТЕЙ Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Справедлив общий закон внутреннего трения — закон Ньютона:
Коэффициент вязкости -
Коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества
где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского. Динамическая вязкость жидкостей уменьшается с увеличением температуры, и растёт с увеличением давления.
В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной
и эта величина получила название кинематической вязкости. Здесь
Пусть имеются две параллельные пластинки, между которыми находится газ (жидкость). Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0. Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е.
Постоянная a определяется из условия, что при x = h u = u0, т. е. u0 = ah. Откуда a = u0/h. Тогда выражение (3.3.1) примет вид
Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения. Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е.
где
Так как из (3.3.2) следует, что
Закон утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения. Физический смысл коэффициента вязкости Согласно второму закону Ньютона,
Таким образом, с точки зрения молекулярно-кинетической теории в процесс внутреннего трения каждая молекула переносит упорядоченный импульс
7. Теплопрово́дность — это процесс переноса внутренней энергии от более нагретых частей тела (или тел) к менее нагретым частям (или телам), осуществляемый хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. (количественная характеристика способности конкретного вещества проводить тепло) В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
где Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры).
В интегральной форме это же выражение запишется так
где Коэффициент теплопроводности измеряется в Вт/(м·K).
Коэффициент теплопроводности газов определяется формулой:
Где: i — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5, для одноатомного i=3), k — постоянная Больцмана, M — молярная масса, T — абсолютная температура, d — эффективный диаметр молекул, R — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные. ВЫВОД ФОРМУЛ: Для количественного описания термодинамического потока вводят величину В общем случае поток
где:
Если рассматриваемая термодинамическая система находится в состоянии, близком к равновесию, то плотность термодинамического потока
где Из выражения (6.3) следует, что плотность термодинамического потока Величина В случае если величина
или для потока
8. Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики. Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Законы поведения огромного числа молекул, являясь статистическими закономерностями, изучаются с помощью статистического метода. Этот метод основан на том, что свойства макроскопической системы в конечном счете определяются свойствами частиц системы, особенностями их движения и усредненными значениями динамических характеристик этих частиц (скорости, энергии и т. д.). Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул. Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных. Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества.
Равнове́сный тепловой процесс — тепловой процесс, в котором система проходит непрерывный ряд бесконечно близких равновесных термодинамических состояний. Равновесный тепловой процесс называется обратимым, если его можно провести обратно и в телах, окружающих систему, не останется никаких изменений. Реальные процессы изменения состояния системы всегда происходят с конечной скоростью, поэтому не могут быть равновесными. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается, поэтому равновесные процессы называют квазистатическими. Уравнение идеального газа в отношении его давления записывается обычно в виде
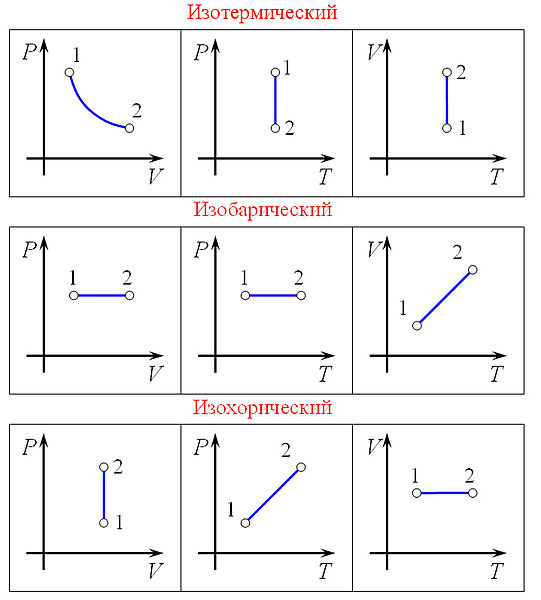
В этом выражении Rg - универсальная газовая постоянная, а T - температура и r- плотность. Изотермический процесс процесс изменения состояния термодинамической системы при постоянной температуре ( При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const. Изохорный процесс процесс изменения состояния термодинамической системы при постоянном объёме (
Ещё стоит указать что поданная к газу энергия расходуется на изменение внутренней энергии то есть Q = 3* ν*R*T/2=3*V*ΔP, где R — универсальная газовая постоянная, ν количество молей в газе, T температура в Кельвинах, V объём газа, ΔP приращение изменения давления, а линию, изображающая изохорный процесс на диаграмме, в осях Р(Т), стоит продлить и пунктиром соединить с началом координат, так как может возникнуть недопонимание. Изобарный процесс процесс изменения состояния термодинамической системы при постоянном давлении (
Закон Гей-Люссака: При постоянном давлении и неизменных значениях массы газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
Параметры состояния Вещества обычно пребывают в одном из трех основных состояний: в виде газа, жидкости или твердого тела. Очевидно, что одно и то же тело, одно и то же вещество при разных условиях может находиться в различных состояниях. В заданных неизменных условиях рассматриваемое вещество всегда будет находиться в одном и том же состоянии, например при атмосферном давлении и температуре 400 °С вода будет существовать только в виде пара, но никак не в виде жидкости или твердого вещества. Свойства вещества могут быть интенсивными и экстенсивными. Интенсивными называют свойства, не зависящие от количества вещества в системе (давление, температура и некоторые другие). Примером экстенсивных свойств является объем, который изменяется в данных условиях пропорционально количеству вещества: объем 10 кг вещества будет в 10 раз больше, чем объем 1 кг. Удельные, т. е. отнесенные к массе вещества, экстенсивные свойства приобретают смысл интенсивных свойств. Так, удельный объем, удельная теплоемкость и т. п. могут рассматриваться как интенсивные свойства. Интенсивные свойства, определяющие состояние тела или группы тел — термодинамической системы — называют термодинамическими параметрами состояния тела (системы). Наиболее удобными и поэтому наиболее распространенными параметрами состояния являются абсолютная температура, абсолютное давление и удельный объем (или плотность) тела. Одним из важнейших параметров является абсолютная температура. Температура характеризует тепловое состояние тела. Как хорошо известно из опыта, теплота может самопроизвольно переходить лишь от более нагретых тел к менее нагретым, т. е. от тел с большей температурой к телам с меньшей температурой. Таким образом, температуры тел определяют направление возможного самопроизвольного перехода теплоты между этими телами.
Закон возрастания энтропии Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 3.13.
Пусть процесс
Так как процесс
Подстановка этой формулы в неравенство (3.55) позволяет получить выражение
Сравнение выражений (3.53) и (3.57) позволяет записать следующее неравенство
в котором знак равенства имеет место в случае, если процесс Неравенство (3.58) может быть также записано и в дифференциальной форме
Если рассмотреть адиабатически изолированную термодинамическую систему, для которой
или в интегральной форме
Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом: Принцип возрастания энтропии сводится к утверждению, что энтропия изолированных систем неизменно возрастает при всяком изменении их состояния и остается постоянной лишь при обратимом течении процессов Записанное утверждение является ещё одной формулировкой второго начала термодинамики. Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия. Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. 13. а) Тепловой двигатель. Периодический тепловой двигатель. Рабочее тело. б) Используя графический метод, показать, что для работы периодического теплового двигателя незамкнутого процесса недостаточно. в) Какой процесс называют обратимым? Что такое нагреватель, холодильник? Какова их роль в работе теплового двигателя? г) Начертите и объясните схему превращения в тепловых двигателях внутренней энергии топлива в механическую работу. д) Как формулируют второе начало термодинамики? В чем состоит физический смысл этого закона? Цикл Карно Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.
При первом изотермическом процессе 1-2 происходит передача рабочему телу теплоты
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 3851; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.013 с.) |

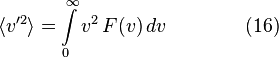
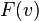 и интегрируя, мы получим
и интегрируя, мы получим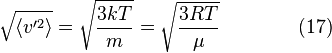
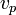 — вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению
— вероятность обладания которой любой молекулой системы максимальна, и которая соответствует максимальному значению 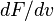 , приравнять её нулю и решить относительно
, приравнять её нулю и решить относительно 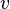 :
: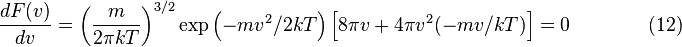
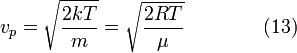
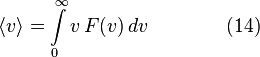
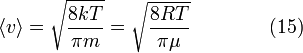
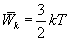 . Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия
. Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия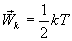
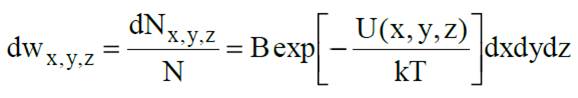 Как показал Больцман, при наличии внешнего потенциального поля вероятность dwx,y,z того, что молекула (взятая наугад) окажется в элементе объема dV = dxdydz вблизи точки с координатами x, y, z
Как показал Больцман, при наличии внешнего потенциального поля вероятность dwx,y,z того, что молекула (взятая наугад) окажется в элементе объема dV = dxdydz вблизи точки с координатами x, y, z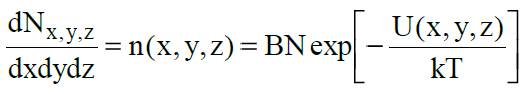
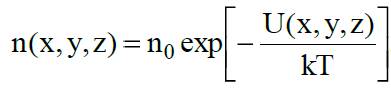
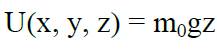
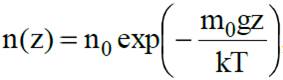
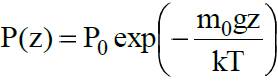 которая называется барометрической формулой.
которая называется барометрической формулой.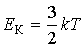 и уменьшается пропорционально уменьшению температуры. А уменьшение кинетической энергии приводит к уменьшению количества молекул, способных преодолеть потенциальный порог, высота которого характеризуется величиной потенциальной энергии высотой
и уменьшается пропорционально уменьшению температуры. А уменьшение кинетической энергии приводит к уменьшению количества молекул, способных преодолеть потенциальный порог, высота которого характеризуется величиной потенциальной энергии высотой 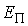 .
.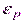 может применяться непрерывно. Больцман обобщил полученный им закон на случай распределения, зависящего от внутренней энергии молекулы.
может применяться непрерывно. Больцман обобщил полученный им закон на случай распределения, зависящего от внутренней энергии молекулы.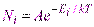 ,
,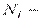 число частиц в состоянии с энергией
число частиц в состоянии с энергией 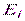 ;
;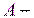 коэффициент пропорциональности, который удовлетворяет условию
коэффициент пропорциональности, который удовлетворяет условию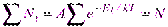 ,
,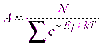 и в результате для случая дискретных значений энергии распределение Больцмана:
и в результате для случая дискретных значений энергии распределение Больцмана: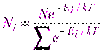
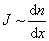
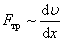 .
.
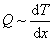 .
.
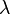 ), которое частица пролетает за время свободного пробега от одного столкновения до следующего.
), которое частица пролетает за время свободного пробега от одного столкновения до следующего.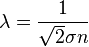
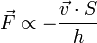
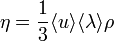 ,
,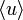 — средняя скорость теплового движения молекул,
— средняя скорость теплового движения молекул, 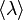 − средняя длина свободного пробега,
− средняя длина свободного пробега, 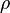 - плотность.
- плотность.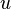 , растущей с температурой как
, растущей с температурой как 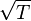
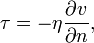
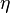
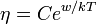
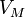 . Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение
. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение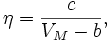
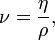
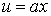 (3.3.1)
(3.3.1)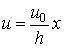 (3.3.2)
(3.3.2)
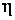 – постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения
– постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения 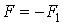 , равенство (3.3.3) перепишем в виде
, равенство (3.3.3) перепишем в виде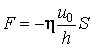
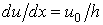 , то последнее выражение можно представить так:
, то последнее выражение можно представить так: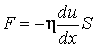
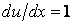
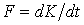 , где K – импульс элементарной массы слоя газа. Поэтому формулу выше можно представить в виде бесконечно малых:
, где K – импульс элементарной массы слоя газа. Поэтому формулу выше можно представить в виде бесконечно малых:
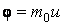 , вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса
, вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса 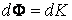 , получим:
, получим: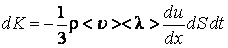
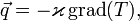
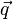 — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси,
— вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, 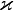 — коэффициент теплопроводности (иногда называемый просто теплопроводностью),
— коэффициент теплопроводности (иногда называемый просто теплопроводностью), 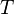 — температура.
— температура.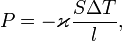
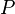 — полная мощность тепловых потерь,
— полная мощность тепловых потерь, 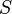 — площадь сечения параллелепипеда,
— площадь сечения параллелепипеда, 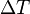 — перепад температур граней,
— перепад температур граней, 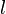 — длина параллелепипеда, то есть расстояние между гранями.
— длина параллелепипеда, то есть расстояние между гранями.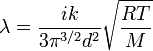
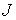 , численно равную количеству физической величины, переносимой за одну секунду через выбранную поверхность. В случае диффузии поток
, численно равную количеству физической величины, переносимой за одну секунду через выбранную поверхность. В случае диффузии поток 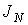 определяет интенсивность переноса частиц примеси; при теплопроводности величина
определяет интенсивность переноса частиц примеси; при теплопроводности величина 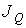 численно равна количеству теплоты, переносимой за единицу времени; для явления вязкости величина
численно равна количеству теплоты, переносимой за единицу времени; для явления вязкости величина 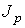 характеризует перенос импульса.
характеризует перенос импульса.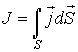
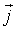 - плотность термодинамического потока,
- плотность термодинамического потока, 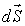 - вектор, численно равный величине элементарной поверхности
- вектор, численно равный величине элементарной поверхности 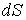 и направленный по нормали к этой поверхности. Если термодинамический поток однороден и вектор
и направленный по нормали к этой поверхности. Если термодинамический поток однороден и вектор 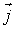 во всех точках среды одинаков и перпендикулярен поверхности, то величина потока
во всех точках среды одинаков и перпендикулярен поверхности, то величина потока 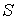 , определяется по формуле:
, определяется по формуле: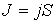 где
где 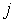 - абсолютное значение (модуль) вектора
- абсолютное значение (модуль) вектора 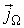 пропорциональна градиенту соответствующей физической величины
пропорциональна градиенту соответствующей физической величины 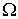 в той же точке:
в той же точке: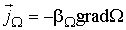 (6.3)
(6.3)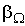 - коэффициенты переноса, или кинетические коэффициенты.
- коэффициенты переноса, или кинетические коэффициенты.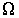 от точки к точке пространства. Кроме этого, знак минус в этом выражении указывает на то, что поток
от точки к точке пространства. Кроме этого, знак минус в этом выражении указывает на то, что поток 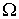 зависит от описываемого процесса. При описании диффузии в качестве параметра
зависит от описываемого процесса. При описании диффузии в качестве параметра 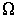 выступает относительная концентрация примеси, а коэффициент переноса
выступает относительная концентрация примеси, а коэффициент переноса 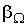 представляет собой коэффициент диффузии
представляет собой коэффициент диффузии 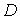 . Для случая теплопроводности вместо
. Для случая теплопроводности вместо 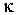 . Параметром
. Параметром 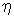 .
.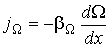
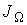 :
: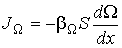
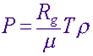
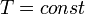 )(
)(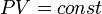 ). Изотермический процесс описывается законом Бойля — Мариотта:
). Изотермический процесс описывается законом Бойля — Мариотта: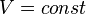 ).Закон Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:
).Закон Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре: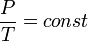
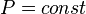 )
)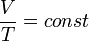

 будет необратимым, а процесс
будет необратимым, а процесс  - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид
- обратимым. Тогда неравенство Клаузиуса для этого случая примет вид .
.
 .
.
 .
.
 ,
,
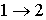 является обратимым, а знак больше, если процесс
является обратимым, а знак больше, если процесс  - необратимый.
- необратимый. .
.
 , то выражение (3.59) примет вид
, то выражение (3.59) примет вид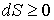
 .
.
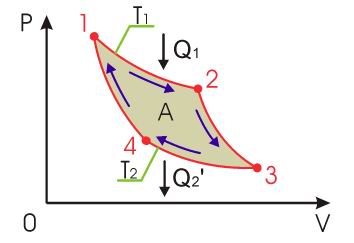
 , причем эта теплота передается бесконечно медленно, при практически нулевой разнице температуры между на
, причем эта теплота передается бесконечно медленно, при практически нулевой разнице температуры между на 


