
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение молекулярно-Кинетической теории газа (уравнение Клаузиуса 1857г.)Содержание книги
Поиск на нашем сайте
Выделим на стенке сосуда произвольную элементарную площадку ΔS (рис.1) и подсчитаем число соударений с ней за время Δt. Очевидно, оно равно числу молекул, которые за это время успеют долететь до элемента поверхности ΔS.Eсли внешние условия постоянны, то сумма кинетических энергий молекул газа тоже будет постоянной. Так что убывание скорости одной молекулы приводит к возрастанию скорости другой и наоборот. Принимая во внимание огромное число таких процессов можно считать, что распределение молекул по значениям скоростей неизменно, т.е. число молекул, которые движутся с той или иной скоростью не меняется. Применим эти рассуждения к прямому цилиндру (рис.1), построенному на элементе ΔS как основании. Направим одну из осей координат (X, Y или Z) вдоль нормали к ΔS. Получим, что число частиц ΔNi, имеющих скорость ui и достигших элемента стены ΔS за время Δt:
где ni - число молекул i-ого сорта в единице объема, т.е. таких, которые имеют скорость ui; ∆Ѕ∙υi∙∆t - объем цилиндра, содержащего молекулы i-ого сорта, способные долететь до элемента ∆Ѕ за время ∆t. При соударении каждая такая молекула массой m изменяет свой импульс на величину: |∆(mυi)| = |- mυi- mυi| = 2 mυi (2). Тогда элемент поверхности получает при единичном соударении импульс силы fi∙∆t = 2mυi, а суммарный импульс, переданный всеми молекулами i-ого сорта элементу ∆Ѕ за время ∆t: fi∙∆t = ∆Ni ∙2mυi = где
p = Это и есть основное уравнение МКТ: давление идеального газа равно 2/3 кинетической энергии поступательного движения частиц в единице объема.
1. Средняя квадратическая скорость и средняя кинетическая энергия движения молекул идеального газа. Степени свободы. Распределение энергии по степеням свободы. Внутренняя энергия идеального газа. МКТ. Введем для этого понятие о средней кинетической энергии молекулы идеального газа как p = Получим выражение для сред. кинетической энергии молекулы:
Найдем взаимосвязь pVμ = Здесь nVμ = NА - число Авагадро. Сопоставляя (11) с уравнением состояния (уравнение Менделеева-Клапейрона) для моля идеального газа – pVμ = RT, имеем RT =
Здесь, Формула (12) позволяет сделать очень важный вывод: абсолютная температура идеального газа прямо пропорциональна средней энергии поступательного движения частиц. В молекулярной физике под внутренней энергией идеального газа понимают сумму кинетических энергий всех молекул (молекулярное взаимодействие отсутствует).
Тогда кинетическая энергия каждой отдельной молекулы будет определяться формулой:
где j – число степеней свободы молекулы. Таким образом, проблема внутренней энергии газа сводится к определению числа степеней свободы, которое следует приписать его молекулам. одноатомные газы имеют только три степени свободы поступательного движения (рис.4а). Двухатомной молекуле с жесткой связью между атомами следует приписать пять степеней свободы: три поступательного и две вращательного. Для молекул с числом атомов три и более (рис.4в), которые связаны между собой жестко, число степеней свободы равно шести. Внутренняя энергия одного моля идеального газа:
где j = 3 для одноатомных; j = 5 для двухатомных; j = 6 для трёхатомных молекул. Для произвольной массы газа m:
1.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.224 (0.005 с.) |

 Воспользуемся моделью идеального газа: размеры его молекул столь малы, что их суммарным объемом можно пренебречь по сравнению с объемом сосуда; подавляющую часть времени каждая молекула движется свободно и лишь иногда испытывает упругие столкновения с другими молекулами и стенками сосуда. При ударе о стенку молекула передает ей некоторый импульс силы – FmΔtm, численно равный изменению количества движения молекулы – Δ(mυ). Каждый элемент поверхности стенки ΔS непрерывно подвергается "бомбардировке" большим количеством молекул, что и создает силовое воздействие, т.е. давление, со стороны молекул на стенку, которое направлено по нормали к ней.
Воспользуемся моделью идеального газа: размеры его молекул столь малы, что их суммарным объемом можно пренебречь по сравнению с объемом сосуда; подавляющую часть времени каждая молекула движется свободно и лишь иногда испытывает упругие столкновения с другими молекулами и стенками сосуда. При ударе о стенку молекула передает ей некоторый импульс силы – FmΔtm, численно равный изменению количества движения молекулы – Δ(mυ). Каждый элемент поверхности стенки ΔS непрерывно подвергается "бомбардировке" большим количеством молекул, что и создает силовое воздействие, т.е. давление, со стороны молекул на стенку, которое направлено по нормали к ней. , (1)
, (1) ∙2mυi =
∙2mυi =  (3).
(3). – кинетическая энергия поступательного движения одной частицы, движущейся со скоростью υi.
– кинетическая энергия поступательного движения одной частицы, движущейся со скоростью υi. (6).
(6). = w представляет собой суммарную кинетическую энергию всех молекул в единице объема, т.е. объемную плотность энергии поступательного движения. Теперь (6) примет вид:
= w представляет собой суммарную кинетическую энергию всех молекул в единице объема, т.е. объемную плотность энергии поступательного движения. Теперь (6) примет вид: w
w 
 . Тогда w
. Тогда w  и примет вид:
и примет вид: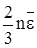 . (8)
. (8) . (9)
. (9) с макропараметрами идеального газа (давлением – р, объёмом – V и температурой – T). Умножим (8) на молярный объем Vμ:
с макропараметрами идеального газа (давлением – р, объёмом – V и температурой – T). Умножим (8) на молярный объем Vμ: . (11)
. (11) , что дает:
, что дает: . (12)
. (12) – постоянная Больцмана, k = 1,38∙10-23 Дж/К.
– постоянная Больцмана, k = 1,38∙10-23 Дж/К. Полученное нами выражение для средней кинетической энергии молекулы
Полученное нами выражение для средней кинетической энергии молекулы  учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других виды движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота – α, β, γ. Бильярдный шар на плоскости имеет две степени свободы поступательного движения и три степени свободы вращательного движения. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение макросистемы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. На одну степень приходится:
учитывает только энергию поступательного движения. Однако наряду с поступательным движением возможно также вращение молекул и колебания атомов, входящих в их состав. Понятно, эти виды движения тоже связаны с некоторым запасом энергии. Возникает вопрос, какая доля энергии приходится на тот или другой вид движения? Чтобы ответить на него, введем понятие степени свободы. Под степенями свободы понимают те независимые от других виды движения, которые может совершать данное тело. Например, любое тело обладает тремя степенями свободы поступательного движения: вправо-влево, вперед-назад, вверх-вниз. Кроме того, тело может совершать три независимых вращательных движения вокруг трех пространственных осей. Изменение положения тела из-за вращения определяется углами поворота – α, β, γ. Бильярдный шар на плоскости имеет две степени свободы поступательного движения и три степени свободы вращательного движения. Таким образом, число степеней свободы любого тела или системы тел равно количеству независимых величин (координат), с помощью которых может быть задано положение макросистемы в пространстве. Исходя из хаотичности молекулярного движения, Максвелл и Больцман пришли к принципу равномерного распределения кинетической энергии молекул по всем степеням свободы. Это значит, что на одну степень свободы поступательного, вращательного или колебательного движения должна приходится одна и та же величина энергии. На одну степень приходится: . (16)
. (16) . (17)
. (17) , (19)
, (19)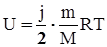 . (20)
. (20)


