
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика вращательного движения: момент силы, момент инерции тела. Теорема штейнера. Основное уравнение динамики вращательного движения.Стр 1 из 11Следующая ⇒
Динамика вращательного движения: момент силы, момент инерции тела. Теорема Штейнера. Основное уравнение динамики вращательного движения.
С учетом (16) Fi,t=Dmiri×b. (21) Умножив (21) на ri, получим:
Моментом силы называется вектор, модуль которого равен произведению модуля силы на длину плеча. Направление вектора Плечом силы называется кратчайшее расстояние от оси вращения до линии действия силы. Скалярная величина Просуммируем (23) по всем элементам массы тела:
Здесь Равенство (24) называется основным уравнением динамики вращательного движения. Т.к. скалярная величина J всегда положительная, то векторные величины Моментом импульса материальной точки относительно оси вращения называют векторную величину, модуль которой
Тогда момент импульса абсолютно твердого тела относительно неподвижной оси вращения
т.е. правление Вынужденные колебания. Явление резонанса. Начальная фаза и амплитуда при резонансе. Резонансная частота.
Свободные колебания в силу наличия трения всегда будут затухающими. Чтобы колебания были незатухающими необходимо компенсировать потери энергии. Если рассматривать механические колебания, то роль фактора восполняющего эти потери может играть внешняя переменная сила, которую называют вынуждающей. УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ Получим уравнение плоской волны в однородной среде вдоль оси 0х, совпадающей с направлением её распространения. Т.к., в этом случае фронт волны перпендикулярен 0х, то смещения s частиц среды будут зависеть только от координаты х и момента времени t, т.е. уравнение волны будет представлять собой функцию – s = f(x,t). Пред-положим, что в точке 0 (рис.1) частица совершает колебания по гармоническому закону: s = Acosωt. s = A cosω(t-τ) (1)
Если обозначить скорость волны через u, то время запаздывания, за которое волна добежит от точки 0 до точки М: τ = х/u, и уравнение колебаний в произвольной точке М на расстоянии х от источника примет вид: s= A cos ω(t-τ) = A cos ω(t - Это и есть искомое уравнение плоской бегущей волны. Здесь: А – амплитуда смещения частиц среды от положения равновесия, ω – циклическая частота колебаний частиц, ω(t - Расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе, называется длиной волны λ (рис.1). Длина волны равна расстоянию, на которое распространяется определенная фаза колебаний за период колебаний частиц среды. Тогда λ = u·T = u /ν. Т.к. ω = 2πν, то (2) можно переписать в виде: s = Acosω(t - Покажем, что скорость распространения волны u – это скорость перемещения фиксированного значения фазы. Положим ω(t – Скорость распространения механических волн зависит от физических свойств среды. Скорость распространения продольных волн определяется формулой:
Основные свойства волн: прямолинейность распространения в однородной среде, отражение и преломление на границе раздела сред, дисперсия, интерференция и дифракция. ВОЛНОВОЕ УРАВНЕНИЕ
В трехмерном случае:
УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА Из всех уравнений состояния реального газа, предложенных в свое время, самым простым и достаточно точным оказалось уравнение голландского физика Ван-дер-Ваальса:
Как видно, оно получено из уравнения Клапейрона для моля идеального газа путем введения поправок. Константы а и b имеют различные значения для разных газов и определяются опытным путем. Поправка «b» определяет ту часть объема, занимаемого газом, которая недоступна для движения из-за конечных размеров самих молекул. b = 4 Vмолекул. Поправка ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ Согласно представлениям современной физики воздействие одного заряда на другой передается через электростатическое поле – особую бесконечно простирающуюся материальную среду, которую создает вокруг себя каждое заряженное тело. Т.к. направление силы зависит от знака заряда, то условились использовать для исследования полей, так называемый, пробный заряд q0. Это положительный, точечный заряд, который помещают в интересующую нас точку электрического поля. Соответственно в качестве силовой характеристики поля целесообразно использовать отношение силы
Эта постоянная для каждой точки поля векторная величина равная силе, действующей на единичный, положительный заряд называется напряженностью. Для поля точечного заряда q на расстоянии r от него:
Направление вектора При наложении друг на друга нескольких электростатических полей, результирующая напряженность определяется как векторная сумма напряженностей каждого из полей (принцип суперпозиции):
Графически распределение электрического поля в пространстве изображается с помощью силовых линий. Эти линии проводятся так, чтобы касательные к ним в любой точке совпадали с Динамика вращательного движения: момент силы, момент инерции тела. Теорема Штейнера. Основное уравнение динамики вращательного движения.
С учетом (16) Fi,t=Dmiri×b. (21) Умножив (21) на ri, получим:
Моментом силы называется вектор, модуль которого равен произведению модуля силы на длину плеча. Направление вектора
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.43.142 (0.026 с.) |
 Установим взаимосвязь между кинематическими и динамическими параметрами вращательного движения. Пусть твердое тело вращается вокруг неподвижной оси ZZ′. Т.к. все точки тела движутся по окружностям, плоскость которых перпендикулярна оси вращения, то это означает, что равнодействующие сил приложенных к каждой точке лежат в плоскости траекторий. Разложим равнодействующую сил
Установим взаимосвязь между кинематическими и динамическими параметрами вращательного движения. Пусть твердое тело вращается вокруг неподвижной оси ZZ′. Т.к. все точки тела движутся по окружностям, плоскость которых перпендикулярна оси вращения, то это означает, что равнодействующие сил приложенных к каждой точке лежат в плоскости траекторий. Разложим равнодействующую сил  , приложенную к элементу массы D m i на две составляющие:
, приложенную к элементу массы D m i на две составляющие:  – вдоль радиуса
– вдоль радиуса 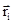 и
и  – касательную к траектории. Нормальная составляющая сил
– касательную к траектории. Нормальная составляющая сил 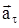 . По второму закону Ньютона
. По второму закону Ньютона . (20)
. (20)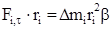 , (22)
, (22)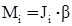 , (23)
, (23) – момент силы
– момент силы 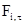 относительно оси ZZ′.
относительно оси ZZ′. перпендикулярно к плоскости, в которой лежит вектор силы, и определяется по правилу буравчика.
перпендикулярно к плоскости, в которой лежит вектор силы, и определяется по правилу буравчика. называется момент инерции материальной точки относительно осивращения ZZ′.
называется момент инерции материальной точки относительно осивращения ZZ′.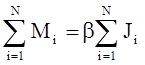 . Получим:
. Получим: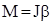 или в векторном виде
или в векторном виде  (24)
(24)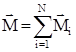 - результирующий момент силы, действующий на тело;
- результирующий момент силы, действующий на тело;  - момент инерции тела.
- момент инерции тела.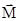 и
и 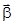 всегда направлены в одну сторону вдоль оси вращения тела.
всегда направлены в одну сторону вдоль оси вращения тела.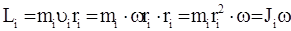 .
. 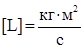 (25)
(25)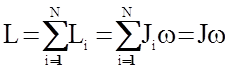 или в векторной форме
или в векторной форме 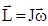 , (26)
, (26)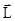 лежит на оси вращения и совпадает по направлению с
лежит на оси вращения и совпадает по направлению с  (на-
(на-
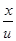 ). (2)
). (2)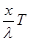 ) = Acos2π(v t -
) = Acos2π(v t - 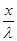 ) = Acos(ωt - 2π
) = Acos(ωt - 2π 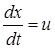 (С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью.
(С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью. . Для поперечных волн –
. Для поперечных волн –  . Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.
. Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.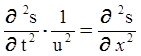 ;
; 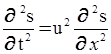 . (5)
. (5)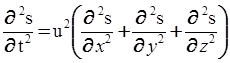
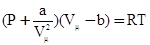

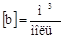
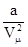 определяет внутренне давление р´, обусловленное взаимным притяжением молекул друг к другу. Очевидно, если бы вдруг это притяжение исчезло, то для того, чтобы удержать газ в пределах того же объема, пришлось бы увеличить внешнее давление на:
определяет внутренне давление р´, обусловленное взаимным притяжением молекул друг к другу. Очевидно, если бы вдруг это притяжение исчезло, то для того, чтобы удержать газ в пределах того же объема, пришлось бы увеличить внешнее давление на:  .Для произвольного количества газа
.Для произвольного количества газа  уравнение Ван-дер-Ваальса имеет вид:
уравнение Ван-дер-Ваальса имеет вид: 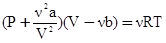 .
. к величине пробного заряда q0:
к величине пробного заряда q0: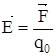 . (3)
. (3)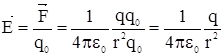 , (4)
, (4)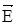 совпадает с направлением силы, действующей на пробный заряд. [E] = Н / Кл или В/м.
совпадает с направлением силы, действующей на пробный заряд. [E] = Н / Кл или В/м.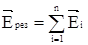 . (6)
. (6)


