Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механические волны. Кинематическое и динамическое уравнения волны.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В широком смысле, под волной понимают процесс распространения в пространстве колебаний или возмущений состояния вещества или поля с течением времени. Выделяют три типа волн: волны на поверхности жидкости, упругие (иначе механические) и электромагнитные. Рассмотрим механические волны, т.е. процессы распространения механических возмущений в упругой среде. Таким образом, в волновом процессе не происходит переноса массы. От частицы к частице передается только колебательное движение, а значит, и энергия.Перенос энергии без переноса вещества – это основное свойство всех волн, независимо от их природы. Волны бывают продольные, если колебания частиц среды происходят вдоль направления распространения, и поперечные, если направление колебаний перпендикулярно вектору скорости Геометрическое место точек (поверхность), до которых колебания дошли к некоторому моменту времени, называется фронтом волны. В зависимости от формы фронта волны бывают: плоские, сферические, цилиндрические и т.д. Поверхность, точки которой имеют одно и то же значение фазы, называется волновой поверхностью. Волновых поверхностей бесчисленное множество, а фронт волны всегда один. УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ Получим уравнение плоской волны в однородной среде вдоль оси 0х, совпадающей с направлением её распространения. Т.к., в этом случае фронт волны перпендикулярен 0х, то смещения s частиц среды будут зависеть только от координаты х и момента времени t, т.е. уравнение волны будет представлять собой функцию – s = f(x,t). Пред-положим, что в точке 0 (рис.1) частица совершает колебания по гармоническому закону: s = Acosωt. s = A cosω(t-τ) (1)
Если обозначить скорость волны через u, то время запаздывания, за которое волна добежит от точки 0 до точки М: τ = х/u, и уравнение колебаний в произвольной точке М на расстоянии х от источника примет вид: s= A cos ω(t-τ) = A cos ω(t - Это и есть искомое уравнение плоской бегущей волны. Здесь: А – амплитуда смещения частиц среды от положения равновесия, ω – циклическая частота колебаний частиц, ω(t - Расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе, называется длиной волны λ (рис.1). Длина волны равна расстоянию, на которое распространяется определенная фаза колебаний за период колебаний частиц среды. Тогда λ = u·T = u /ν. Т.к. ω = 2πν, то (2) можно переписать в виде: s = Acosω(t - Покажем, что скорость распространения волны u – это скорость перемещения фиксированного значения фазы. Положим ω(t – Скорость распространения механических волн зависит от физических свойств среды. Скорость распространения продольных волн определяется формулой: Основные свойства волн: прямолинейность распространения в однородной среде, отражение и преломление на границе раздела сред, дисперсия, интерференция и дифракция. ВОЛНОВОЕ УРАВНЕНИЕ
В трехмерном случае:
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 888; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.156.91 (0.006 с.) |

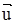 волны. Очевидно, что в случае продольных волн в среде возникают деформации сжатия и разрежения, которые в свою очередь приводят к образованию локальных областей сгущения и разрежения вещества, т.е. области повышенного и пониженного давления. Такие волны могут возникать в любых средах: в газах, жидкостях и твердых телах. Поперечные механические волны обусловлены деформациями сдвига. Это означает, что они могут существовать только в твердых телах.
волны. Очевидно, что в случае продольных волн в среде возникают деформации сжатия и разрежения, которые в свою очередь приводят к образованию локальных областей сгущения и разрежения вещества, т.е. области повышенного и пониженного давления. Такие волны могут возникать в любых средах: в газах, жидкостях и твердых телах. Поперечные механические волны обусловлены деформациями сдвига. Это означает, что они могут существовать только в твердых телах.
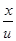 ). (2)
). (2)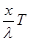 ) = Acos2π(v t -
) = Acos2π(v t - 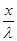 ) = Acos(ωt - 2π
) = Acos(ωt - 2π 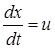 (С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью.
(С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью. . Для поперечных волн –
. Для поперечных волн –  . Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.
. Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.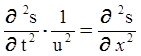 ;
; 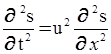 . (5)
. (5)