
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонические колебания. Дифференциальное и кинематическое уравнения незатухающего гармонического колебания. Скорость и ускорение тела при гармоническом колебании.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Получим закон гармонических колебаний на примере механического движения механических колебаний. Это вид колебаний, при котором тело поочерёдно и многократно совершает отклонения от своего положения равновесия в одну и другую сторону.
Примем за начало отсчета точку 0, в которой находится центр шарика в равновесном состоянии системы, т.е. при отсутствии деформации в пружине. Пусть в момент времени t шарик находится на расстоянии s от положения равновесия. Характер движения в данный момент времени определяется равнодействующей приложенных к шарику сил:
В соответствии со 2-ым законом Ньютона эта сила сообщает шарику ускорение
Это дифференциальное уравнение второго порядка с постоянными коэффициентами. s= С1cosω0t + C2sinω0t. (5)
Для любых С1 и С2 всегда можно подобрать другие произвольные постоянные А и φ0 такие, что С1 = Аsin φ0,1 а С2 = Аcosφ0,1, Тогда общее решение (5) примет вид:
s= А(sin φ0,1·cosω0t + cosφ0,1·sinω0t) = Аsin(ω0t + φ0,1). (6)
Если выражения для С1 и C2 поменять местами (С1 = Аcosφ0,2 а С2 = Аsin φ0,2), то общее решение будет иметь вид:
s= А(cos φ0,2·cosω0t + sinφ0,2·sinω0t) = Аcos(ω0t + φ0,2). (7)
Данные функции (6) и (7) и есть искомые кинематические уравнения гармонического колебания. Аргумент этой функции (w0t + φ0) называется фазой колебания; j0 – постоянная составляющая фазы называется начальной фазой;
Получим уравнения, описывающие изменения скорости и ускорения тела, совершающего гармонические колебания. Пусть s = Аcos(ω0t + φ0), тогда:
Как видно, скорость и ускорение тоже изменяются по гармоническим законам, но скорость опережает по фазе смещение на p/2, а ускорение на p (рис.3), т.е. ускорение находится в противофазе со смещением. В целом, тела, на которые действуют равнодейству-ющие вида F = -ks (такие силы называются квазиупругими), будут совершать гармонические колебания.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.34.50 (0.008 с.) |

 Рассмотрим колебания пружинного маятника вдоль горизонтальной оси при отсутствии силы сопротивления. Пружинный маятник представляет собой массивный шарик массой m, прикрепленный к пружине с ничтожно малой массой и жесткостью k. Другой конец пружины закреплен неподвижно. Если вывести шарик из равновесия и отпустить, то под воздействием силы упругости деформированной пружины система пружина–шарик придет в колебательное движение. Положение шарика на оси будем определять смещением s, т.е. расстоянием от положения равновесия до шарика (рис.1). Наша цель решить основную задачу механики – найти ответ на вопрос: где будет находиться тело в произвольный момент времени t, т.е. найти вид функции s = f(t)?
Рассмотрим колебания пружинного маятника вдоль горизонтальной оси при отсутствии силы сопротивления. Пружинный маятник представляет собой массивный шарик массой m, прикрепленный к пружине с ничтожно малой массой и жесткостью k. Другой конец пружины закреплен неподвижно. Если вывести шарик из равновесия и отпустить, то под воздействием силы упругости деформированной пружины система пружина–шарик придет в колебательное движение. Положение шарика на оси будем определять смещением s, т.е. расстоянием от положения равновесия до шарика (рис.1). Наша цель решить основную задачу механики – найти ответ на вопрос: где будет находиться тело в произвольный момент времени t, т.е. найти вид функции s = f(t)? . Т.к. трение по условию отсутствует, а сила тяжести
. Т.к. трение по условию отсутствует, а сила тяжести  перпендикулярна стержню, то характер движения будет определяться только силой упругости деформированной пружины:
перпендикулярна стержню, то характер движения будет определяться только силой упругости деформированной пружины: = ma (1)
= ma (1) , тогда в скалярном виде (1) можно записать:
, тогда в скалярном виде (1) можно записать: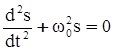 или
или  . (4)
. (4) – собственная циклическая (круговая) частота колебаний данного пружинного маятника (
– собственная циклическая (круговая) частота колебаний данного пружинного маятника ( ,
, 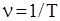 , тогда
, тогда  ); А – амплитуда колебаний, в данном случае максимальное значение смещения s. В общем случае, амплитуда А – это наибольшее значение величины, изменение которой с течением времени выбрали для описания изучаемых колебаний. Графики гармонического колебания представляют собой синусоиды (рис.2):
); А – амплитуда колебаний, в данном случае максимальное значение смещения s. В общем случае, амплитуда А – это наибольшее значение величины, изменение которой с течением времени выбрали для описания изучаемых колебаний. Графики гармонического колебания представляют собой синусоиды (рис.2):
 , (8)
, (8) . (9)
. (9)


