
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебания, которые совершаются под воздействием переменной силы, называются вынужденными.Содержание книги
Поиск на нашем сайте
Рассмотрим колебания под воздействием вынуждающей силы, изменяющейся по гармоническому закону:
F = F○соsω в t. (22)
С учетом квазиупругой силы (1) и силы сопротивления (13) дифференциальное уравнение вынужденных колебаний запишется:
Разделив правую и левую часть на m, и обозначив:
Решением этого уравнения будет функция:
s = Acos(ω в t + φ0). (25)
Это уравнение установившихся вынужденных колебаний. Здесь:
Как видно из (25), колебания, происходящие под воздействием гармонической вынуждающей силы спустя некоторое время, тоже становятся гармоническими (рис. 6). Их частота равна частоте вынуждающей силы ω в. Из выражения (26) для амплитуды видно, что ее значение зависит от соотношения частоты вынуждающей силы ωв и собственной частоты колебательной системы ωо. Очевидно, если подкоренное выражение
Амплитуда при этом достигает значения:
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебательной сис-темы получило название резонанса, а соответствующая частота вынуждающей силы – резонансной частотой колебаний. Приведенные на рис.7 резонансные кривые, отличаются значением коэффициента затухания, действующего в колебательной системе. С уменьшением значения β, резонансные кривые становятся все острее, а величина Арез все больше. Теоретически при β → 0 частота ωрез→ ω0, а амплитуда А → ∞. Как показывает сопоставление (22) и (25), вынужденные колебания тела отстают по фазе от колебаний вынуждающей силы на φ0. График зависимости φ 0 от ωв при различных значениях β. Резонанс может иметь как полезные, так и вредные последствия. В одних случаях он может вызвать разрушение, и это приходится учитывать при конструировании мостов, самолетов, высотных домов. В других случаях, наоборот, стремятся создать условия для резонанса, например, при изготовлении музыкальных инструментов. Автоколебания (качели, часы, электрический колебательный контур) – незатухающие колебания, поддерживаемые внешним источником энергии. Причем поступление энергии регулируется самой колебательной системой. Параметрические колебания – это колебания, возбуждаемые путем периодического изменения параметров колебательной системы. Пример: шарик на нити, длина которой периодически меняется.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.247.221 (0.006 с.) |

 . (23)
. (23)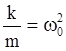 ,
,  ,
,  , после перегруппировки слагаемых, получим неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами:
, после перегруппировки слагаемых, получим неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами: . (24)
. (24)
 , (26)
, (26) . (27)
. (27) будет минимально, то амплитуда вынужденных колебаний достигнет своего максимального значения. Исследование на экстремум дает: -2(ω02 – ωв2) ·2ωв + 8β2ωв = 0, ωв2 - ω02 + 2β2 = 0, что будет иметь место, если
будет минимально, то амплитуда вынужденных колебаний достигнет своего максимального значения. Исследование на экстремум дает: -2(ω02 – ωв2) ·2ωв + 8β2ωв = 0, ωв2 - ω02 + 2β2 = 0, что будет иметь место, если . (28)
. (28) Арез =
Арез =  . (29)
. (29)


