
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент импульса тела остается неизменным, если суммарный момент всех внешних сил действующих на тело равен нулю – это закон сохранения момента импульса.Содержание книги
Поиск на нашем сайте
Для системы из N тел, которые вращаются вокруг общей оси, закон сохранения импульса записывается в виде:
Из определения момента инерции тел в общем виде:
следует, что эта величина является аддитивной. Это означает, что моменты инерции тел в некоторых случаях можно найти интегрированием исходя из геометрических соображений.
Без выводов запишем: а) шар радиусом R и массой m, относительно оси, проходящей через его центр – б) полый тонкостенный цилиндр радиусом R и массой m, относительно его геометрической оси, параллельной образующей –
Согласно теореме Штейнера момент инерции тела – J относительно любой оси, параллельной оси проходящей через центр масс этого тела –
где J0 – момент инерции тела относительно оси, проходящей через центр масс, d – расстояние между осями. Например, если ось вращения проходит через конец стержня,
то
Механические колебания. Основные характеристики колебательного движения (смещение, амплитуда, частота, период, фаза). Колебаниями называется вид движения физических тел или такие процессы, для которых характерна та или иная степень повторяемости во времени. Например: движения маятника и гитарной струны, голосовых связок и барабанной перепонки уха, колебания температуры воздуха и напряжения в электросети. Колебания имеют различное происхождение, разную физическую природу: колебания механические, тепловые, электрические, электромагнитные, оптические и др. Если повторяемость состояний колеблющейся системы имеет произвольный характер - апериодические. Колебания, для которых последовательность состояний системы повторяется через равные промежутки времени, называются периодическими. В зависимости от характера воздействия, оказываемого на колебательную систему извне, различают: свободные (или собственные) колебания и колебания вынужденные. По этому признаку различают еще автоколебания и параметрические колебания. Свободные - колебания, которые совершаются за счет внутренних сил системы, предоставленной самой себе после того, как ей был сообщён внешний первоначальный толчок, породивший эти колебания. Например, шарик на нити. Вынужденные - колебания, которые совершаются под постоянным воздействием внешней переменной силы. Например, колебания моста, когда по нему идут пешеходы. Если с течением времени запас энергии колебательной системы не меняется, то такое колебание называется незатухающим. Если же эта энергия уменьшается, то – затухающим. Независимо от природы, все виды колебательного движения имеют общие закономерности, т.е. протекают по одним и тем же законам и характеризуются одними и теми же параметрами: периодом Т, частотой ν, амплитудой А и фазой φ. Период - время одного полного колебания. За период тело проходит расстояние, равное 4-м амплитудам Линейная частота – число колебаний за 1 секунду. Герц. – период и линейная частота взаимообратные величины. Математический маятник с короткой нитью имеет большую линейную частоту колебаний, чем математический маятник с длинной нитью. Циклическая или круговая частота – число колебаний за 2? Секунд.. А=Хmax [м] – амплитуда – модуль максимального смещения тела от положения равновесия. 6. Фаза – физическая величина, описывающая состояние колебательной системы в данный момент времени. Закон колебательного движения – это уравнение, которое показывает, как с течением времени изменяются параметры, описывающие состояния колеблющегося тела. Простейшими являются гармонические колебания, для которых изменение величин, описывающих состояние системы, происходит по закону синуса или косинуса.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.170.80 (0.008 с.) |

 . (29)
. (29) (30)
(30) В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d << l относительно оси
В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d << l относительно оси  проходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.
проходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.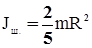 (31)
(31) (32)
(32) , (33)
, (33)
 (34)
(34)


