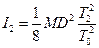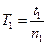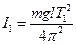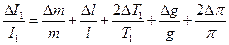Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ускорения силы тяжести по способу Бесселя.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Приборы и принадлежности: маятник, секундомер.
Краткая теория. Период колебания математического маятника определяется формулой
где 1 - длина маятника, g - ускорение силы тяжести. Предположим, что маятник сначала имеет длину (l + h) колеблется с периодом:
Затем длина его уменьшится на h и новый период колебания будет:
Возведем обе части формул (2) и(3) в квадрат и полученные равенства разрешим относительно 1, приравниваем соответствующие части уравнений и разрешаем получившиеся уравнения относительно g. Получаем:
Этой формулой мы воспользуемся для определения g. Эта формула удобна тем, что длину маятника нам определять не нужно. Период Т1| и Т2 определяется секундомером или при помощи часов. Разность длин маятников измеряется линейкой реохорда.
Порядок выполнения работы 1. маятнику задается произвольная длина (1+h) 2. маятник выводится из положения равновесия и, предоставленный самому себе, начинает качаться. Когда маятник совершит 40 колебаний, останавливают секундомер и вычисляют период T1 опыт повторяется не менее трех раз. 3. затем поднимают шарик на высоту h, которую измеряют 4. определяют тем же способом период короткого маятника Т2; Необходимо помнить, что формула (1) справедлива только для малых отклонений маятника от положения равновесия (2-3 см) Из формулы (4) видно, что выгодно брать для h большое значение, чтобы периоды T1 и Т2 значительно отличались друг от друга. 5. все данные наблюдений и вычислений заносят в следующую таблицу:
Вычисления g производится по преобразованной формуле:
Примечание: При выполнении этой работы следует определение длины и промежутков времени делать как можно точнее, т.к. даже малая ошибка сильно искажает результат.
Контрольные вопросы 1. Как изменится ускорение силы тяжести от широты места?
Каким образом можно изменить период колебаний маятника не изменяя его длины?
Лабораторная работа №7. Физический маятник.
Цель работы: знакомство с физическим маятником и использование его для определения ускорения свободного падения. Необходимые приборы: физический маятник, секундомер, штангенциркуль, трехгранная призма, линейка. Введение Период колебания физического маятника при малых амплитудах равен: вращения, М — его масса, а - расстояние от оси вращения до центра тяжести маятника, g — ускорение свободного падения. Применив теорему Штейнера для определения момента инерции I, из уравнения (1) получим:
В работе используется физический маятник, состоящий из металлическогостержня ссантиметровыми делениямии двух массивных грузов, которые можно передвигатьвдоль стержня ( puc. l).
а2 а1
На стержне укреплены две опорные призмы О1 иО2, служащие для подвешивания маятника. Определение ускорения свободного падения.
Для определения ускорения свободного падения с помощью физического маятника, следует определить период колебания маятник относительно оси, совпадающей с ребром призмы O1, который по формуле (2) будет равен:
Выполнение работы: 1.Снимите маятник и поместите его на ребре вспомогательной трехгранной призмы. 2.Перемещая точку опоры, добейтесь равновесия маятника. В этом случае точка опоры определяет положение центра тяжести маятника. 3.Измерьте расстояние от центра тяжести до ребра призмы О1 (а1) и ребра призмы О2 (а2). 4.Подвесьте маятник за призму О1, и отклонив маятник на небольшой |угол определите время 40 колебаний. Подсчитайте период Т1. 5.Переверните маятник и аналогично п.4, рассчитайте период Т2; 6.По формуле (5) подсчитайте ускорение. Результат занесите в таблицу
Лабораторная работа № 9. ПРОВЕРКА ТЕОРИИ ШТЕЙНЕРА. Краткая теория. Целью этой работы является экспериментальная проверка теоремы Штейнера:
I1= I2 + ma2 (1), где I1- момент инерции тела с массой m относительно произвольной оси O1, I2- момент инерции того же тела относительно оси О2 параллельной оси O1 и проходящей через его центр инерции; а - расстояние между осями. Для определения момента инерции I1используется формула для периода колебаний физического маятника:
Момент инерции I2определяется при помощи формулы для периода крутильных колебаний:
где f- крутильный момент подвеса. Чтобы исключить f из формулы (3) измеряется период Т0 крутильных колебаний другого тела, обладающего известным моментом инерции 10 и подвешенного на той же нити. Используя формулу (3), получим:
В качестве вспомогательного тела применяется диск, момент инерции которого относительно оси симметрии, перпендикулярно к его плоскости, определяется по формуле:
где М - масса диска, D - диаметр диска.
ОПИСАНИЕ УСТАНОВКИ. В качестве исследуемого тела используется стержень с призмами на концах для подвеса. Для изучения его крутильных колебаний относительно оси, проходящей через центр инерции стержня и перпендикулярной к образующей стержня (ось 02), стержень навинчивается на винт, прикрепленный к нити подвеса. Для изучения колебаний стержня как физического маятника, стержень с помощью призм устанавливается в желобок вилки, закрепленной в штативе. Таким образом ось колебаний физического маятника (ось O1) проходит через ребро призм и перпендикулярно к образующей стержня (как и ось О2). ВЫПОЛНЕНИЕ РАБОТЫ. 1. Взвешиваем на технических весах и определяем массу m стержня и М-диска. 2. С помощью штангенциркуля определить диаметр D диска и расстояние l между ребрами призм и центром стержня. 3. Стержень навинчивается на винт подвеса и приводится в состояние колебательного движения (крутильных колебаний). Секундомером измеряют время t2 количества колебаний n2=25. Определяется период крутильных колебаний по формуле:
Опыт повторить три раза.
Затем на винт подвеса навинчивается диск и измеряется его период колебаний T0 (как у стержня - три серии по 25 колебаний). Согласно формулам (4) и (5) получим:
4. Ребро призмы стержня установить в желобок вилки и привести стержень в колебание. Секундомером измеряется время t1 некоторого количества n1 (n1 =25) полных колебаний и находим период колебаний физического маятника:
Опыт повторяют три раза. Из формулы (2) следует:
5.После вычисления погрешностей, проверить справедливость равенства (1).
Литература:
1. Савельев И.В., Курс общей физики; т.1, § 39 (Момент инерции, стр. 140-144), М, 1982г. 2. Стрелков СП., Механика, § 59, стр. 211-215, М, 1975г.
ЛАБОРАТОРНАЯ РАБОТА № 8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1083; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

 (1)
(1) (2)
(2) (3)
(3) (4)
(4)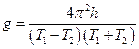 (6)
(6)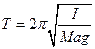 ( 1), где I момент инерции маятника относительно оси
( 1), где I момент инерции маятника относительно оси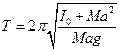 (2)
(2)
 . Рис.1 О2 Р2 О1 Р1
. Рис.1 О2 Р2 О1 Р1

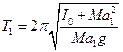 (3) и период колебаний относительно оси, совпадающей с ребром призмы О2, который будет по (2) равен:
(3) и период колебаний относительно оси, совпадающей с ребром призмы О2, который будет по (2) равен: 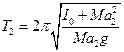 (4). Из формул (3) и (4) получается выражение для определения ускорения свободного падения:
(4). Из формул (3) и (4) получается выражение для определения ускорения свободного падения: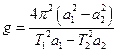 (5)
(5)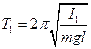 (2),
(2),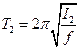 (3),
(3),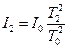 (4)
(4)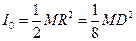 (5),
(5),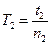 (6),
(6),