Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цель работы: изучить нониусы.Содержание книги Поиск на нашем сайте
Лабораторная работа №1 Изучение нониусов. Цель работы: изучить нониусы. Приборы и принадлежности: модель нониуса, штангенциркуль, микрометр, гониометр, тела для измерения. Нониус. Нониусом называется дополнение к обычному масштабу (линейному или круговому), позволяющее повысить точность измерения с данным масштабом в 10-20 раз. Техника непосредственного измерения длин и углов достигла к настоящему времени большого совершенства. Сконструирован ряд специальных приборов, так называемых компараторов, позволяющих замерять длину с точностью до 1 микрона.(1 микрон = 10-4 ). Большинство из них основано на применении микроскопа и некоторых других оптических приспособлений. Но при этом почти всегда отсчетные приспособления снабжаются нониусами или микрометрами. В ряде случаев требуется относительная точность измерения длины бывает такова, что можно удовлетвориться абсолютной точностью в сотые или даже в десятые доли миллиметра, а для углов минутами или долями минут. В этом случае можно для измерения пользоваться обычными масштабными линейками и угломерами, снабженными нониусами. Примерами таких являются штангенциркуль, гониометр, микрометр. Линейный нониус. Он представляет собой небольшую линейку, скользящую вдоль масштаба. На этой линейке нанесена маленькая шкала, состоящая вдоль делений. Суммарная длина всех ее mx делений равна (m-1), наименьшим делением основного масштаба, т.е. mx=(m-1)y, где х - длина деления нониуса, а у – длина наименьшего деления масштаба, которая, вообще говоря, может иметь любое значение. Отсюда Рассмотрим теперь процесс измерения при помощи линейного нониуса. Пусть L-измеряемый отрезок. Совместим нулевое деление основного масштаба с его началом. Пусть при этом конец его окажется между k и k-1 делением этого масштаба. Тогда можно написать: L=ky+ ∆L Где ∆L-неизвестная пока еще доля k-го деления масштаба. Приложим теперь к концу отрезка наш нониус так, чтобы нуль нониуса совпадал с концом того отрезка, т.к. деления нониуса не равны делениям масштаба, то обязательно найдется на нем такое деление n, которое будет ближе всего подходить к соответствующему k+ n делению масштаба. ∆L=ny-nx=n(y-x)=n∆х ð L=ky=n∆х ð Что можно сформулировать следующим образом: Длина отрезка, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба. Погрешность, которая может возникнуть при таком методе отсчета, будет обуславливаться неточным совпадением n деления нониуса с k + n делением масштаба, и величина ее не будет превышать, очевидно, Длина делений масштаба и число делений нониуса, а следовательно и точность нониуса, бывают самые разнообразные. Ниже приведенная таблица дает наиболее часто встречающиеся сочетания:
Круговой нониус В принципе он ничем не отличается от линейного. Он представляет собой небольшую дуговую линейку, скользящую вдоль круга (лимба), разделённого на градусы или на еще более мелкие деления. На линейке нанесены деления также в количестве т, общая длина которых равна (т - 1) делениям лимба, т.е. ma=(m - 1)ß, где а и ß - выраженные в градусах или минутах цены деления нониуса (а) и наименьшего деления лимба (ß). Отсчитываемые от нуля углы будут вычисляться, очевидно, по формуле: φ = kß + п∆а Часто круговые нониусы в приборах, в которых необходимо отсчитывать углы в обоих направлениях (по часовой стрелке я против, нее), состоят из двух совершенно одинаковых шкал, расположенных по обе стороны от нуля. Легко сообразить, что при отсчетах следует всегда пользоваться той шкалой, которая идет впереди по направлению отсчетов. Микрометр Микрометр служит для измерения диаметра проволок, небольших толщин пластинок и т.п. Он имеет вид тисков, в которых измеряемый объект зажимается с помощью винта. Ход винта обыкновенно бывает 1 мм или 0,5 мм. На стержне винта укреплен барабан с нанесенной на нем шкалой, имеющей 50 или 25 делений. При зажатом винте нуль барабана стоит напротив нуля линейно линейной шкалы. Измеряемый объект помещают между винтом и противоположным ему упором. Затем, вращая винт, доводят его до соприкосновения с исследуемым предметом. На линейной шкале отсчитывают миллиметры, а по шкале барабана - сотые доли миллиметра. Главным источником ошибок является неравномерность нажатия винта на измеряемый предмет. Для устранения этого недостатка современные микрометры снабжаются специальным приспособлением, недопускающим слишком сильное нажатие. Действие подобных приспособлений основано на трении, возникающим между стержнем винта и рукояткой, поворачивающей винт. Упражнение 1 Задание: измерять длину трех тел. Взяв винт за головку, выдвигают его настолько, чтобы измеряемый предмет мог переместиться между неподвижным стержнем и стержнем винта. Держа предмет перпендикулярно к длине стержней, вращают винт до соприкосновения стержня с предметом до первого щелчка винта Делают отчет по нониусу. Результаты записывают.
Штангенциркуль. Штангенциркуль состоит из разделенного на миллиметры масштаба, вдоль которого может перемещаться перпендикулярно его длине ножка с зажимным винтом, служащим для ее закрепления, в ее обойме против делений масштаба сделан вырез, на скошенном краю которого, прилегающим к масштабу, нанесен нониус. Когда ножки штангенциркуля сдвинуты вплотную, нуль нониуса совпадает с нулем масштаба. Неподвижная ножка, укрепленная в начале масштаба, так же перпендикулярна его длине, она служит упором для измеряемого тела. Части обеих ножек служат для измерения внутренних размеров тел. Упражнение 2. Задание: определение объема трубки. Для определения объема трубки надо знать ее геометрические размеры - длину, внутренний и внешний диаметры. Измерения проводят несколько раз, повернув перед каждым измерением трубку около ее оси на некоторый угол. Из всех полученных результатов берут среднее арифметическое. Из результатов измерений по элементарным геометрическим формулам вычисляют объем трубки. Результаты записывают. Измерение углов, наряду с измерением длин, относится к числу наиболее распространенных измерений не только в физическом эксперименте, но и в целом ряде других смежных дисциплин. Приборы, служащие для этих измерений, состоят обыкновенно из двух основных частей: лимба, по которому производят отсчеты направлений двух радиусов, заключающих между собой искомый угол, и визирного приспособления, при помощи которого определяют направления этих радиусов. Визирное приспособление имеет возможность вращаться вокруг оси, проходящей через центр лимба, и направление его при помощи скрепленного с ним указателя отсчитывается по шкале лимба. Искомый угол находится затем как разность двух отчетов соответствующих положений визира. Иногда встречается обратное положение лимба и указателя: лимб, скрепленный с визиром, вращается вместе с ним, положение его отсчитывается при помощи неподвижного указателя. Для точного отсчета направлений визира по шкале лимба применяются круговые нониусы. Особенно важно значение в этих приборах имеет правильная центровка, т.е. совмещение оси вращения визира с центром отсчета. При отсутствии должной центровки величины углов, отсчитываемых по лимбу, не будет соответствовать своим истинным значениям. Это может быть устранено при помощи двух нониусов (с преувеличенным и приуменьшенным значениями). Где берется среднее значение, не зависящее от эксцентриситета установки. Гониометр Он состоит из горизонтального лимба, укрепленного на штативе. Вокруг оси, проходящей через центр лимба, вращается так называемая: алидада - планка с укрепленными на концах диоптрами - вертикальными продолговатыми щелями, в одной из которых, более широкой (объектной) натянута нить. Плоскость, проводящая через эту нить в середине узкой (глазной) щели, является визирной плоскостью. На алидаде нанесены деления нониуса, при помощи которых отсчитывается ее положение. Упражнение 3 Принадлежности: гониометр. Здание: измерение углов. Установив прибор, наводят алидаду на одну из меток, наклеенных на стенах лаборатории так, чтобы визирная нить алидады совпадала с этой меткой (глаз должен находится непосредственно вблизи глазной щели). ЛАБОРАТОРНАЯ РАБОТА N 4 Определение скорости при помощи баллистического маятника Приборы и принадлежности: баллистический маятник со шкалой и духовое ружье. Введение. Два неупругих тела после соударения движутся вместе с одинаковой скоростью. Если тело массы М покоится, а тело массы m движется со скоростью v, то после неупругого соударения оба тела будут перемещаться с общей скоростью v1. На основании закона сохранения количества движения в этом случае имеем mv = (M+m)V1 т.е. количество движения до и после соударения остается неизменным. Закон сохранения количества движения положен в основу измерений скоростей быстро движущихся тел, в частности пули, при помощи баллистического маятника. Баллистический маятник представляет собой вертикально подвешенный тяжелый ящик С, в стенку которого производится выстрел (рис. 1). Ящик заполняется песком или ватой для того, чтобы пуля застряла в нем. При попадании пули массой М, обладающей скоростью v1, в неподвижный ящик массой М ящик с пулей приобретает скорость v1 и, следовательно, количество движения выразится соотношением (1). Подвешенный ящик с пулей отклонится от вертикали, на некоторый угол а, а его центр тяжести (С) поднимется на высоту h. В момент максимального отклонения ящика от положения равновесия, когда v1=0, его кинетическая энергия
превращается в потенциальную (M+m)gh. Если пренебречь массой пули по сравнению с массой ящика (m«М), то /////////i////i//t////////fi/////////////i////i//t////////f
Рис.1 Баллистический маятник, применяемый в настоящей работе, представляет собой ящик с ватой, подвешенный на четырех нитях. Дно ящика снабжено указателем, который при отклонении ящика, в момент выстрела, перемещается вдоль горизонтальной шкалы. Благодаря такому устройству, можно заменить сложное измерение высоты подъема ящика h более простым измерением — горизонтальным перемещением S (рис.1). Из рис. 1 видно, что треугольник АКВ подобен треугольнику ODB, а на основании подобия этих треугольников,
где OD=l- длина нитей, на которых подвешен ящик; AK=S - горизонтальное перемещение; BK=h - высота подъема ящика.
Ввиду малости величины h, DB≈ S2 и тогда соотношение (3) можно записать в виде
откуда
Подставляя значение h в выражение (2), получим окончательную формулу для расчета скорости пули
Порядок выполнения работы 1. Для выстрела берут пять-шесть пуль; каждую пулю взвешивают, вес пули должен отличаться друг от друга не более чем на 0,5%
При этих условиях уравнение (1) примет несколько иной вид: Mv1= mv или
Подставляя сюда значение V1, получаем
2. Производят выстрелы из духового ружья в стенку ящика, при этом отмечается по шкале перемещение S после каждого выстрела. Данные измерений заносят в следующую таблицу:
М = 959г l =265 см ∆M= +-5г ∆ l = + -1см
Обработка результатов измерений
1. Подсчитывают средние значения m и S. 2. По средним значениям m и S и постоянным прибора М и I рассчитывают значение скорости пули v по формуле (4). 3. Подсчитывают погрешность по формуле
Результат измерений записывается в виде V=(.....±......) см/сек.
ЛАБОРАТОРНАЯ РАБОТА № 7(а) Порядок выполнения работы 1. маятнику задается произвольная длина (1+h) 2. маятник выводится из положения равновесия и, предоставленный самому себе, начинает качаться. Когда маятник совершит 40 колебаний, останавливают секундомер и вычисляют период T1 опыт повторяется не менее трех раз. 3. затем поднимают шарик на высоту h, которую измеряют 4. определяют тем же способом период короткого маятника Т2; Необходимо помнить, что формула (1) справедлива только для малых отклонений маятника от положения равновесия (2-3 см) Из формулы (4) видно, что выгодно брать для h большое значение, чтобы периоды T1 и Т2 значительно отличались друг от друга. 5. все данные наблюдений и вычислений заносят в следующую таблицу:
Вычисления g производится по преобразованной формуле:
Примечание: При выполнении этой работы следует определение длины и промежутков времени делать как можно точнее, т.к. даже малая ошибка сильно искажает результат.
Контрольные вопросы 1. Как изменится ускорение силы тяжести от широты места?
Каким образом можно изменить период колебаний маятника не изменяя его длины?
Лабораторная работа №7. Физический маятник.
Цель работы: знакомство с физическим маятником и использование его для определения ускорения свободного падения. Необходимые приборы: физический маятник, секундомер, штангенциркуль, трехгранная призма, линейка. Введение Период колебания физического маятника при малых амплитудах равен: вращения, М — его масса, а - расстояние от оси вращения до центра тяжести маятника, g — ускорение свободного падения. Применив теорему Штейнера для определения момента инерции I, из уравнения (1) получим:
В работе используется физический маятник, состоящий из металлическогостержня ссантиметровыми делениямии двух массивных грузов, которые можно передвигатьвдоль стержня ( puc. l).
а2 а1
На стержне укреплены две опорные призмы О1 иО2, служащие для подвешивания маятника. Определение ускорения свободного падения.
Для определения ускорения свободного падения с помощью физического маятника, следует определить период колебания маятник относительно оси, совпадающей с ребром призмы O1, который по формуле (2) будет равен:
Выполнение работы: 1.Снимите маятник и поместите его на ребре вспомогательной трехгранной призмы. 2.Перемещая точку опоры, добейтесь равновесия маятника. В этом случае точка опоры определяет положение центра тяжести маятника. 3.Измерьте расстояние от центра тяжести до ребра призмы О1 (а1) и ребра призмы О2 (а2). 4.Подвесьте маятник за призму О1, и отклонив маятник на небольшой |угол определите время 40 колебаний. Подсчитайте период Т1. 5.Переверните маятник и аналогично п.4, рассчитайте период Т2; 6.По формуле (5) подсчитайте ускорение. Результат занесите в таблицу
Лабораторная работа № 9. ПРОВЕРКА ТЕОРИИ ШТЕЙНЕРА. Краткая теория. Целью этой работы является экспериментальная проверка теоремы Штейнера:
I1= I2 + ma2 (1), где I1- момент инерции тела с массой m относительно произвольной оси O1, I2- момент инерции того же тела относительно оси О2 параллельной оси O1 и проходящей через его центр инерции; а - расстояние между осями. Для определения момента инерции I1используется формула для периода колебаний физического маятника:
Момент инерции I2определяется при помощи формулы для периода крутильных колебаний:
где f- крутильный момент подвеса. Чтобы исключить f из формулы (3) измеряется период Т0 крутильных колебаний другого тела, обладающего известным моментом инерции 10 и подвешенного на той же нити. Используя формулу (3), получим:
В качестве вспомогательного тела применяется диск, момент инерции которого относительно оси симметрии, перпендикулярно к его плоскости, определяется по формуле:
где М - масса диска, D - диаметр диска.
ОПИСАНИЕ УСТАНОВКИ. В качестве исследуемого тела используется стержень с призмами на концах для подвеса. Для изучения его крутильных колебаний относительно оси, проходящей через центр инерции стержня и перпендикулярной к образующей стержня (ось 02), стержень навинчивается на винт, прикрепленный к нити подвеса. Для изучения колебаний стержня как физического маятника, стержень с помощью призм устанавливается в желобок вилки, закрепленной в штативе. Таким образом ось колебаний физического маятника (ось O1) проходит через ребро призм и перпендикулярно к образующей стержня (как и ось О2). ВЫПОЛНЕНИЕ РАБОТЫ. 1. Взвешиваем на технических весах и определяем массу m стержня и М-диска. 2. С помощью штангенциркуля определить диаметр D диска и расстояние l между ребрами призм и центром стержня. 3. Стержень навинчивается на винт подвеса и приводится в состояние колебательного движения (крутильных колебаний). Секундомером измеряют время t2 количества колебаний n2=25. Определяется период крутильных колебаний по формуле:
Опыт повторить три раза.
Затем на винт подвеса навинчивается диск и измеряется его период колебаний T0 (как у стержня - три серии по 25 колебаний). Согласно формулам (4) и (5) получим:
4. Ребро призмы стержня установить в желобок вилки и привести стержень в колебание. Секундомером измеряется время t1 некоторого количества n1 (n1 =25) полных колебаний и находим период колебаний физического маятника:
Опыт повторяют три раза. Из формулы (2) следует:
5.После вычисления погрешностей, проверить справедливость равенства (1).
Литература:
1. Савельев И.В., Курс общей физики; т.1, § 39 (Момент инерции, стр. 140-144), М, 1982г. 2. Стрелков СП., Механика, § 59, стр. 211-215, М, 1975г.
ЛАБОРАТОРНАЯ РАБОТА № 8
КРАТКАЯ ТЕОРИЯ.
Моментом инерции материальной точки массой m находящейся на расстоянии r от оси вращения, называется произведение масcы этой точки на квадрат расстояния от оси вращения, т.е. Если имеем дело с телом, то моментом инерции его называется сумма моментов инерции всех его точек, т.е. Во вращательном движении момент инерции играет ту же роль, какую в. поступательном движении играет масса. Поэтому определение момента инерции имеет большое практическое значение. Определить момент инерции тела относительно какой-нибудь оси можно путем вычисления, если тело имеет правильную форму и известно распределение массы внутри тела. Но чаще всего приходится определять момент инерции тела относительно какой-нибудь оси опытным путем. В нашей работе для этой цели применяется крестообразный маятник (рис.1). Он представляет собой маховик, с четырьмя взаимно перпендикулярными стержнями, вдоль которых могут перемещаться грузы. Для этих грузов нам и предстоит найти момент инерции. На общей оси маятника находится валик; на валик намотана нить с привязанным грузом. Основное выражение динамики для вращающегося тела выражается так:
где М - момент силы, под влиянием которой тело вращается вокруг оси, I -| момент инерции вращающегося тела,
Из уравнения-(1) имеем:
Таким образом, для определения инерции вращающегося тела нужно знать момент вращающей силы и угловое ускорение тела. Будем искать эти величины.
Привяжем к нити маятника некоторый груз и представим ему возможность падать. Это падение будет равноускоренным. Если высота падения h, а время падения t, то
где а-линейное ускорение. Отсюда: Но с таким ускорением будут двигаться все тела (точки) на поверхности валика. Измерив радиус валика r, можно найти угловое ускорение Е маховика:
Вращающим моментом силы называется произведение силына ее плечо. Напомним, что, плечом называется расстояние от оси вращения до прямой, совпадающей с направлением действия силы. В нашем примере плечо силы равно радиусу валика. Найдем, чему равна сила, вращающая маятник. На груз массы m действуют: I) сила тяжести Р = mg 2) натяжение нити (силы противоположного направления) PH Результирующая сила: F=ma. По второму закону Ньютона, эта сила, действуя на груз массы mбудет перемещать его с ускорением a, т.е.
Отсюда: Но натяжение нити PH численно равно, той силе, которая приводит во вращение крестообразный маятник. Поэтому момент этой силы
Подставив значения М и
ВЫПОЛНЕНИЕ РАБОТЫ. I. Находят момент инерции маятника I1 2.:На стержни маятника на одинаковом расстоянии R от оси вращения, надевают четыре одинаковых груза, каждый массовый момент которого неизвестен и подлежит определению. Затем находят момент инерции всей системы I2. 3. Очевидно, что момент инерции четырех надетых на стержни грузов будет равен 4. Принимая надетые на крестовину грузы за материальные точки, находят их момент инерции I1путем вычисления
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. I. К нити, намотанной на валик, подвесить груз массы m. 2. Нижний обрез груза совместить с верхним делением шкалы. 3. Одновременно отпустить груз и включить секундомер. В тот момент, когда груз ударится о подставку шкалы, выключить секундомер и записать время падения груза. Определение времени t| производится3-5 раз. Определяем tср. 4. Вычислить линейное ускорение груза 5. На стержни маятника надеть четыре груза равной массы m нa одинаковом R расстоянии от оси вращения. 6. Выполнив п.п. 3, вычислить затем по формуле момент инерции всей вращающейся системы
7. Принимая грузы на стержнях за материальные точки, вычислить, их момент инерции по формуле:
где R среднее расстояние груза от оси вращения. 8. Сравнить результаты измерений, полученные по формулам (6) и (7) Данные измерений заносят в таблиц:
m - масса движущегося груза r - радиус валика h- путь, проходимый падающим телом m1- масса исследуемого груза R- расстояние между центром дополнительного груза и осью вращения g - ускорение свободного падения (g=9,8 м/с2);
Рис.2
Контрольные вопросы
Литература Лабораторная работа №1 Изучение нониусов. Цель работы: изучить нониусы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1853; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.140 (0.01 с.) |

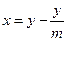 , а разность в длине делений шкалы и нониуса, который называется точностью нониуса, равна
, а разность в длине делений шкалы и нониуса, который называется точностью нониуса, равна 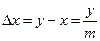 . Эта величина, как мы скоро увидим, и определяет собой максимальную погрешность нониуса.
. Эта величина, как мы скоро увидим, и определяет собой максимальную погрешность нониуса.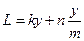
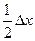 , ибо при большем несовпадении этих делений одно из соседних делений (справа или слева) имело бы несовпадение, меньше чем
, ибо при большем несовпадении этих делений одно из соседних делений (справа или слева) имело бы несовпадение, меньше чем 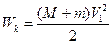
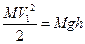 Описание аппаратуры и метода измерения
Описание аппаратуры и метода измерения
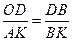 (3)
(3)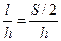
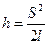
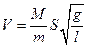 (4)
(4)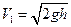
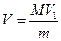
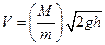 (2)
(2)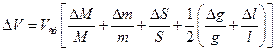
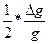 - пренебречь.
- пренебречь.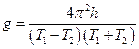 (6)
(6)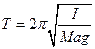 ( 1), где I момент инерции маятника относительно оси
( 1), где I момент инерции маятника относительно оси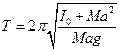 (2)
(2)
 . Рис.1 О2 Р2 О1 Р1
. Рис.1 О2 Р2 О1 Р1

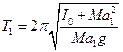 (3) и период колебаний относительно оси, совпадающей с ребром призмы О2, который будет по (2) равен:
(3) и период колебаний относительно оси, совпадающей с ребром призмы О2, который будет по (2) равен: 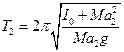 (4). Из формул (3) и (4) получается выражение для определения ускорения свободного падения:
(4). Из формул (3) и (4) получается выражение для определения ускорения свободного падения: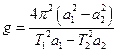 (5)
(5)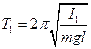 (2),
(2),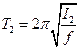 (3),
(3),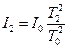 (4)
(4)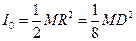 (5),
(5),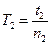 (6),
(6),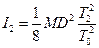
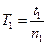
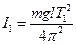
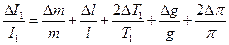
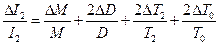
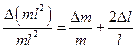
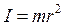
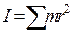 ,
,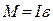 (1)
(1)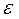 - угловое ускорение тела.
- угловое ускорение тела.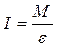 (2)
(2)
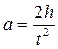
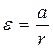 (3)
(3)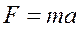
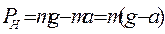
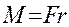
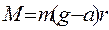 ;
; 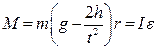 (4)
(4)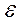 из формул (3) л (4) в формулу (2), получим величину момента инерции вращающегося маятника:
из формул (3) л (4) в формулу (2), получим величину момента инерции вращающегося маятника: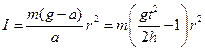 (5)
(5)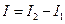
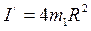 ;
; 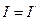
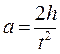 . Затем по формуле (5) вычислить момент инерции маятника (предварительно измерить; радиус валика r).
. Затем по формуле (5) вычислить момент инерции маятника (предварительно измерить; радиус валика r).
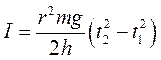 (6)
(6) ; (7)
; (7)
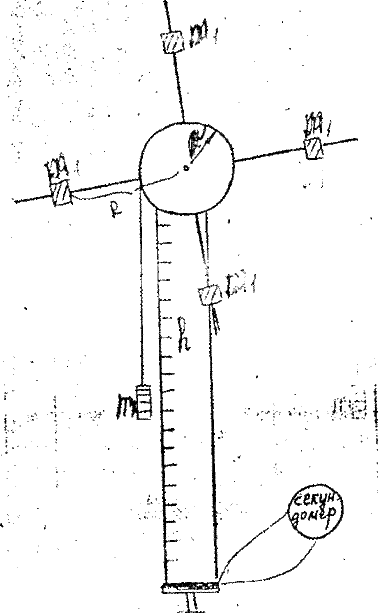 Рис.1
Рис.1