
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приборы и принадлежности: модель нониуса, штангенциркуль, микрометр, гониометр, тела для измерения.Содержание книги
Поиск на нашем сайте Нониус. Нониусом называется дополнение к обычному масштабу (линейному или круговому), позволяющее повысить точность измерения с данным масштабом в 10-20 раз. Техника непосредственного измерения длин и углов достигла к настоящему времени большого совершенства. Сконструирован ряд специальных приборов, так называемых компараторов, позволяющих замерять длину с точностью до 1 микрона.(1 микрон = 10-4 ). Большинство из них основано на применении микроскопа и некоторых других оптических приспособлений. Но при этом почти всегда отсчетные приспособления снабжаются нониусами или микрометрами. В ряде случаев требуется относительная точность измерения длины бывает такова, что можно удовлетвориться абсолютной точностью в сотые или даже в десятые доли миллиметра, а для углов минутами или долями минут. В этом случае можно для измерения пользоваться обычными масштабными линейками и угломерами, снабженными нониусами. Примерами таких являются штангенциркуль, гониометр, микрометр. Линейный нониус. Он представляет собой небольшую линейку, скользящую вдоль масштаба. На этой линейке нанесена маленькая шкала, состоящая вдоль делений. Суммарная длина всех ее mx делений равна (m-1), наименьшим делением основного масштаба, т.е. mx=(m-1)y, где х - длина деления нониуса, а у – длина наименьшего деления масштаба, которая, вообще говоря, может иметь любое значение. Отсюда Рассмотрим теперь процесс измерения при помощи линейного нониуса. Пусть L-измеряемый отрезок. Совместим нулевое деление основного масштаба с его началом. Пусть при этом конец его окажется между k и k-1 делением этого масштаба. Тогда можно написать: L=ky+ ∆L Где ∆L-неизвестная пока еще доля k-го деления масштаба. Приложим теперь к концу отрезка наш нониус так, чтобы нуль нониуса совпадал с концом того отрезка, т.к. деления нониуса не равны делениям масштаба, то обязательно найдется на нем такое деление n, которое будет ближе всего подходить к соответствующему k+ n делению масштаба. ∆L=ny-nx=n(y-x)=n∆х ð L=ky=n∆х ð Что можно сформулировать следующим образом: Длина отрезка, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба. Погрешность, которая может возникнуть при таком методе отсчета, будет обуславливаться неточным совпадением n деления нониуса с k + n делением масштаба, и величина ее не будет превышать, очевидно, Длина делений масштаба и число делений нониуса, а следовательно и точность нониуса, бывают самые разнообразные. Ниже приведенная таблица дает наиболее часто встречающиеся сочетания:
Круговой нониус В принципе он ничем не отличается от линейного. Он представляет собой небольшую дуговую линейку, скользящую вдоль круга (лимба), разделённого на градусы или на еще более мелкие деления. На линейке нанесены деления также в количестве т, общая длина которых равна (т - 1) делениям лимба, т.е. ma=(m - 1)ß, где а и ß - выраженные в градусах или минутах цены деления нониуса (а) и наименьшего деления лимба (ß). Отсчитываемые от нуля углы будут вычисляться, очевидно, по формуле: φ = kß + п∆а Часто круговые нониусы в приборах, в которых необходимо отсчитывать углы в обоих направлениях (по часовой стрелке я против, нее), состоят из двух совершенно одинаковых шкал, расположенных по обе стороны от нуля. Легко сообразить, что при отсчетах следует всегда пользоваться той шкалой, которая идет впереди по направлению отсчетов. Из числа наиболее часто встречающихся круговых нониусов укажем Следующие:
Микрометр Микрометр служит для измерения диаметра проволок, небольших толщин пластинок и т.п. Он имеет вид тисков, в которых измеряемый объект зажимается с помощью винта. Ход винта обыкновенно бывает 1 мм или 0,5 мм. На стержне винта укреплен барабан с нанесенной на нем шкалой, имеющей 50 или 25 делений. При зажатом винте нуль барабана стоит напротив нуля линейно линейной шкалы. Измеряемый объект помещают между винтом и противоположным ему упором. Затем, вращая винт, доводят его до соприкосновения с исследуемым предметом. На линейной шкале отсчитывают миллиметры, а по шкале барабана - сотые доли миллиметра. Главным источником ошибок является неравномерность нажатия винта на измеряемый предмет. Для устранения этого недостатка современные микрометры снабжаются специальным приспособлением, недопускающим слишком сильное нажатие. Действие подобных приспособлений основано на трении, возникающим между стержнем винта и рукояткой, поворачивающей винт. Упражнение 1
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

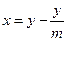 , а разность в длине делений шкалы и нониуса, который называется точностью нониуса, равна
, а разность в длине делений шкалы и нониуса, который называется точностью нониуса, равна 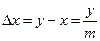 . Эта величина, как мы скоро увидим, и определяет собой максимальную погрешность нониуса.
. Эта величина, как мы скоро увидим, и определяет собой максимальную погрешность нониуса.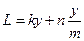
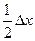 , ибо при большем несовпадении этих делений одно из соседних делений (справа или слева) имело бы несовпадение, меньше чем
, ибо при большем несовпадении этих делений одно из соседних делений (справа или слева) имело бы несовпадение, меньше чем 


