Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции, тела с помощью крестообразного маятника.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ОБОРУДОВАНИЕ: I. Крестообразный маятник с перемещающимися грузами. 2. Вертикальный масштаб. 3. Набор грузов по 50 грамм. 4. Штангенциркуль. 5. Секундомер.
КРАТКАЯ ТЕОРИЯ.
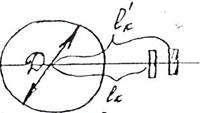
Моментом инерции материальной точки массой m находящейся на расстоянии r от оси вращения, называется произведение масcы этой точки на квадрат расстояния от оси вращения, т.е. Если имеем дело с телом, то моментом инерции его называется сумма моментов инерции всех его точек, т.е. Во вращательном движении момент инерции играет ту же роль, какую в. поступательном движении играет масса. Поэтому определение момента инерции имеет большое практическое значение. Определить момент инерции тела относительно какой-нибудь оси можно путем вычисления, если тело имеет правильную форму и известно распределение массы внутри тела. Но чаще всего приходится определять момент инерции тела относительно какой-нибудь оси опытным путем. В нашей работе для этой цели применяется крестообразный маятник (рис.1). Он представляет собой маховик, с четырьмя взаимно перпендикулярными стержнями, вдоль которых могут перемещаться грузы. Для этих грузов нам и предстоит найти момент инерции. На общей оси маятника находится валик; на валик намотана нить с привязанным грузом. Основное выражение динамики для вращающегося тела выражается так:
где М - момент силы, под влиянием которой тело вращается вокруг оси, I -| момент инерции вращающегося тела,
Из уравнения-(1) имеем:
Таким образом, для определения инерции вращающегося тела нужно знать момент вращающей силы и угловое ускорение тела. Будем искать эти величины.
Привяжем к нити маятника некоторый груз и представим ему возможность падать. Это падение будет равноускоренным. Если высота падения h, а время падения t, то
где а-линейное ускорение. Отсюда: Но с таким ускорением будут двигаться все тела (точки) на поверхности валика. Измерив радиус валика r, можно найти угловое ускорение Е маховика:
Вращающим моментом силы называется произведение силына ее плечо. Напомним, что, плечом называется расстояние от оси вращения до прямой, совпадающей с направлением действия силы. В нашем примере плечо силы равно радиусу валика. Найдем, чему равна сила, вращающая маятник. На груз массы m действуют: I) сила тяжести Р = mg 2) натяжение нити (силы противоположного направления) PH Результирующая сила: F=ma. По второму закону Ньютона, эта сила, действуя на груз массы mбудет перемещать его с ускорением a, т.е.
Отсюда: Но натяжение нити PH численно равно, той силе, которая приводит во вращение крестообразный маятник. Поэтому момент этой силы
Подставив значения М и
ВЫПОЛНЕНИЕ РАБОТЫ. I. Находят момент инерции маятника I1 2.:На стержни маятника на одинаковом расстоянии R от оси вращения, надевают четыре одинаковых груза, каждый массовый момент которого неизвестен и подлежит определению. Затем находят момент инерции всей системы I2. 3. Очевидно, что момент инерции четырех надетых на стержни грузов будет равен 4. Принимая надетые на крестовину грузы за материальные точки, находят их момент инерции I1путем вычисления
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. I. К нити, намотанной на валик, подвесить груз массы m. 2. Нижний обрез груза совместить с верхним делением шкалы. 3. Одновременно отпустить груз и включить секундомер. В тот момент, когда груз ударится о подставку шкалы, выключить секундомер и записать время падения груза. Определение времени t| производится3-5 раз. Определяем tср. 4. Вычислить линейное ускорение груза 5. На стержни маятника надеть четыре груза равной массы m нa одинаковом R расстоянии от оси вращения. 6. Выполнив п.п. 3, вычислить затем по формуле момент инерции всей вращающейся системы
7. Принимая грузы на стержнях за материальные точки, вычислить, их момент инерции по формуле:
где R среднее расстояние груза от оси вращения. 8. Сравнить результаты измерений, полученные по формулам (6) и (7) Данные измерений заносят в таблиц:
m - масса движущегося груза r - радиус валика h- путь, проходимый падающим телом m1- масса исследуемого груза R- расстояние между центром дополнительного груза и осью вращения g - ускорение свободного падения (g=9,8 м/с2);
Рис.2
Контрольные вопросы
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1197; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.006 с.) |

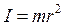
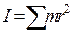 ,
,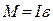 (1)
(1)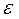 - угловое ускорение тела.
- угловое ускорение тела.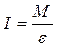 (2)
(2)
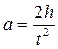
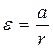 (3)
(3)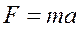
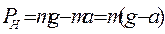
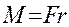
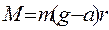 ;
; 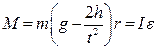 (4)
(4)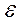 из формул (3) л (4) в формулу (2), получим величину момента инерции вращающегося маятника:
из формул (3) л (4) в формулу (2), получим величину момента инерции вращающегося маятника: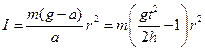 (5)
(5)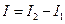
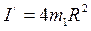 ;
; 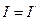
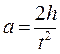 . Затем по формуле (5) вычислить момент инерции маятника (предварительно измерить; радиус валика r).
. Затем по формуле (5) вычислить момент инерции маятника (предварительно измерить; радиус валика r).
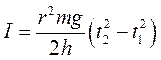 (6)
(6) ; (7)
; (7)
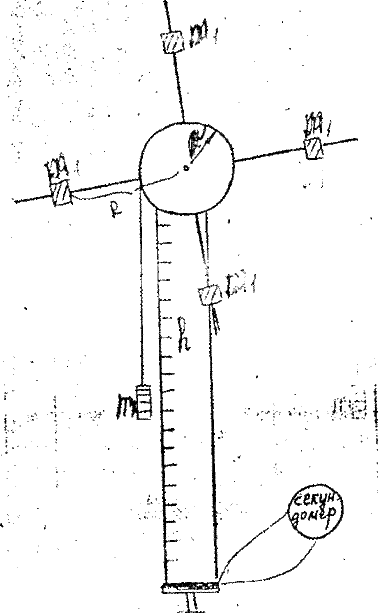 Рис.1
Рис.1