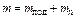Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод формулы для косвенных измерений моментаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тормозящей силы
Для оценки момента тормозящей силы воспользуемся энергетическими соотношениями. Поскольку силы трения являются диссипативными, то работа тормозящей силы А т при переходе системы тело–груз из начального состояния в конечное равна
где Механическая энергия системы складывается из кинетической и потенциальной энергий. В те моменты времени, когда система покоится, кинетическая энергия равна нулю и, следовательно, механическая энергия становится равной только потенциальной энергии системы. Такие состояния системы возникают в начальный момент времени, когда груз находится на отметке
где Будем считать, что момент тормозящей силы в основном связан с вращательным движением тела, т. е. тормозящей силой, действующей на груз, пренебрежем. Тогда элементарная работа момента тормозящей силы равна скалярному произведению
где Оба вектора
Тогда полная работа момента тормозящей силы, если предположить, что он постоянен, равна
где При движении груза вниз от отметки
Очевидно, что при дальнейшем вращении тела до момента, когда груз остановится на отметке
Тогда общий угол поворота тела, соответствующий переходу груза от отметки
Подставляя (4.2) и (4.3) в (4.1), получаем
Отсюда, используя (4.5), получаем формулу для оценки модуля вектора момента тормозящей силы
Вывод формулы для косвенных измерений Момента инерции тела с учетом момента тормозящей силы
Рассмотрим систему тело–груз в начальный момент времени, когда груз находится на отметке Для выбранных начального и конечного состояний получим
где Начальная механическая энергия системы тело–груз равна
Конечная механическая энергия системы складывается из кинетической энергии вращательного движения тела и кинетической энер-
где Строго говоря, в процессе движения груз за счет упругого растяжения нити опускается чуть ниже отметки Предполагая, что движение системы является равноускоренным, для скорости груза на отметке
где Угловая скорость вращения тела в тот же момент времени равна
где Подставляя (4.7) – (4.9) в (4.1), получаем
Из этой формулы, учитывая (4.4), (4.10) и (4.11), выражаем момент инерции
где
Получение формул для определения погрешностей Косвенных измерений момента тормозящей силы И момента инерции тела
Методика получения оценок истинных значений величин и погрешностей при прямых и косвенных измерениях описана в [1]. При выполнении данной лабораторной работы прямыми будут измерения длины Выполнив прямые многократные измерения величин Подставляя в рабочую формулу (4.6) истинные значения всех аргументов, получаем оценку истинного значения момента тормозящей силы
где черта над величиной означает оценку истинного значения. Абсолютная погрешность косвенных измерений величины
С помощью этой формулы, взяв частные производные по всем аргументам, получим
В формулу (4.14) входят пять квадратичных членов, вклад каждого из них в погрешность величины Оценку истинного значения величины момента инерции тела, определяемого в опытах с помощью формулы (4.12), получим, подставив в нее истинные значения входящих аргументов
Абсолютная погрешность косвенных измерений величины
С помощью этой формулы, взяв частные производные по всем аргументам, получим
В формулу (4.16) входит шесть квадратичных членов. Один из них (пятый) связан с погрешностью величины Как было сказано выше, прежде чем применять формулу (4.16), необходимо оценить вклад каждого квадратичного слагаемого, сохранив только наибольшие. Задание к работе 1. Заготовьте таблицу для прямых пятикратных измерений длины 2. Заранее выберите отметку 3. Вращая тело рукой, размотайте нить на полную длину и заранее определите численное значение отметки 4. Включите электронный секундомер. 5. Вращая тело рукой, намотайте нить на шкив так, чтобы груз занял положение, соответствующее выбранной Вами начальной отметке 6. Проведите первый опыт, используя в качестве груза, тянущего нить, только одну подставку массой 7. Пятикратно повторите этот опыт, не меняя массу груза, что необходимо для определения случайной погрешности прямых измерений. 8. Проведите по одному опыту, поместив на подставку сначала один, а затем сразу два подгрузка. Результаты внесите в таблицу измерений. 9. Проведите статистическую обработку пятикратно проведенных прямых измерений величин 10. Проведите оценку истинного значения момента тормозящей силы 11. Проведите численную оценку квадратичных членов формулы (4.14) и, отбросив малые, оцените погрешность косвенных измерений момента тормозящей силы 12. Проведите оценку истинного значения момента инерции тела 13. Проведите численную оценку квадратичных членов формулы (4.16) и, отбросив малые, оцените погрешность косвенных измерений момента инерции тела 14. С помощью формулы (4.6) или (4.13) проведите расчет моментов тормозящей силы для однократных опытов с другими грузами 15. С помощью формулы (4.12) или (4.15) проведите расчет момента инерции тела для однократных опытов с другими грузами (см. п. 8). Погрешности измерений для этих опытов вычислять не надо. Наблюдается ли закономерное изменение момента инерции с ростом массы груза? Контрольные вопросы 1. Какая часть системы совершает в процессе опыта поступательное, а какая – вращательное движение? 2. Почему для описания вращательного движения удобней пользоваться угловыми кинематическими характеристиками, а для поступательного – линейными? 3. Что такое момент силы? Какие силы и моменты сил действуют на тело во время его движения? 4. Какие силы создают момент тормозящей силы? Можно ли указать точку приложения этих сил? 5. Как определить работу момента силы? 6. Сохраняется ли механическая энергия системы тело–груз в процессе опыта? 7. Как можно оценить момент тормозящей силы, пользуясь энергетическими соотношениями? Какие упрощающие предположения при этом делаются? 8. Изменяется ли момент тормозящей силы при увеличении массы груза, как и почему? 9. Что такое момент инерции тела, какое свойство тела он характеризует? 10. Как найти кинетическую энергию при поступательном и при вращательном движении? 11. Как можно определить момент инерции тела, пользуясь энергетическими соотношениями. 12. Зависит ли момент инерции тела от массы груза, закрепленного на конце нити? 13. Выведите формулу кинетической энергии тела, совершающего вращательное движение вокруг неподвижной оси. 14. Выведите рабочую формулу для оценки момента тормозящей силы. 15. Выведите рабочую формулу для момента инерции тела с учетом и без учета момента тормозящей силы. Примените эти формулы, чтобы ответить на вопрос, имеет ли смысл учет момента тормозящей силы в проделанных опытах.
Индивидуальные задания для членов бригады, выполняющих лабораторную работу на одной установке
Литература
1. Введение к настоящим методическим указаниям. 2. Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т. 1
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА МЕТОДОМ КОЛЕБАНИЙ Цель работы – определение момента инерции маятника с применением уравнения колебаний и исследование зависимости момента инерции от расстояния до условно выбранной точки А.
Описание установки
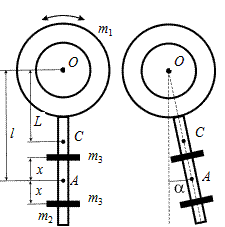
Установка представляет собой физический маятник, т. е. твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр масс. Физический маятник в данной работе состоит из барабана массой m 1 с осью вращения О, стержня массой m 2 и двух грузов с одинаковыми массами m 3, которые можно закрепить в нужном положении на стержне (рис. 5.1).
а б Рис. 5.1
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.153.110 (0.008 с.) |

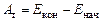 , (4.1)
, (4.1)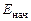 – механическая энергия системы тело–груз в начальном состоянии;
– механическая энергия системы тело–груз в начальном состоянии;  – механическая энергия системы тело–груз в конечном состоянии.
– механическая энергия системы тело–груз в конечном состоянии.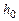 , и в тот момент, когда, опустившись вниз, груз за счет вращения тела поднимается до отметки
, и в тот момент, когда, опустившись вниз, груз за счет вращения тела поднимается до отметки 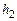 (рис. 4.1). Если принять, что на высоте
(рис. 4.1). Если принять, что на высоте 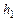 потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно
потенциальная энергия груза равна нулю, то приращение механической энергии для выбранных начального и конечного состояний системы равно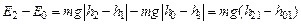 , (4.2)
, (4.2)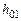 – расстояние между отметками
– расстояние между отметками 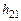 – расстояние между отметками
– расстояние между отметками 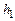 .
.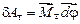 ,
,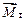 – вектор момента тормозящей силы;
– вектор момента тормозящей силы; 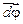 – вектор бесконечно малого углового перемещения тела.
– вектор бесконечно малого углового перемещения тела. .
.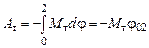 , (4.3)
, (4.3)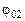 – угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки
– угол поворота тела вокруг оси при переходе системы из начального состояния в конечное (груз при этом перемещается от отметки 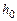 до отметки
до отметки 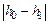 . Учитывая, что длина окружности шкива равна
. Учитывая, что длина окружности шкива равна  и каждый оборот шкива соответствует углу
и каждый оборот шкива соответствует углу 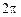 радиан, найдем угол поворота шкива при движении груза вниз
радиан, найдем угол поворота шкива при движении груза вниз [рад]. (4.4)
[рад]. (4.4)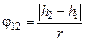 [рад].
[рад].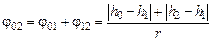 [рад]. (4.5)
[рад]. (4.5)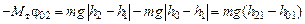 .
.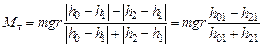 . (4.6)
. (4.6)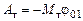 , (4.7)
, (4.7) – момент тормозящей силы (4.6);
– момент тормозящей силы (4.6); 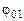 – угол поворота тела, соответствующий перемещению груза от отметки
– угол поворота тела, соответствующий перемещению груза от отметки 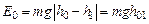 . (4.8)
. (4.8) ,
,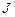 – момент инерции тела;
– момент инерции тела; 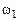 – угловая скорость вращения тела в момент
– угловая скорость вращения тела в момент 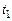 (см. рис. 4.1);
(см. рис. 4.1);  – скорость поступательного движения груза в момент
– скорость поступательного движения груза в момент 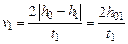 , (4.10)
, (4.10)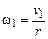 , (4.11)
, (4.11)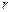 – радиус шкива, на который намотана нить.
– радиус шкива, на который намотана нить. .
.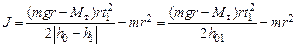 , (4.12)
, (4.12) и времени
и времени 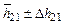 и
и 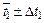 для выбранного значения доверительной вероятности. Эти величины будут в дальнейшем использованы для оценки истинного значения и погрешности при косвенных измерениях.
для выбранного значения доверительной вероятности. Эти величины будут в дальнейшем использованы для оценки истинного значения и погрешности при косвенных измерениях. , (4.13)
, (4.13)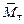 определяется формулой, приведенной в [1]
определяется формулой, приведенной в [1]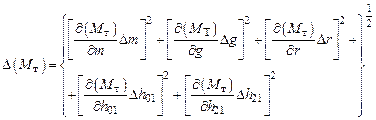 .
.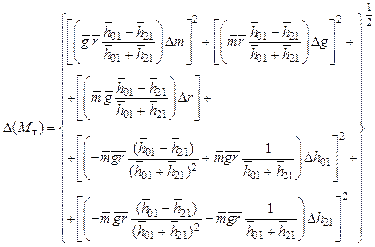 . (4.14)
. (4.14) . (4.15)
. (4.15)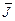 определяется по формуле, приведенной в [1],
определяется по формуле, приведенной в [1],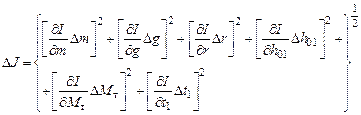 .
.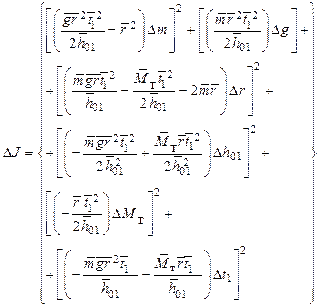 . (4.16)
. (4.16)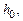 от которой начнется движение груза
от которой начнется движение груза  (рекомендуемое значение 50 см).
(рекомендуемое значение 50 см).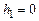 . Внесите длину
. Внесите длину 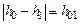 в таблицу. Оцените погрешность измерения этой длины как систематическую погрешность измерительной линейки.
в таблицу. Оцените погрешность измерения этой длины как систематическую погрешность измерительной линейки.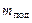 без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №2 (светится индикатор «Реж.2»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее тело, и одновременно включится секундомер. При включенном режиме №2 секундомер в момент прохождения грузом отметки
без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №2 (светится индикатор «Реж.2»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее тело, и одновременно включится секундомер. При включенном режиме №2 секундомер в момент прохождения грузом отметки 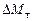 .
.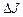 .
.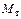 от величины h 2. При расчете считайте величины h 0 и h 1, входящие в формулу, равными
h 0 = 50 см,
от величины h 2. При расчете считайте величины h 0 и h 1, входящие в формулу, равными
h 0 = 50 см, 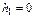 см. Численные значения радиуса шкива возьмите в таблице исходных данных, помещенной в Приложении и около лабораторной установки, на которой Вам предстоит выполнять опыты. Массу m считайте равной
массе подставки
см. Численные значения радиуса шкива возьмите в таблице исходных данных, помещенной в Приложении и около лабораторной установки, на которой Вам предстоит выполнять опыты. Массу m считайте равной
массе подставки  (без подгрузков)
(без подгрузков)