
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный момент и коэффициент корреляции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для характеристики корреляционной зависимости между величинами используются коррекляционный момент и коэффициент корреляции. О п р е д е л е н и е 2. Корреляционным моментом µxy случайных величин X и Y называют математическое ожидание произведения отклонений этих величин
Для вычисления корреляционного момента дискретных величин используется выражение
а для непрерывных – выражение
З а м е ч а н и е. Корреляционный момент µxy может быть переписан в виде
Действительно, используя свойства математического ожидания (см. §§ 2.2; 2.6), имеем
Т е о р е м а. Корреляционный момент двух независимых случайных величин X и Y равен нулю. Д о к а з а т е л ь с т в о. Согласно замечанию
а так как Х и Y независимые случайные величины, то (см. §§ 2.2; 2.6)
и, значит, µxy=0. Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y,т.е. его величина зависит от единиц измерения случайных величин. Поэтому для одних и тех же двух величин величина корреляционного момента может иметь различные значения в зависимости от того, в каких единицах были измерены величины. Для устранения этого недостатка условились за меру связи (зависимости) двух случайных величин X и Yпринять безразмерную величину
где σх=σ(Х), σy=σ(Y), называемую коэффициентом корреляции. П р и м е р 1. Пусть двумерная дискретная случайная величина (X,Y)задана законом распределения:
Найдем корреляционный момент и коэффициент корреляции случайных величин X и Y. Р е ш е н и е. Сложив вероятности по строкам, получим вероятности возможных значений X:
Отсюда закон распределения X:
и, значит, Сложив же вероятности по столбцам, найдем вероятности возможных значений Y:
Отсюда закон распределения Y:
и, значит, Следовательно,
Таким образом, коэффициент корреляции
Т е о р е м а. Абсолютная величина корреляционного момента двух случайных величин не превосходит произведения их средних квадратических отклонений:
Д о к а з а т е л ь с т в о. Введя в рассмотрение случайную величину
(любая дисперсия неотрицательна). Отсюда
Введя случайную величину
В результате имеем
или
О п р е д е л е н и е 2. Случайные величины X и Y называются некоррелированными, если П р и м е р 1. Независимые случайные величины Х и Y являются некоррелированными, так как в силу соотношения (3.12) П р и м е р 2. Пусть случайные величины Х и Y связаны линейной зависимостью
откуда
Поэтому
Таким образом, коэффициент корреляции случайных величин, связанных линейной зависимостью, равен ±1 (точнее, Отметим некоторые свойства коэффициента корреляции. Из примера 1 следует: 1) Если X и Y — независимые случайные величины, то коэффициент корреляции равен нулю. Заметим, что обратное утверждение, вообще говоря, неверно. (Доказательство см. в работе [2].) 2)Абсолютная величина коэффициента корреляции не превосходит единицы:
Действительно, разделив обе части неравенства (3.16) на произведение 3) Как видно из формулы (3.15) с учетом формулы (3.14), коэффициент корреляции характеризует относительную величину отклонения математического ожидания произведения 3. Линейная корреляция. Этот вид корреляционной зависимости встречается довольно часто. О п р е д е л е н и е. Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии Выведем уравнения прямой регрессии Y на X, т.е. найдем коэффициент линейной функции Обозначим М(Х) = а, М(Y) = b, М[(Х - а)2] = М(Y) = М[g(Х)] = М(АХ + В)= АМ(Х) + В, т.е. b = Аа + В, откуда В=b-Аа. Далее, с помощью тех же свойств математического ожидания имеем М(ХY) = М[Хg(Х)\ = М(АХ2 + ВХ) = АМ(Х2) + ВМ(Х) = АМ(Х2) + (b- Аа)а,
откуда А= или, согласно свойству 1 дисперсии (§§ 2.3; 2.6),
Полученный коэффициент называется коэффициентом регрессии Y на X и обозначается через
Таким образом, уравнение прямой регрессии Y на X имеет вид
Аналогично можно получить уравнение прямой регрессии X на Y
где
есть коэффициент регрессии X на Y. Уравнения прямых регрессии можно записать в более симметричном виде, если воспользоваться коэффициентом корреляции. С учетом этого коэффициента имеем:
и поэтому уравнения прямых регрессии принимают вид:
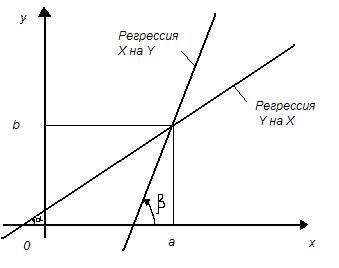
Из уравнений прямых регрессии видно, что обе эти прямые проходят через точку (а;b); угловые коэффициенты прямых регрессии равны соответственно (рис. 13):
рис. 13
Так как При Рис. 13 В этом случае МХ(Y) = b = М(Y); МУ(Х) = а = М(Х). Из формулы (3.21) видно, что коэффициенты регрессии имеют тот же знак, что и коэффициент корреляции
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2800; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.12.188 (0.008 с.) |


 (3.12)
(3.12) (3.13)
(3.13) (3.14)
(3.14)


 (3.15)
(3.15)






 где
где  найдем ее дисперсию. Имеем
найдем ее дисперсию. Имеем

 , аналогично найдем
, аналогично найдем

 (3.16)
(3.16) = 0, и коррелированными, если
= 0, и коррелированными, если 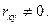
 Найдем коэффициент корреляции. Имеем:
Найдем коэффициент корреляции. Имеем:




 , приходим к искомому неравенству.
, приходим к искомому неравенству. от произведения математических ожиданий М(Х) М(Y) величин X и Y. Так как это отклонение имеет место только для зависимых величин, то можно сказать, что коэффициент корреляции характеризует тесноту зависимости между X и Y.
от произведения математических ожиданий М(Х) М(Y) величин X и Y. Так как это отклонение имеет место только для зависимых величин, то можно сказать, что коэффициент корреляции характеризует тесноту зависимости между X и Y. и
и  являются линейными. В этом случае обе линии регрессии являются прямыми; их называют прямыми регрессии.
являются линейными. В этом случае обе линии регрессии являются прямыми; их называют прямыми регрессии.
 , М[(Y –b2)] =
, М[(Y –b2)] =  . С использованием свойств МО (§§ 2.2; 2.6) находим:
. С использованием свойств МО (§§ 2.2; 2.6) находим:

 :
: (3.17)
(3.17) (3.18)
(3.18) (3.19)
(3.19) (3.20)
(3.20)
 (3.21)
(3.21)


 то
то 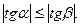 Это означает, что прямая регрессии Y на X имеет меньший наклон к оси абсцисс, чем прямая регрессии X на Y Чем ближе
Это означает, что прямая регрессии Y на X имеет меньший наклон к оси абсцисс, чем прямая регрессии X на Y Чем ближе  к единице, тем меньше угол между прямыми регрессии. Эти прямые сливаются тогда и только тогда, когда
к единице, тем меньше угол между прямыми регрессии. Эти прямые сливаются тогда и только тогда, когда 



