
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный момент св Х и У и его св-ва.Содержание книги
Поиск на нашем сайте
Пусть имеется случайный вектор Корреляционным моментом
1. 2. Если Обратное, вообще говоря, не имеет места. Если 3.
Если отклонения случайных величин заменить их нормированными отклонениями, то получим безмерную величину - коэффициент линейной корреляции
29.Формула Бернулли Пусть некоторый опыт воспроизводится
Найдем вероятность отдельного случая. Чтобы он наступил, должны наступить события
где Мы видим, что все частные случаи равновозможны, поэтому, применяя теорему сложения для несовместных событий, получаем
30.Наивероятнейшим числом наступления события Число наступлений события Пусть Итак, 31. Асимптотические формулы вычисления вероятностей При больших Теорема. Если вероятность
где При сделанных предположениях относительно
Формула Теорема. Пусть проводится
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.76 (0.007 с.) |

 , распределение которого известно, т. е. известна таблица или плотность распределения
, распределение которого известно, т. е. известна таблица или плотность распределения  . Тогда
. Тогда  ,
, 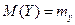 . По известному закону распределения можно найти также дисперсии составляющих вектор
. По известному закону распределения можно найти также дисперсии составляющих вектор 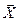 . Пусть
. Пусть  и
и  . Однако математические ожидания и дисперсии случайных величин
. Однако математические ожидания и дисперсии случайных величин  и
и  недостаточно полно характеризуют случайный вектор
недостаточно полно характеризуют случайный вектор  случайных величин
случайных величин  . Если распределение дискретное, то
. Если распределение дискретное, то  . При непрерывном распределении
. При непрерывном распределении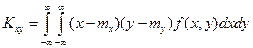 . Корреляционный момент обладает след-ми св-вами:
. Корреляционный момент обладает след-ми св-вами: –симметричность.
–симметричность. независимые св, то
независимые св, то 
 , то в этом случае величины
, то в этом случае величины  . Действительно,
. Действительно,  ;
;

 :
: Свойства коэффициента линейной корреляции вытекают из свойств корреляционного момента:
Свойства коэффициента линейной корреляции вытекают из свойств корреляционного момента:  ; 2.
; 2.  ; 3.
; 3. 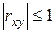 ; 4и5
; 4и5 раз и каждый раз событие
раз и каждый раз событие  может наступать с одной и той же вероятностью
может наступать с одной и той же вероятностью  , независимо от результатов предыдущих опытов. В этом случае говорят о повторных независимых испытаниях. При этом событие
, независимо от результатов предыдущих опытов. В этом случае говорят о повторных независимых испытаниях. При этом событие  , …,
, …,  . Интересующее нас событие – наступление
. Интересующее нас событие – наступление  - это наступление
- это наступление  -ом испытании. Набор таких
-ом испытании. Набор таких  ,
,  ,…,
,…, 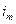 )- это случай, когда
)- это случай, когда  (1,2,3,…,
(1,2,3,…, 
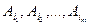 и события
и события  , где
, где  пробегает те числа из 1,2,3,…,
пробегает те числа из 1,2,3,…, 




 .
. - формула Бернулли.
- формула Бернулли. - наивероятнейшее число наступлений события
- наивероятнейшее число наступлений события  ,
,  . Отсюда
. Отсюда  или
или  , следовательно,
, следовательно,  . С другой стороны,
. С другой стороны,  , тогда
, тогда  , т.е.
, т.е.  .
.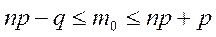 . Отметим, что разность
. Отметим, что разность  , следовательно, всегда существует целое число
, следовательно, всегда существует целое число  - целое число, то наивероятнейших чисел будет два:
- целое число, то наивероятнейших чисел будет два:  и
и  .
.
 и
и  на практике пользоваться формулой Бернулли
на практике пользоваться формулой Бернулли  затруднительно.В этом случае пользуютсялокальной теоремой Лапласа, которую приведем без доказательства.
затруднительно.В этом случае пользуютсялокальной теоремой Лапласа, которую приведем без доказательства. -вероятность того, чтособытие
-вероятность того, чтособытие  удовлетворяет предельному неравенству
удовлетворяет предельному неравенству ,
,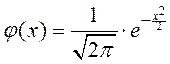 ,
,  .
. .
. эффективнее, когда
эффективнее, когда  , причем
, причем  - величина постоянная, то
- величина постоянная, то .
.


