
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия из теоремы умножения вероятностейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Следствие 1. Если событие Доказательство. Дано, что Требуется доказать, что и событие При доказательстве предполагаем, что
или принимая во внимание выше Из этого следствия вытекает, что зависимость и независимость событий всегда взаимны. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных. Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий. Это следствие непосредственно вытекает из определения независимых событий. Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий. В общем виде она формулируется так: Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:
Доказательство проводится методом полной индукции. В случае независимых событий теорема упрощается и принимает вид:
т. е. вероятность произведения независимых событий равна произведению вероятностей этих событий или
Формула полной вероятности Следствием обеих теорем - теоремы сложения и умножения - является так называемая формула полной вероятности. Пусть требуется определить вероятность некоторого события Докажем, что в этом случае
т. е. вероятность события Формула (*) носит название формулы полной вероятности. Доказательство. Так как гипотезы
Т. к. гипотезы
Применяя к событию
что и требовалось доказать. Пример. На фабрике, изготовляющей болты, первая машина производит 30%, вторая- 25%, третья- 45% всех изделий. Брак в их продукции составляет соответственно 2%, 1% и 3%. Найти вероятность того, что случайно выбранный болт оказался дефектным. Решение. Обозначим через 12. Теорема гипотез. (Формула Байеса) Следствием теоремы умножения и формулы полной вероятности является так называемая гипотез, или формула Байеса. Поставим следующую задачу. Имеется полная группа несовместных гипотез Здесь, по существу, речь идет о том, чтобы найти условную вероятность Из теоремы умножения имеем:
или, отбрасывая левую часть, откуда
Выражая Р(А) с помощью формулы полной вероятности, имеем
Пример. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго - 0,4. После стрельбы по мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку. Решение. До опыта возможны следующие гипотезы:
Условные вероятности наблюденного события
После опыта невозможные гипотезы ¾
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.18.135 (0.01 с.) |

 не зависит от события
не зависит от события  , то и событие
, то и событие  (**)
(**)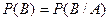 (**)
(**) . Напишем теорему вероятностей в двух формах:
. Напишем теорему вероятностей в двух формах:
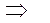


 . Разделим обе части на
. Разделим обе части на  . Тогда
. Тогда 
 .
.
 ,
, .
. , образующих полную группу несовместных событий. Будем называть эти события гипотезами.
, образующих полную группу несовместных событий. Будем называть эти события гипотезами.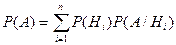 , (*)
, (*) .
. - также несовместны. Покажем это -
- также несовместны. Покажем это -  . Применяя к ним теорему сложения, получим
. Применяя к ним теорему сложения, получим .
. теорему умножения, получим
теорему умножения, получим – события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что
– события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что 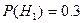 ,
,  ,
,  ;
;  ,
, 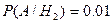 ,
, 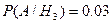 . По формуле полной вероятности получаем, что
. По формуле полной вероятности получаем, что  . Произведен опыт, в результате которого наблюдено появление некоторого события
. Произведен опыт, в результате которого наблюдено появление некоторого события  для каждой гипотезы.
для каждой гипотезы.

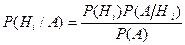 ,
, 
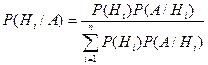 ,
, 
 - ни первый, ни второй не попадут;
- ни первый, ни второй не попадут;  - оба попадут;
- оба попадут;  - первый попадет, второй - нет;
- первый попадет, второй - нет;  - первый не попадет, второй попадет. Вероятность этих гипотез:
- первый не попадет, второй попадет. Вероятность этих гипотез: =0,2×0,6=0,12;
=0,2×0,6=0,12;  =0,32;
=0,32; 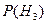 =0,8×0,6=0,48;
=0,8×0,6=0,48;  =0,2×0,4=0,08.
=0,2×0,4=0,08.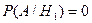 ;
; 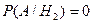 ;
;  ;
;  .
. .
. 


