
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы сложения и умножения вероятностей для совместных и не совместных событий.Содержание книги
Поиск на нашем сайте
Умножения: Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило: Доказательство. Докажем теорему для случая, когда опыт имеет конечное число несовместных равновероятных исходов. Пусть: · событие · событие · событие Вероятность события или Следствие 1. Обобщим теорему на случай трех событий: Следствие 2. Обобщим теорему на случай Сложения: Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Формула полной вероятности и формула байесса Если событие А может произойти только при выполнении одного из событий
Эта формула называется формулой полной вероятности. Вновь рассмотрим полную группу несовместных событий
Если событие А произошло, то это может изменить вероятности гипотез По теореме умножения вероятностей
откуда
Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса). Основные понятия и формулы комбинаторики.
комбинаторика, - раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Комбинаторика - один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике.
Формула размещения - выборки которые различаются как по составу, так и по расположению элементов.
Формула перестановки - выборки, различающиеся только по расположению элементов. Pn = n! Формула сочетания - выборки, которые различаются только по составу (из всей совокупности часть, порядок НЕ важен)
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.25.216 (0.005 с.) |


 появилось в
появилось в  исходах опыта;
исходах опыта; появилось в
появилось в  исходах опыта;
исходах опыта; появилось в
появилось в  исходах опыта.
исходах опыта. вычислим по классическому определению. Поскольку событие
вычислим по классическому определению. Поскольку событие 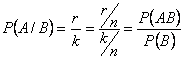 ,
, .
.
 событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились:
событий: в случае произведения нескольких зависимых событий вероятность равна произведению одного из них на условные вероятности всех остальных при условии, что вероятность каждого последующего вычисляется в предположении, что все остальные события уже совершились: .
. .
. .
.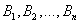 , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле .
. . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий  ,
, .
.





