
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение некоторых функций в ряд МаклоренаСодержание книги
Поиск на нашем сайте
МАТЕМАТИКА (29-56) 29. Основные понятия теории числовых рядов. Числовой ряд – это сумма членов числовой последовательности вида:
ak - называют общим членом числового ряда или k–ым членом ряда. В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: Числовой ряд Суммой сходящегося числового ряда Еще одним примером расходящегося числового ряда является сумма вида В этом случае n–ая частичная сумма может быть вычислена как Сумма вида
30. Свойства положительных числовых рядов. Необходимый признак сходимости. Теорема. Если ряд сходится, то предел его общего члена при
равен нулю, т.е.
Следствие. Если предел общего члена ряда при
не равен нулю, то ряд расходится. Пусть дан ряд Признак Коши. Пусть существует если если если Признак Даламбера. Пусть существует если если если 31. Сходимость положительных числовых рядов:признаки сравнения. Признак сравнения: Теорема (признак сравнения). Пусть даны два ряда с положительными членами
причём члены первого ряда не превосходят соответствующих членов второго, т.е.
Тогда из сходимости второго ряда следует сходимость первого, а из расходимости первого ряда – расходимость второго.
32. Сходимость положительных числовых рядов: радикальный признак Коши, признак Д’аламбера, интегральный признак Коши. Интегральный признак Коши: Пусть f (x) – некоторая функция, определенная на интервале [1, ¥). В этом разделе рассматриваются ряды вида Интегральный признак Коши. Пусть при x ®¥ функция f (x) монотонно убывает до нуля, то есть
Признак Д’аламбера: Признак Даламбера. Пусть существует если если если Радикальный признак Коши: Радикальный признак Коши — признак сходимости числового ряда: Если для числового ряда
с неотрицательными членами существует такое число 33. Сходимость знакопеременных и знакочередующихся числовых рядов. Признак лейбница. Абсолютная и условная сходимость. Числовой ряд называется знакоположительным, если un >0 при всех n =1,2,3…. Если первый член знакочередующегося ряда положителен, то этот ряд можно записать в виде
а если отрицателен – виде
Признак Лейбница. Если при Для этого случая имеет место следующая оценка остатка ряда Абсолютная сходимость. Для знакопеременного ряда существует понятие абсолютной и условной сходимости. Знакопеременный ряд
Условная сходимость. Знакопеременный ряд 34. Функциональные ряды. Основные понятия. Формально записанное выражение
где При различных значениях Для определения области сходимости функциональных рядов обычно вначале используется признак Даламбера, а затем те значения 35. Степенные ряды. Теорема Абеля. Среди функциональных рядов наиболее важное место занимают степенные ряды. Степенным рядом называют ряд
члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x, а
теорема Абеля Если степенной ряд сходится при некотором значении Следствие. Если степенной ряд расходится при некотором значении 36. Определение радиуса и области сходимости степенных рядов. Интервал (-R,R), где число R называется интервалом сходимости ряда, а число R – радиусом сходимости этого ряда радиус сходимости степенного ряда определяют с помощью признака сходимости Даламбера. Предположим, что все коэффициенты ряда отличны от нуля и существует предел Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится. Для нахождения области сходимости степенного ряда важную роль играет теорема абеля. теорема Абеля Если степенной ряд сходится при некотором значении 37. Ряды тейлора и Маклорена. Разложение функизй на ряды Тейлора и Маклорена. Ряд Тейлора — разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора. Пусть функция f (x) бесконечно дифференцируема в некоторой окрестности точки a, тогда ряд
В случае, если a = 0, этот ряд иногда называется рядом Маклорена. Если a = 0, то такое разложение называется рядом Маклорена:
Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a. Основные понятия и формулы комбинаторики. комбинаторика, - раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Комбинаторика - один из разделов дискретной математики, который приобрел важное значение в связи с использованием его в теории вероятностей, математической логике, теории чисел, вычислительной технике, кибернетике.
Формула размещения - выборки которые различаются как по составу, так и по расположению элементов.
Формула перестановки - выборки, различающиеся только по расположению элементов. Pn = n! Формула сочетания - выборки, которые различаются только по составу (из всей совокупности часть, порядок НЕ важен)
П П 49. МАТЕМАТИКА (29-56) 29. Основные понятия теории числовых рядов. Числовой ряд – это сумма членов числовой последовательности вида:
ak - называют общим членом числового ряда или k–ым членом ряда. В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: Числовой ряд Суммой сходящегося числового ряда Еще одним примером расходящегося числового ряда является сумма вида В этом случае n–ая частичная сумма может быть вычислена как Сумма вида
30. Свойства положительных числовых рядов. Необходимый признак сходимости. Теорема. Если ряд сходится, то предел его общего члена при
равен нулю, т.е.
Следствие. Если предел общего члена ряда при
не равен нулю, то ряд расходится. Пусть дан ряд Признак Коши. Пусть существует если если если Признак Даламбера. Пусть существует если если если 31. Сходимость положительных числовых рядов:признаки сравнения. Признак сравнения: Теорема (признак сравнения). Пусть даны два ряда с положительными членами
причём члены первого ряда не превосходят соответствующих членов второго, т.е.
Тогда из сходимости второго ряда следует сходимость первого, а из расходимости первого ряда – расходимость второго.
32. Сходимость положительных числовых рядов: радикальный признак Коши, признак Д’аламбера, интегральный признак Коши. Интегральный признак Коши: Пусть f (x) – некоторая функция, определенная на интервале [1, ¥). В этом разделе рассматриваются ряды вида Интегральный признак Коши. Пусть при x ®¥ функция f (x) монотонно убывает до нуля, то есть
Признак Д’аламбера: Признак Даламбера. Пусть существует если если если Радикальный признак Коши: Радикальный признак Коши — признак сходимости числового ряда: Если для числового ряда
с неотрицательными членами существует такое число 33. Сходимость знакопеременных и знакочередующихся числовых рядов. Признак лейбница. Абсолютная и условная сходимость. Числовой ряд называется знакоположительным, если un >0 при всех n =1,2,3…. Если первый член знакочередующегося ряда положителен, то этот ряд можно записать в виде
а если отрицателен – виде
Признак Лейбница. Если при Для этого случая имеет место следующая оценка остатка ряда Абсолютная сходимость. Для знакопеременного ряда существует понятие абсолютной и условной сходимости. Знакопеременный ряд
Условная сходимость. Знакопеременный ряд 34. Функциональные ряды. Основные понятия. Формально записанное выражение
где При различных значениях Для определения области сходимости функциональных рядов обычно вначале используется признак Даламбера, а затем те значения 35. Степенные ряды. Теорема Абеля. Среди функциональных рядов наиболее важное место занимают степенные ряды. Степенным рядом называют ряд
члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x, а
теорема Абеля Если степенной ряд сходится при некотором значении Следствие. Если степенной ряд расходится при некотором значении 36. Определение радиуса и области сходимости степенных рядов. Интервал (-R,R), где число R называется интервалом сходимости ряда, а число R – радиусом сходимости этого ряда радиус сходимости степенного ряда определяют с помощью признака сходимости Даламбера. Предположим, что все коэффициенты ряда отличны от нуля и существует предел Областью сходимости степенного ряда называется множество тех значений х, при которых степенной ряд сходится. Для нахождения области сходимости степенного ряда важную роль играет теорема абеля. теорема Абеля Если степенной ряд сходится при некотором значении 37. Ряды тейлора и Маклорена. Разложение функизй на ряды Тейлора и Маклорена. Ряд Тейлора — разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора. Пусть функция f (x) бесконечно дифференцируема в некоторой окрестности точки a, тогда ряд
В случае, если a = 0, этот ряд иногда называется рядом Маклорена. Если a = 0, то такое разложение называется рядом Маклорена:
Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a. Разложение некоторых функций в ряд Маклорена · · · · · 38. Случайное событие и основные понятия свзязаные с ним. Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом
частотой появления события A в данной серии испытаний P*(A)=m/n. m число наступлений данного случайного события A в данной серии испытаний n число испытаний этой серии называется частотой появления события A в данной серии испытаний вероятность число, около которого колеблется наблюдаемая частота события.
39. Определение вероятности: аксиоматическое классическое статическое геометрическое. Вероя́тность — численная мера возможности наступления некоторого события.
Классическое опр: Вероятностью
Аксиоматическое опр: Пусть задано пространство элементарных событий Е и каждому событию А
Тогда говорят, что на событиях в множестве Е задана вероятность, а число Р (А) называется вероятностью события А. Статическое опр: где m - число испытаний, в которых событие A наступило, n - общее число произведённых испытаний.
Относительная частота события обладает свойством устойчивости: lim n →∞ P (∣ ∣ nm − p ∣ ∣ <ε)=1 (свойство устойчивости относительной частоты) Геометрическое опр: Пусть некоторая n-мерная фигура (отрезок, плоская фигура, пространственная фигура) составляет часть другой n-мерной фигуры. Если предположить, что вероятность попадания точки на эту фигуру пропорциональна её мере (длине, площади, объёму) и не зависит от взаимного расположения меньшей и большей фигур, то вероятность попадания точки на эту фигуру определяется равенствами
где l(L), s(S), v(V) - длина, площадь и объём меньшей и большей n-мерных фигур соответственно. 40. Свойства вероятности. Свойство 1. Если можно вычислить возможности возникновения события А и их число совпадает общим числом равновозможных событий, то вероятность события А равна 1. Например, при бросании игральной кости число возможностей выпадения чисел 1, 2, 3, 4, 5, 6 равно 6. Насчитывается также 6 равновозможных несовместимых событий. Таким образом, M = N и
Свойство 2. Вероятность невозможного события равна 0. Если число возможностей события А равна 0, то и
Например, при бросании игральной кости не может выпасть число 9, потому что такого числа нет на гранях игральной кости. Свойство 3. Вероятность случайного события всегда больше 0 и меньше 1:
или
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.170.253 (0.01 с.) |


 .
. называется сходящимся, если существует конечный предел последовательности частичных сумм
называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд  .
.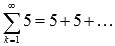 .
. . Предел частичных сумм бесконечен
. Предел частичных сумм бесконечен  .
. называется гармоническим числовым рядом.
называется гармоническим числовым рядом.

 все слагаемые которого положительны
все слагаемые которого положительны  .
. . Тогда
. Тогда , то ряд
, то ряд  , то ряд
, то ряд 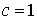 , то о сходимости или расходимости ряда ничего сказать нельзя.
, то о сходимости или расходимости ряда ничего сказать нельзя. . Тогда
. Тогда , то ряд
, то ряд 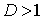 , то ряд
, то ряд  , то о сходимости или расходимости ряда ничего сказать нельзя.
, то о сходимости или расходимости ряда ничего сказать нельзя.

 , то есть ряды со слагаемыми вида
, то есть ряды со слагаемыми вида  .
. . Тогда ряд
. Тогда ряд  сходится или расходится одновременно с интегралом
сходится или расходится одновременно с интегралом  .
.
 ,
,  , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство 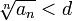 , то данный ряд сходится.
, то данный ряд сходится.

 , то ряд
, то ряд  сходится.
сходится. ,то есть остаток ряда меньше первого отброшенного слагаемого.
,то есть остаток ряда меньше первого отброшенного слагаемого.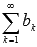 называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд
называется абсолютно сходящимся, если сходится ряд из абсолютных величин его членов, то есть, сходится знакоположительный числовой ряд  .
.
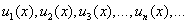 - последовательность функций от независимой переменной x, называется функциональным рядом.
- последовательность функций от независимой переменной x, называется функциональным рядом. из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.
 - постоянные величины. Числа
- постоянные величины. Числа  - коэффициенты членов ряда,
- коэффициенты членов ряда,  - свободный член. Члены степенного ряда определены на всей числовой прямой.
- свободный член. Члены степенного ряда определены на всей числовой прямой.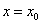 , отличном от нуля, то он сходится, и притом абсолютно, при всех значениях
, отличном от нуля, то он сходится, и притом абсолютно, при всех значениях  .
.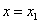 , то он расходится и при всех значениях
, то он расходится и при всех значениях  .
. Тогда радиус сходимости находится по формуле
Тогда радиус сходимости находится по формуле 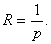 .
. называется рядом Тейлора функции f в точке a.
называется рядом Тейлора функции f в точке a.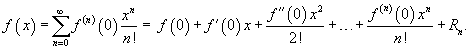







 . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом
. Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом  .
. события
события  называется число, равное отношению числа элементарных исходов, составляющих событие
называется число, равное отношению числа элементарных исходов, составляющих событие 
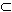 Е поставлено в соответствие единственное число Р (А) такое, что:
Е поставлено в соответствие единственное число Р (А) такое, что:










