
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия нормального закона распределения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Найдем дисперсию
Таким образом, Мы установили вероятностный смысл параметров Функция Лапласа и ее связь с функцией распределе- ния нормальной случайной величины Функция 1) область определения функции Лапласа – вся числовая ось; 2) функция Лапласа монотонно возрастает на всей числовой прямой, т.к. 3) функция
4) Итак, пусть у нас имеется нормальная случайная величина X с математическим ожиданием а и дисперсией
Если Найдем вероятность того, что случайная величина
Таким образом,
Найдем вероятность того, что отклонение нормальной случайной величины от ее математического ожидания по модулю меньше некоторого положительного
Итак: Вероятность того, что нормальная случайная величина отклоняется от своего математического ожидания по модулю меньше, чем на Правило 3 сигм Найдем вероятность того, что отклонение нормальной случайной величины от ее математического ожидания по модулю меньше некоторого положительного
Итак:
Вероятность того, что нормальная случайная величина отклоняется от своего математического ожидания по модулю меньше, чем на
Если в этой формуле положить
Отсюда вытекает, что среди 10000 значений нормальной случайной величины в среднем только 27 выйдут за пределы интервала
41. Неравенство Маркова Теорема. Если случайная величина
Доказательство. Пусть Математическое ожидание случайной величины
Так как
Итак,
Если это неравенство вычесть из тождества 1=1, то
42. Неравенство Чебышева Теорема. Каково бы ни было
Доказательство. Рассмотрим величину
Для
Подставим в это неравенство выражение
Определение. Последовательность чисел Теорема Чебышева Если
Доказательство. Последовательность
Здесь мы воспользовались свойством, что если случайные величины независимы, то дисперсия их суммы равна сумме их дисперсий. Таким образом, Итак, Пусть Отсюда Теорема Бернулли Пусть комплекс условий S воспроизводится n раз, и каждый раз событие А может происходить с одной и той же вероятностью р независимо от результатов предыдущих опытов. Тогда вероятность того, что отклолнение частоты от вероятности р< по модулю положительного числа
Доказательство: Пусть случайная величина
Найдем числовые характеристики этого распределения Отсюда видно, что все требования т. Чебышева выполняется, а значит, если сумму Устремляя Теорема Ляпунова Можно доказать, что CBX1X2…Xn –являются независим нормально распределенными CB, то сумма также распределена по номмальному закону с мат. Ожиданием равным сумме мат. ожиданий и дисперсией равной сумме дисперсий. Обобщением этого утверждения является следующая Т. Ляпунова Т. Если X1X2…Xn –независимые CB, у каждой из которых существует мат ожидание и диспепсия
Следствием из Т. Липунова являются следующие неравенства: 1) 2) 3)
Здесь γ и ε –любые положительные числа, а также a1=a2=…=an=a, Например, если производятся измерения некоторой величины, истинное значение которой равно a, то среднее арифметическое значение результатов измерений отличается от истинного значения по модулю меньше чем ε с вероятностью прибл равной
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 4709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.7.179 (0.01 с.) |


 ,
,  ,
, 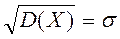 .
. и а, а - это математическое ожидание распределения,
и а, а - это математическое ожидание распределения,  называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства:
называется функцией Лапласа или интегралом вероятности. Она тесно связана с нормальным законом распределения. Ее основные свойства: ;
;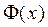 - нечетная, покажем это.
- нечетная, покажем это.
 . Действительно,
. Действительно, 
 . Тогда функция распределения этой случайной величины
. Тогда функция распределения этой случайной величины . Сделаем замену переменной в этом интеграле, положив
. Сделаем замену переменной в этом интеграле, положив  . Тогда
. Тогда  , при
, при  ,
,  , при
, при 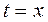 ,
, 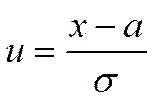 .
.
 , то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием
, то случайная величина называется нормированной. График функции распределения нормированной нормальной случайной величины с математическим ожиданием  , т.е.
, т.е.  имеет вид:
имеет вид: , распределенная по нормальному закону с параметрами
, распределенная по нормальному закону с параметрами  ,
, 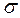 , примет значение из
, примет значение из 

 .
. , т.е. найдем вероятность
, т.е. найдем вероятность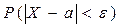 .
.
 .
. , определяется формулой
, определяется формулой  .
. .
.
 .
. .
. , то получим
, то получим .
.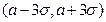 . Это означает, что практически среди небольшого числа значений
. Это означает, что практически среди небольшого числа значений  нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике.
нет таких, которые выходят за пределы указанного интервала. В этом и состоит правило «трех сигм», которое широко применяется в статистике. может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина
может принимать только неотрицательные значения и у нее есть математическое ожидание, то какова бы ни была величина  той же размерности, что и
той же размерности, что и  , всегда выполняется неравенство
, всегда выполняется неравенство .
. . Из условия теоремы следует, что
. Из условия теоремы следует, что  при
при  и
и  при
при  .
. -
- (разобьем на два интеграла)
(разобьем на два интеграла) .
.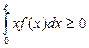 , то
, то .
. ,
,  .
. или
или  . Что и требовалось доказать.
. Что и требовалось доказать. для любой случайной величины
для любой случайной величины  .
. .
. .
. получим
получим .
. через
через 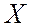 и
и 
 или
или
 называется равномерно ограниченной, если существует такая постоянная М, что для любого
называется равномерно ограниченной, если существует такая постоянная М, что для любого 
 - последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание
- последовательность попарно независимых случайных величин, у каждой из которых есть математическое ожидание  и дисперсия
и дисперсия  ,
,  , причем дисперсии равномерно ограничены, то для любого положительного
, причем дисперсии равномерно ограничены, то для любого положительного 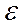

 равномерно ограничена, т.е. существует такое М, что для любого натурального
равномерно ограничена, т.е. существует такое М, что для любого натурального  . Рассмотрим случайную величину
. Рассмотрим случайную величину . У этой величины есть математическое ожидание и дисперсия:
. У этой величины есть математическое ожидание и дисперсия: ,
,
 удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом
удовлетворяет всем требованиям для применения неравенства Чебышева, а значит, при любом  имеем
имеем  или
или 

 , тогда
, тогда  при любых
при любых  .
. , что и требовалось доказать.
, что и требовалось доказать. , стремится к достоверной, при
, стремится к достоверной, при  , т.е.
, т.е.  .
. - число наступлений события А в i -ом испытании, тогда распределение этой случайной величины задается таблицей:
- число наступлений события А в i -ом испытании, тогда распределение этой случайной величины задается таблицей:


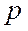
 ,
,  .
.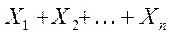 обозначить через m (это число наступлений события А в n испытаниях)
обозначить через m (это число наступлений события А в n испытаниях)

 ,
,  ,
,  также существует
также существует  , а также
, а также , тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для
, тогда сумма S=X1+X2+…+Xn распределена асимптотически по нормальному закону с мат ожид равным сумме мат ожид и дисперсий равной сумме дисперсий, тогда для 
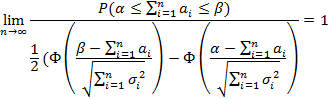
 – ранее вывели. Ф-ция Лапласа.
– ранее вывели. Ф-ция Лапласа.







