
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одномодове волокно з зміщеною ненульовою дисперсією nzsdfСодержание книги
Поиск на нашем сайте
На відміну від DSF-волокна це волокно оптимізоване для декількох довжин хвиль. Такі волокна виготовляють шляхом створення депресивного кільця в оптичній оболонці. Ці волокна називають ще одномодовими волокнами з згладженою (вирівняною) дисперсією. Дисперсія таких волокон приблизно та сама, як і у стандартного волокна з ступінчастим профілем для довжини хвилі 1.31 мкм. Проте з збільшенням довжини хвилі хвости хвиль проникають у депресивне кільце із більшим показником заломлення. Відповідно збільшується загальна швидкість розповсюдження хвилі вздовж хвилеводу. При цьому відомо, що для більшої довжини хвилі показник заломлення середовища менший ніж для хвиль з меншою довжиною. Це явище, як відомо, має назву звичайної дисперсії або “матеріальної” дисперсії. Отже, “хвильова” дисперсія (проникнення хвилі в шар світловоду з більш високим показником заломлення) компенсує “матеріальну” дисперсію. Внаслідок цього константи розповсюдження всіх коливань з різною довжиною хвилі залишаються приблизно однаковими, тобто створюється можливість передавати сигнали з декількома довжинами хвиль (мультиплексний хвильовий сигнал).
Дисперсія
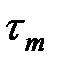 здебільшого вимірюється в пс/км (час затримки на одиницю довжини). Хроматична дисперсія здебільшого вимірюється в пс/км (час затримки на одиницю довжини). Хроматична дисперсія  характеризується коефіцієнтом дисперсії що вимірюється в пс/(нм км). Поведінка коефіцієнту хроматичної дисперсії подана на рисунку 1.3.3. характеризується коефіцієнтом дисперсії що вимірюється в пс/(нм км). Поведінка коефіцієнту хроматичної дисперсії подана на рисунку 1.3.3.
Повна дисперсія у волокні визначається за виразом:
де Як бачимо з рисунка для волокон з складним профілем показника заломлення може спостерігатися декілька точок нульової дисперсії
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.123.194 (0.006 с.) |

 Ще раз повернемося до явища дисперсії та підсумуємо відомі факти (див. частину І посібника, п. 2.4). Дисперсія поділяється на міжмодову (модову) та хроматичну. Хроматичну дисперсію у свою чергу можна поділити на матеріальну (звичайну) дисперсію та хвильову, яка має місце градієнтних волокнах. У нашому розгляді випущено ще один тип дисперсії - так звану поляризаційну дисперсію. Такого типу дисперсія може виникати, наприклад, у волокнах, в яких спостерігаються відхилення форми перерізу волокна від кола. Оптична хвиля, як відомо, має векторний характер, тобто процес розповсюдження хвилі у волокні можна представити як розповсюдження ТЕ- і ТМ-коливання. Якщо структура волокна однорідна, переріз правильної форми, то ТЕ- і ТМ-хвилі мають однакові константи розповсюдження. Проте в процесі виготовлення або прокладки волокна коло може перетворитися на еліпс. Окрім цього, за рахунок вигинів, інших механічних збурень може виникати локальна анізотропія. У такому випадку ТЕ- і ТМ-моди мають різні константи розповсюдження. Отже, процес розповсюдження інформаційного сигналу супроводжується руйнуванням сигналу внаслідок різної швидкості, яка притаманна ортогонально-поляризованим модам. Зауважимо що, поляризаційна дисперсія за порядком набагато менше ніж міжмодова та хроматична. Отже, такою дисперсією можна нехтувати (особливо для багатомодових волокон). Проте у випадку, коли модова та хроматична дисперсії практично скомпенсовані та на граничних за довжиною ділянках ліній (особливо для одномодових волокон) вплив поляризаційної дисперсії стає досить помітним.
Ще раз повернемося до явища дисперсії та підсумуємо відомі факти (див. частину І посібника, п. 2.4). Дисперсія поділяється на міжмодову (модову) та хроматичну. Хроматичну дисперсію у свою чергу можна поділити на матеріальну (звичайну) дисперсію та хвильову, яка має місце градієнтних волокнах. У нашому розгляді випущено ще один тип дисперсії - так звану поляризаційну дисперсію. Такого типу дисперсія може виникати, наприклад, у волокнах, в яких спостерігаються відхилення форми перерізу волокна від кола. Оптична хвиля, як відомо, має векторний характер, тобто процес розповсюдження хвилі у волокні можна представити як розповсюдження ТЕ- і ТМ-коливання. Якщо структура волокна однорідна, переріз правильної форми, то ТЕ- і ТМ-хвилі мають однакові константи розповсюдження. Проте в процесі виготовлення або прокладки волокна коло може перетворитися на еліпс. Окрім цього, за рахунок вигинів, інших механічних збурень може виникати локальна анізотропія. У такому випадку ТЕ- і ТМ-моди мають різні константи розповсюдження. Отже, процес розповсюдження інформаційного сигналу супроводжується руйнуванням сигналу внаслідок різної швидкості, яка притаманна ортогонально-поляризованим модам. Зауважимо що, поляризаційна дисперсія за порядком набагато менше ніж міжмодова та хроматична. Отже, такою дисперсією можна нехтувати (особливо для багатомодових волокон). Проте у випадку, коли модова та хроматична дисперсії практично скомпенсовані та на граничних за довжиною ділянках ліній (особливо для одномодових волокон) вплив поляризаційної дисперсії стає досить помітним.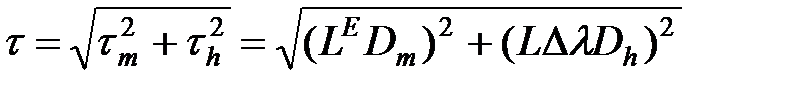 , (1.3.2)
, (1.3.2) – коефіцієнт міжмодової дисперсії,
– коефіцієнт міжмодової дисперсії,  – коефіцієнт хроматичної дисперсії,
– коефіцієнт хроматичної дисперсії,  – ширина спектральної лінії,
– ширина спектральної лінії, 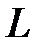 – довжина волокна,
– довжина волокна,  – коефіцієнт зв’язку мод, який являє собою емпіричну величину зі значенням 0.6-0.7. Вираз (1.3.2) справедливий, якщо нехтувати поляризаційною дисперсією. Коефіцієнт
– коефіцієнт зв’язку мод, який являє собою емпіричну величину зі значенням 0.6-0.7. Вираз (1.3.2) справедливий, якщо нехтувати поляризаційною дисперсією. Коефіцієнт  виникає внаслідок того, що не завжди процес розповсюдження мод незалежний. За відповідних умов енергія одного коливання може перекачуватися в іншу моду і т. ін.
виникає внаслідок того, що не завжди процес розповсюдження мод незалежний. За відповідних умов енергія одного коливання може перекачуватися в іншу моду і т. ін.


