
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула для вычисления дисперсииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для вычисления дисперсии часто бывает удобно пользоваться следующей теоремой. Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания: D (X) = М (X 2) — [ M (X)]2. Доказательство. Математическое ожидание М (X)есть постоянная величина, следовательно, 2 М (X)и М 2(X)есть также постоянные величины. Приняв это во внимание и пользуясь свойствами математического ожидания (постоянный множитель, можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии: D (X)= М [ Х — М (X)]2= М [ Х 2 - 2 ХМ (X) + М 2(Х)]= = М (X 2) — 2 М (X) М (X) + М 2(X) = М (X 2) — 2 М 2(X) + М 2(X) = М (X 2) —M 2(X). Итак, D (X) =M (X 2) — [ М (Х)]2. Квадратная скобка введена в запись формулы для удобства ее запоминания. Пример 1. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
Решение. Найдем математическое ожидание М (X): М (Х) = 2 * 0, 1 + 3 * 0, 6 + 5 * 0, 3 = 3, 5. Напишем закон распределения случайной величины X 2:
Найдем математические ожидания М (X 2): M (X 2) = 4 * 0, 1 + 9 * 0, 6 + 25 * 0, 3 = 13, 3 Искомая дисперсия D (X) = М (X 2)—[ М (Х)]2= 13, 3 — (3, 5)2 = 1, 05. Замечание. Казалось бы, если X и Y имеют одинаковые возможные значения и одно и то же математическое ожидание, то идисперсии этих величин равны (ведь возможные значения обеих величин одинаково рассеяны вокруг своих математических ожиданий!).Однако в общем случае это не так. Дело в том, что одинаковые возможные значения рассматриваемых величин имеют, вообще говоря, различные вероятности, а величина дисперсии определяется на только самими возможными значениями, но и их вероятностями. Например, есливероятности «далеких» от математического ожидания возможных, значений X больше, чем вероятности этих же значений Y, и вероятности «близких» значений X меньше, чем вероятности тех же значений Y, то, очевидно, дисперсия X больше дисперсии Y. Приведем иллюстрирующий пример. Пример 2. Сравнить дисперсии случайных величин, заданных законами распределения:
Решение.Легко убедиться, что М (Х) = М (Y)= 0,97; D (X) Таким образом, возможные значения иматематические ожидания X и Y одинаковы, а дисперсии различны, причем D (X) > D (Y). Этот результат можно было предвидеть без вычислений, глядя лишь на законы распределений.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины С равна нулю: D (С) = 0. Доказательство. По определению дисперсии, D (C) =M {[ C-M (C)]2}. Пользуясь первым свойством математического ожидания (математическое ожидание постоянной равно самой постоянной), получим D (С)= М [(С—С)2] = М (0) = 0. Итак, D (С) = 0. Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D (CX) =C 2 D (X). Доказательство. По определению дисперсии имеем D (СХ) = М {[ СХ — М (СХ)]2}. Пользуясь вторым свойством математического ожидания (постоянный множитель можно выносить за знак математического ожидания), получим D (СХ) = М {[ СХ—СМ (X)]2} = М {С2 [ X — М (X)]2} = = С 2 М {[ Х — М (X)]2} = C 2 D (X). Итак, D (CX) = C 2 D (X). Свойство становится ясным, если принять во внимание, что при | С | > 1 величина СХ имеет возможные значения (по абсолютной величине), большие, чем величина X. Отсюда следует, что эти значения рассеяны вокруг математического ожидания М (СХ)больше, чем возможные значения X вокруг М (Х), т. е. D (CX) >D (X). Напротив, если0 < | С | < 1, то D (СХ)< D (X). Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D (X + Y) = D (X) + D (Y). Доказательство. По формуле для вычисления дисперсии имеем D (X + Y)= М [(X + Y)2]— [ М (X + Y)]2. Раскрыв скобки и пользуясь свойствами математического ожидания суммы нескольких величин и произведения двух независимых случайных величин, получим D (X + Y) = М [ X 2 + 2 ХY + Y 2] — [ M (X) + М (Y)]2= = М (X 2) + 2 М (X) • М (Y)+ М (Y 2) — М 2(X) —2 М (X) • М (Y) — M 2(Y) = { М (X 2) — [ М (X)]2} +{ M (Y 2) - [ M (Y)]2} =D (X) +D (Y). Итак, D (X + Y) = D (X) +D (Y). Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. Например, для трех слагаемых имеем D (X+Y+Z) =D [ X+ (Y+Z)] =D (X) +D (Y+Z) =D (X) +D (Y) +D (Z). Для произвольного числа слагаемых доказательство проводится методом математической индукции. Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины: D (C+X) =D (X). Доказательство. Величины С и X независимы, поэтому, по третьему свойству, D (C+X) =D (C) +D (X).
В силу первого свойства D (С)= 0. Следовательно, D (C+X) =D (X). Свойство становится понятным, если учесть, что величины X и X+С отличаются лишь началом отсчета и, значит, рассеяны вокруг своих математических ожиданий одинаково. Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D (X-Y) =D (X) +D (Y). Доказательство. В силу третьего свойства D (X-Y) =D (X) +D (-Y). По второму свойству, D (X—Y) = D (X) + (- 12) D (Y), или D (X — Y) = D (X) +D (Y).
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 899; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.01 с.) |

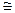 3, 69, D (Y)
3, 69, D (Y) 


