
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды дисперсий и правило их сложения. Свойства дисперсии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Свойство 1. Свойство 2. Свойство 3.
Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, приведенные в относительных величинах. Различают следующие относительные показатели вариации (V):
Коэффициент осцилляции ( отражает относительную колеблемость крайних значений признака вокруг средней
Линейный коэффициент вариации (): характеризует долю усреднённого значения абсолютных отклонений признака от средней величины
Коэффициент вариации (): используется для оценки типичности средних величин Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии. Выделяют: дисперсию общую межгрупповую внутригрупповую.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
где хо – общая средняя арифметическая для всей изучаемой совокупности. Межгрупповая дисперсия () характеризует систематическую вариацию, т. е. различия в величине изучаемого признака возникающие под влиянием признака-фактора, положенного в основание группировки. Рассчитывается по формуле:
где - ni – число единиц в определенной группе.
Внутригрупповая дисперсия () отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Рассчитывается по формуле:
На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий (): Указанные дисперсии взаимосвязаны между собой следующим равенством: величина общей дисперсии равна сумме средней из внутригрупповых и межгрупповой дисперсий:
В статистическом анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии - эмпирический коэффициент детерминации ():
Корень квадратный из эмпирического коэффициента детерминации – это эмпирическое корреляционное отношение ():
характеризует влияние признака, положенного в основание группировки (группировочного), на вариацию результативного признака.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 605; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.176 (0.009 с.) |

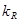 ):
): 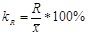
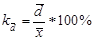


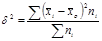
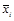 средняя по отдельной группе;
средняя по отдельной группе;
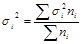



 = 0, то группировочный признак не оказывает влияния на результативный.
= 0, то группировочный признак не оказывает влияния на результативный. 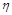 = 1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю.
= 1, то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю. 


