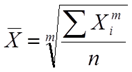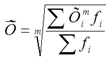Понятие о средних величинах, их значение. Виды средних величин и их расчет.

Средняя величина — это обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.

 

Объективность и типичность статистической средней обеспечивается лишь при определенных условиях.

Первое условие - средняя должна вычисляться для качественно однородной совокупности.
Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок.

Второе условие - для исчисле­ния средних должны быть использованы массовые данные.
В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности.

 

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.

 

При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.

 

 

Средние величины делятся на два больших класса:

 

степенные средние,
относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.

 

структурные средние.
рассматриваются мода и медиана.

Степенные средние в зависимости от представления исходных данных могут быть:

простыми

взвешенными

 

 

Простая средняя считается по несгруппированным данным и имеет следующий общий вид:

где

хi - варианта (значение) определенного признака,

m – показатель степени средней.

n – число вариант (значений).

Взвешенная средняя считается по сгруппированным данным и имеет вид:

 

где

хi - варианта (значение) определенного признака или серединные значения интервала, в котором измеряется варианта,

m – показатель степени средней.

fi – частота, показывающая сколько раз встречается i-е значение осредняемого признака.

 

Общие формулы расчета степенных средних имеют показатель степени m.

 

В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:

средняя гармоническая, если m = -1

средняя геометрическая, если m > 0

средняя арифметическая, если m = 1

средняя квадратическая, если m = 2

средняя кубическая, если m = 3

Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок.
Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

 

Средняя квадратическая применяется для расчета среднего квадратического отклонения (σ), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

 

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики.

Структурные средние. Их расчет в дискретном и интервальном рядах распределения.

Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вари­антами совокупности.

Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).

Для совокупности 3;4;2;4;3;3 мода равна 3

Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. Если число n вариант нечётно, то медиана равна варианте под номером (n + 1)/2