
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что называется корреляционным моментом двух случайных величин?Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математическое ожидание произведения отклонений этих величин Произведение плотностей распределения составляющих Дисперсия случайных величин Известная плотность распределения Дисперсия произведения случайных величин
173.Как определяется квадратичное отклонение σx случайной величины? A. Квадрат дисперсии B. Плотностью распределения C. Произведением этих величин D. Квадратный корень из дисперсии E. Корень квадратный из математического ожидания Чему равна вероятность того что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения? A. 0,9973 B. 0,2896 C. 0,1 D. 0,369 E. 0,95 175.Случайная величина X имеет дисперсию D (X) = 0,004. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,2, по неравенству Чебышева является выражение: A. 0,004/0,2 B. 1-0,004/0,2 C. 1-0,004-(0,2)2 D. (0.2)2/0.004 E. 1-0,004/(0,2)2
176.Случайная величина X имеет дисперсию D (X) = 1620. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 200, по неравенству Чебышева является выражение: A. 1+1620/2002 B. 1620/2002 C. 1-1620/2002 D. 2002/1620 E. 1-1620/200
177.Случайная величина X имеет дисперсию D (X) = 0,001. Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,1. A. 0,1 B. 1 C. 1,2 D. 2 E. 0,9+ 178.СВ Х является средним арифметическим независимых и одинаково распределенных случайных величин, дисперсия каждой из которых равна 5. Сколько нужно взять таких величин, чтобы СВ Х с вероятностью, не меньшей 0,9973, отклонялась от своего математического ожидания не более чем на 0,01? A. 450000 B. 45000 C. 4500 D. 450 179.Неравенство Чебышева справедливо для A. Дискретной и непрерывной величин B. Непрерывной величины C. Абсолютной величины D. Большой величины E. Малой величины 180.Формулировку центральной предельной теоремы дал A. Ляпунов А.М. B. Чебышев П.Л. C. Бернулли Я. D. Лаплас E. Чернышев Н.И 181.Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к:
A. Нормальному B. Среднему C. Предельному D. Бесконечному E. Нулю 182.Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы A. Ничтожное B. Максимальное C. Минимальное D. Среднее E. Общее 183.Теорема Чебышева является наиболее общим законом A. Малых чисел B. Больших чисел C. Дробных чисел D. Отрицательных чисел E. Простых чисел 184.Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа A. B. C. D(x) D. 0 E. 1 Среднее арифметическое достаточно большого числа независимо случайных величин (дисперсии которой равномерно ограничены) утрачивает характер A. Случайной величины B. Заданной величины C. Предельной величины D. Бесконечной величины E. Непрерывной величины 186.На теореме Чебышева основан широко применяемый в статистике: A. Метод пузырька B. Метод проверки статистических гипотез C. Метод расчета свободных характеристик выборки D. Выборочный метод E. Дисперсионный анализ Практически все значения нормально распределённой случайной величины лежат в интервале A. (-3 B. ( C. ( D. (-∞;+∞) E. (0:+∞) 188.Более строго-приблизительно с вероятностью значение нормально распределенной случайной величины которое лежит в интервале ( A. 0,9973 B. 0,95 C. 0,67 D. 0,7893 E. 0,0027
189Генеральным средним < variant>среднее арифметическое значений признака в генеральной совокупности <variant>среднее геометрическое значений признака в генеральной совокупности <variant>полусумму от минимального и максимального значений генеральной совокупности <variant>квадратный корень от произведения минимального и максимального значений генеральной совокупности <variant>полусумму от произведения минимального и максимального значений признака в группе
190.В ящике содержится 100 красных, 300 зеленых, 200 синих и 200 белых шаров. Из ящика наудачу извлекают 150 шаров. Объем выборки составляет... шаров.
<variant>150 <variant>100 <variant>200 <variant>800 <variant>300
191.Групповым средним называют: < variant>среднее арифметическое значений признака, принадлежащих группе <variant>квадратный корень от произведения минимального и максимального значений признака в группе <variant>среднее геометрическое значений признака, принадлежащих группе <variant>полусумму от минимального и максимального значений признака в группе <variant>полусумму от произведения минимального и максимального значений признака в группе
192.Выборочным средним <variant>квадратный корень от произведения минимального и максимального значений выборки <variant> среднее арифметическое значений признака в выборке <variant>полусумму от минимального и максимального значений выборки <variant>среднее геометрическое значений признака в выборке <variant>полусумму от произведения минимального и максимального значений признака в группе
193.Общее среднее можно рассчитать как: <variant >сумму групповых средних, умноженных на число объектов в группе, и полученную сумму разделить объем совокупности <variant>сумму групповых средних <variant>сумму групповых средних, умноженных на число объектов в группе <variant>квадратный корень от произведения групповых средних <variant>произведение групповых средних
194.Общим средним называют: <variant> среднее арифметическое значений признака, принадлежащих всей совокупности <variant>среднее геометрическое значений признака, принадлежащих всей совокупности <variant>полусумму от минимального и максимального значений признака в совокупности <variant>квадратный корень от произведения минимального и максимального значений признака в совокупности <variant>полусумму от произведения минимального и максимального значений признака в группе
195.Средним арифметическим чисел <variant> <variant> <variant> <variant> <variant> s w:val="22"/><w:shd w:val="clear" w:color="auto" w:fill="FFFFFF"/><w:lang w:val="EN-US"/></w:rPr><m:t>)/N</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
196.Несмещенной называется оценка параметра генеральной совокупности по выборочной, если: < variant>математическое ожидание параметра выборки равно оцениваемому параметру <variant>дисперсия параметра выборки равна нулю <variant> «исправленная» дисперсия параметра выборки не равна нулю <variant>дисперсия параметра выборки не равна оцениваемому параметру <variant> «исправленная» дисперсия параметра выборки равна нулю
197.Для оценки неизвестного генерального среднего используют: <variant>выборочное среднеквадратичное отклонение < variant>выборочное среднее <variant>выборочную дисперсию <variant> «исправленное» выборочное среднеквадратичное отклонение <variant>среднеквадратичное отклонение
198.В ящике содержится 100 красных, 300 зеленых, 200 синих и 200 белых шаров. Из ящика наудачу извлекают 150 шаров. Объем генеральной совокупности составляет... шаров. <variant>800 <variant>100 <variant>200 <variant>150
<variant>300
199.Среднее арифметическое значений признака генеральной совокупности называют. <variant>Средняя дисперсия <variant> Генеральная средняя <variant>Выборочная средняя <variant>Генеральная дисперсия <variant> Выборочная максимальная
200. Среднее арифметическое значение признака выборочной совокупности называют. <variant> Средняя дисперсия < variant>Выборочная средняя <variant> Генеральная средняя <variant> Генеральная дисперсия <variant> Выборочная максимальная
201.Среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения называют. <variant> Выборочная средняя <variant> Генеральная дисперсия <variant> Средняя дисперсия <variant> Генеральная средняя <variant> Выборочная максимальная
202.Квадратный корень из генеральной дисперсии называют <variant> Генеральным выборочным квадратическим отклонением <variant>Генеральным средним квадратическим отклонением <variant> Генеральным минимальным квадратическим отклонением <variant> Генеральным максимальным квадратическим отклонением <variant> Генеральным двойным квадратическим отклонением
203. Среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения называют. <variant> Выборочная средняя <variant>Выборочная дисперсия <variant> Генеральная дисперсия <variant> Средняя дисперсия <variant> Генеральная средняя
204. Квадратный корень из выборочной дисперсии называют. <variant> Генеральным средним квадратическим отклонением <variant>Выборочным средним квадратическим отклонением <variant>Выборочным максимальным квадратическим отклонением <variant>Выборочным минимальным квадратическим отклонением <variant> Генеральным двойным квадратическим отклонением
205. Генеральная совокупность задана таблицей распределения
Найти генеральную среднюю.??? <variant>4,5 <variant>4 <variant>5 <variant>6 <variant>7
206. Генеральная совокупность задана таблицей распределения
Найти генеральную дисперсию.??? <variant>1,8 + <variant>2,8 <variant>2,5 <variant>4,5 <variant>5,8
207.Выборочная совокупность задана таблицей распределения
Найти выборочную среднюю??? <variant>2+ <variant>3 <variant>3,8 <variant>3,5 <variant>2,5
208 Выборочная совокупность задана таблицей распределения
Найти выборочную дисперсию.???
<variant>2,5 <variant>3 <variant>4 <variant>1,5 <variant>1+
209<question>Даны р1=0,2, р2= 0,3, р3=0,5 и математическое ожидание М(х)=2,3. Найти возможное значение дискретной случайной величины х3, если х1=1,х2=2. <variant>-0,7. <variant>-3. <variant> <variant>4. <variant>3 +
210<question> Случайная величина Х задана функцией распределения
<variant>2. <variant> <variant> <variant>1. <variant>
211<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant> <variant>1. <variant>2.
212<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant>1. <variant> <variant>2.
213<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant> <variant>1. <variant>2.
214<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant>1. <variant> <variant>2.
215<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant>1. <variant> <variant>2
216<question> Случайная величина Х задана функцией распределения
<variant> <variant>1. <variant> <variant>2 <variant> 217<question>Из 50 рабочих норму выработки не выполняют 5 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму. <variant> <variant>
<variant>1. <variant> <variant>
218<question>Студент знает 15 из 20 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором два вопроса.
<variant> <variant> <variant>1. <variant> <variant>
219<question>В ящике лежат 10 лампочек, из которых 2 нестандартные. Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными. <variant> <variant> <variant> <variant> <variant>
220<question>Студент знает 20 из 25 вопросов программы. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором два вопроса. <variant> <variant> <variant> <variant>1. <variant>
221<question>Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут ровно 3. <variant>0,125. <variant>0,315. <variant>0,2048. ++ <variant>1,205. <variant>3,2.
222<question>Какова вероятность выпадения нечетного числа очков при бросании игральной кости? <variant>0,75. <variant>0,25. <variant>0,5. ++ <variant>0. <variant>1.
223<question> Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 5.
<variant>1. <variant>6. <variant> <variant> <variant>0,6.
224<question>В лабораторной клетке содержат трех белых и трех серых мышей. Найти число способов выбора двух мышей, если они могут быть любого цвета.
<variant>15++ <variant>16 <variant>9 <variant>18 <variant>13
225<question>Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны набрал их наудачу. Какова вероятность, что номер набран правильно? <variant> <variant> <variant> <variant>1 <variant>
226<question>Найдите математическое ожидание числа бракованных изделий в партии 5000, если каждое изделие может оказаться бракованным с вероятностью 0,02 <variant>120 <variant>100++ <variant>98 <variant>95 <variant>350
227<question>Найдите дисперсию числа бракованных изделий в партии 5000, если каждое изделие может оказаться бракованным с вероятностью 0,02 <variant>95 <variant>120 <variant>350 <variant>98++ <variant>100
228<question>В семье 5 детей. Найдите вероятность того, что среди этих детей 2 мальчика. Вероятность рождения мальчика принять равной 0,5. <variant> <variant> <variant> <variant>0,31 <variant>
229<question>В семье 5 детей. Найдите вероятность того, что среди этих детей 3 девочки. Вероятность рождения мальчика принять равной 0,5. <variant> <variant> <variant>0,3125 <variant> <variant>
<question>230.На ткацком станке нить обрывается в среднем 0,3 раза в течение часа работы станка. Вероятность того, что нить оборвется трижды за час, равна <variant> <variant> <variant> <variant>
<variant> 0
<question>231.Из колоды в 32 карты извлекают одну карту. Вероятность того, что извлеченная карта – туз, равна <variant> <variant> 0,4 <variant> 0,25 <variant> 0,2 <variant> 1
<question>232Автоматическая телефонная станция получает в среднем 3 вызова в минуту. Вероятность того, что станция получит 6 вызовов за данную минуту, равна <variant> <variant> <variant> <variant> <variant> 1
<question>233.Из колоды в 32 карты извлекают одну карту. Вероятность того, что она будет красной масти, равна <variant> <variant> <variant> <variant> <variant>
<question>234. Вероятность события может быть равна <variant> любому положительному числу <variant> любому числу из отрезка [0,1]++ <variant> любому числу <variant> любому числу отрезка [-1,1] <variant>
<question>235.Случайная величина распределена по нормальному закону, ее математическое ожидание равно 2, а дисперсия – 16. Тогда ее плотность распределения имеет вид??? <variant> <variant> <variant> <variant> <variant>
<question>236. Возводятся два жилых дома. Вероятность сдачи в срок одного из них 0,8, а другого – 0,9. Тогда вероятность сдачи в срок хотя бы одного дома равна A) 0,98++ B) 0,08 C) 0,72 D) 0,6 E) 0,81
<question>237. Среднеквадратическое отклонение дискретной случайной величины вычисляется по формуле A) B) C) D) E)
<question>238.Из каждых десяти билетов выигрышными являются два. Вероятность того, что среди пяти купленных наудачу билетов окажется два выигрышных, равна <variant> <variant> <variant> <variant> <variant> <question>239.Если известна вероятность события А, равная Р(<variant>, то вероятность противоположного события Р( <variant> <variant> 2 Р(А) <variant> 1 – 2 Р(<variant> <variant> 1 – Р(А) +++ <variant> 0
<question>240.Математическое ожидание непрерывной случайной величины – это <variant> <variant> <variant> <variant> <variant>
<question>241.Случайной величиной называется переменная величина, <variant> которая определяется совокупностью возможных значений +++ <variant> заданная функцией распределения <variant> значения которой зависят от случая и определена функция распределения <variant> которая является числовой характеристикой возможных исходов опыта <variant> значения которой заранее известны
<question>242.Случайная величина Х имеет нормальное распределение с плотностью распределения <variant> 36; 1: 6 <variant> 1; 6; 36 <variant> 6; 1; 1 <variant> 1; 36; 6 +++ <variant> 1;6;72
<question>243.В аквариуме плавают рыбки: 10 меченосцев и 6 вуалехвостов. Наугад ловится одна рыбка. Вероятность того, что это будет меченосец, равна <variant> 0,48 <variant> 0,5 <variant> 0,9 <variant> 0,625 +++ <variant> 0.6
<question>244.Вероятность достоверного события равна <variant> 1 ++ <variant> 0,75 <variant> <variant> любому числу <variant> 0
<question>245.Послано 6 радиосигналов. Вероятность приема каждого из них равна 0,9. Вероятность того, что будет принято 5 сигналов, равна <variant> <variant> <variant> <variant> <variant> 0.81
<question>246.Уравнение регрессии Y на Х, выраженное через коэффициент регрессии axy, имеет вид A) B) C) D) E)
<question>247.Для построения эмпирических прямых регрессии применяют метод наименьших квадратов+++ χ2 минимакса моментов метод наибольшего правдоподобия
<question>248.При проверке с помощью критерия χ2 гипотезы о равномерном распределении R(a,<variant>, когда концы интервала a и b известны, а число интервалов группировки равно m, статистика χ2 имеет распределение χ2 с числом степеней свободы??? m – 3 m m – 2 m – 1++++ m-4
<question>249 Наблюдения проводятся над системой (X: Y) двух случайных величин. Выборка состоит из пар чисел: (х1: y1), (х2: y2), …, (хn : yn). Найдены
нет верного ответа
<question>250Уравнение регрессии Y на Х, выраженное через коэффициент корреляции r, имеет вид??? a) b) c) d) e) <question>251Для построения доверительного интервала для дисперсии надо пользоваться таблицами F) нормального распределения G) распределения Стьюдента H) распределения Фишера I) распределения Пирсона ( J) распределением Фишера-Снедекора
<question>252Когда случайные величины называют коррелированными? F. Если их корреляционный момент отличен от нуля +++ G. Если их корреляционный момент равен нулю H. Если две величины зависимы I. Если заданная плотность равна нулю J. Если коэффициент корреляции равен нулю
<question>253 Когда случайные величины называют не коррелированными? Если их корреляционный момент равен нулю++ Если их корреляционный момент отличен от нуля Если две величины зависимы Если заданная плотность равна нулю Если коэффициент корреляции равен нулю <question> 254.Что называется корреляционным моментом двух случайных величин? Математическое ожидание произведения отклонений этих величин+++ Произведение плотностей распределения составляющих Дисперсия случайных величин Известная плотность распределения Дисперсия произведения случайных величин
<question> 255Как определяется квадратичное отклонение σx случайной величины? F. Квадратный корень из дисперсии+++ G. Квадрат дисперсии H. Плотностью распределения
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1778; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.40.24 (0.01 с.) |

 оказывала на сумму влияние:
оказывала на сумму влияние: , не меньше, чем???
, не меньше, чем??? +
+
 ;3
;3  ;
;  )+
)+ ;
;  )
)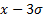 ;
;  )???
)??? называют:???
называют:??? называют:
называют: называют:???
называют:???




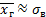



 .
. . Найти математическое ожидание случайной величины.
. Найти математическое ожидание случайной величины. ???
??? .
. .
. .
. ???
??? .
. . +
. + .
. ???
???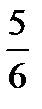 .
. . +
. + .
. ???
??? .
. .
. . ++
. ++ ???
??? . ++
. ++ .
. ???
??? .
. .
. ???
??? .++
.++ .++
.++ .
. .
. .
. .++
.++ .
.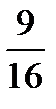 .
. .++
.++ .
. .
.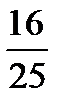 .
.
 .
. .++
.++ .
. .
. .++
.++ .
.



















 ++
++



 +++
+++






 +++
+++
 ) определяется как???
) определяется как??? Р(А)
Р(А)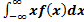 +++
+++



 . Тогда ее числовые характеристики М(Х), D(X) и
. Тогда ее числовые характеристики М(Х), D(X) и  равны соответственно???
равны соответственно???

 +++
+++

 +++
+++



 ,
, 
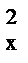 для хi и
для хi и  , S
, S  для yi (
для yi ( ). Тогда выборочный коэффициент корреляции rxy находится по формуле???
). Тогда выборочный коэффициент корреляции rxy находится по формуле??? +++
+++


 ++
++



 ) +++
) +++


