
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
A. Если их корреляционный момент отличен от нуляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Е) 28 80<test> Функция d) a) b) c) e)
81<test> Функция b) четной a) периодической c) нечетной d) обыкновенной e) возрастающей 82<test> Вероятность c) Интегральной теоремой Лапласа a) Пуассона b) Муавра - Лапласа
d) Бернулли e) Стьюдента 83<test> Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей a) 0,8882 b) 0,089 c) 0,882 d) 0,064 e) 0,8889 84<test> В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен равна 0,8. Найти вероятность того, что в данный момент включено 4 мотора a) 0,2457 b) 0,2405 c) 0,2416 d) 0,2451 e) 0,2401 85<test> В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен равна 0,8. Найти вероятность того, что в данный момент включены все моторы d) 0,2621 a) 0,2435 b) 0,2648 c) 0,2526 e) 0,2306 86<test> В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен равна 0,8. Найти вероятность того, что в данный момент выключены все моторы c) 0,000064 a) 0,0024 b) 0,00046 d) 0,0006 e) 0,064 87<test> Монету бросают 6 раз. Найти вероятность того, что герб выпадет менее двух раз d) a) b) c) e) 88<test> Величину, которая в результате испытания примет одно и только одно значение заранее не известное называют: a) случайной b) дискретной c) непрерывной d) законной e) нет правильного ответа a) возможные значения b) дискретные значения c) непрерывные значения d) случайные величины e) нет правильного ответа 90<test> Обозначения x1,x2,…,xn называют: a)дискретные значения b) возможные значения+ c) непрерывные значения d) случайные величины e) нет правильного ответа
91<test> Случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями называют: b) дискретной a) возможной c) непрерывной d) случайной e) равновозможной 92<test> Случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка называют: d) непрерывной a) возможной b) дискретной c) прерывной e) равновозможной
93<test> Таблицу чисел
Называют законом распределения: a) дискретной случайной величины b) возможной случайной величины c) непрерывной случайной величины d) случайной величины e) нет правильного ответа 94<test> В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 тенге и 10 выигрышей по 1 тенге. Найти закон распределения случайной величины. b)
a)
c)
d)
e)
95<test> Таблица в виде
задает: a) Биномиальное распределение b) Пуассоновское распределение c) Непрерывное распределение d) Распределение Коши e) Распределение Стьюдента
96<test> Составлен закон распределения
Правильно ли составлен закон распределения: a) нет; b) да; c) почти; d) почти да; e) нет правильного ответа; 97<test> Монета брошена два раза. Написать в виде таблицы закон распределения случайной величины х-числа выпадения герба: уточнить c)
a)
b)
d)
e) нет правильного ответа 98<test> Если распределение задано по формуле P a) Пуассоновское b) Бернулли c) Непрерывное d) Коши e) Распределение Стьюдента 99<test> В сосуд емкостью 10 л попала ровно одна болезнетворная бактерия. Какова вероятность зачерпнуть ее при наборе из этого сосуда стакана воды (200см3) A)0,02 B)0,01 C)0,03 D)0,04 E)0
100<test> Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредиться, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. a) 0,06131 b) 0,54881 c) 0,18045 d) 0,19537 e) 0,00004 101<test> Вероятность появления k событий на любом промежутке времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отчета называется свойством: a) стационарности b) ординарности c) простейшим d) интенсивностью e) потоком событий 102<test>
Распределение
Называется: a) Геометрическим b) Биномиальным c) Пуассоновским d) Гипергеометрическим e) Стьюдента 103<test> Из орудия производится стрельба по цели до первого попадания в цель, р=0,6. Найти вероятность того, что попадание произойдёт при третьем выстреле a) 0,096 b) 0,06 c) 0,1 d) 0,5 e) нет правильного ответа 104<test> В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найдите вероятность того, что оба шара белые. A)0,1 B)0,21 C)0,2 D)0,25 E)0,24
105<test> Среди 50 изделий 20 окрашеных. Найти вероятность того, что среди наудачу извлечённых 5 изделий окажется ровно 3 окрашенных: a) 0,2344 b) 0,2333 c) 0,2351 d) 0,2304 e) 0,2204
106<test> К числовым характеристикам случайной величины относится: a) математическое ожидание b) геометрическое ожидание c) поле ожидания d) непрерывность e) нет правильного ответа 107<test> По этой формуле M(X)= a) a) математическое ожидание дисперсия b) отклонение c) мода d) медиана 108<test> Найти математическое ожидание
a) 3,9 b) 4,0 c) 3 d) 2,5 e) 2,4 109<test> Производится 4 выстрела с вероятностью попадания в цель p1=0,6, p2=0,4, p3=0,7 и p4=0,5. Найти математическое ожидание общего числа попаданий. A)2,2 B)2,01 C)2,3 D)2,4 E)2,1
110<test> Математическое ожидание приближённо равно: a) среднему арифметическому; b) среднему геометрическому; c) медиане; d) моде; e) эксцессу
111<test> Математическое ожидание M(c)= a) c b) 0 c) 0,5 d) 0,1 e) 1 112<test> Постоянный множитель M(c*x)= a) M(c*x)=c*M(x) b) M(c*x)=0 c) M(c*x)=0,5 d) M(c*x)=c e) M(c*x)= M(x)
113<test> Математическое ожидание произведения M(X*Y)= a) M(X*Y)=M(X)*M(Y) b) M(X*Y)=0,5 c) M(X*Y)=0,1 d) M(X*Y)=M(X) e) M(X*Y)=0 114<test> Независимые случайные величины X и Y заданы следующими законами распределения
Найти математическое ожидание M(X*Y)= a) 32,56 b) 32 c) 30,46 d) 15,15 e) 30,58 115<test> M(X+Y)= a) M(X)+M(Y) b) M(X)+C c) M(Y)+C d) M(X)-M(Y) e) M(X)*M(Y)
116<test> Производится три выстрела с вероятностями попадания в цель, равными р1=0,4, р2=0,3. Р3=0,6. Найти математическое ожидание общего числа попаданий a) 1,3 b) 1 c) 1,2 d) 2 e) 1,5 117<test> Найти математическое ожидание суммы числа очков которые могут выпасть при бросании двух игральных костей a) 7 b) 5 c) 6 d) 3 e) 4 118<test> Математическое ожидание М(Х) числа появлений события А в n независимых испытаниях равно: a) n*p b) n*q c) n*p*q d) p*q e) n 119<test> Вероятность попадания в цель при стрельбе из орудия р=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов: a) 6 b) 5 c) 7 d) 4 e) 10 120<test> Разность между случайной величиной и её математическим ожиданием называют: a) средним квадратическим отклонением b) модой c) медианой d) отклонением e) дисперсией
121<test> M[X-M(X)]= a) 0 b) 1 c) 0,5 d) 0,25 e) 0,75 122<test>??? Закон распределения дискретной случайной величины Х
Найти математические ожиданияе отклонения: M[X-M(X)]=? a) 0,1 b) 0 c) 0,5 d) 0,4 e) 1 123<test>???
a) математическим ожиданием b) дисперсией c) отклонением d) модой E) нет правильного ответа 124<test> Дисперсия равна: a) b) M(x c) M(x-M(x)) d) e) 125<test> Найти дисперсию случайной величины 0.4+5.4+7.5-(0.2+1.8+1.5) 13.3-3.5
a) 1,05 b) 1 c) 0,8 d) 1,08 e) 1,8
126<test> Сравнить дисперсии случайных величин, заданных законами распределения
a) D(X)=D(Y) b) D(X)=D(Y)=2 c) D(X)<D(Y) d) D(X)>D(Y) e) D(X)≥D(Y) 127<test> Дисперсия постоянной величины D(C)= a) 0 b) 1 c) 0,5 d) 0,2 e) с 128<test> D(CX)= a) C b) CD(X) c) CD( d) C e) D(X) 129<test> Дисперсия суммы двух независимых случайных величин D(X+Y)= a) D(X)+D(Y) b) D(X)-D(Y) c) D(X)*D(Y) d) D(X)/D(Y) e) D(X)+2D(Y) 130<test> D(C+X)= a) D(X) b) D(X)+C c) D(X d) CD(X) e) C
131<test> D(X-Y)= a) D(X)+D(Y) b) D(X)-D(Y) c) D(X)*D(Y) d) D(X) e) D(X)/D(Y)
132<test> Дисперсия появления числа A в независимых испытаниях, в каждом из которых вероятность P появления события постоянна, равна: a) npq b) np c) nq d) pq e) n 133<test> Производится 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X-числа появлений события в этих испытаниях. a) 2,4 b) 2 c) 2,2 d) 3 e) 2,3 134<test>
a) средним квадратическим отклонением b) математическим ожиданием c) дисперсией d) начальным моментом e) центральным моментом
135<test> Найти среднее квадратичное отклонение, если D(X)=13,04 a) 3,61 b) 3 c) 3,15 d) 4 e) 3,5б
136<test>
a) начальным моментом порядка k b) средним отклонением порядка k c) центральным моментом порядка k d) модой е) эмпирическим моментом порядка k 137<test>
A) центральным моментом порядка k B) начальным моментом порядка k B)средним отклонением порядка k C) D)модой е) эмпирическим моментом порядка k 138<test>?????????
a) 0 b) 2 c) 0,5 d) 1 e) 0,25 139 <test> a) 1 b) 2 c) 0,5 d) 0 E) нет правильного ответа 140<test> Известны дисперсии двух независимых случайных величин D(x)=4, D(y)=3. Найти дисперсию суммы a) 7 b) 6 c) 5 d) 4 e) 8 141<test> Дисперсия случайной величины x равна 5. Найти дисперсию следующих величин x-1 a) 5 b) 6 b) 4 c) d) 3 e) 0 142<test> Дисперсия случайной величины x равна 5. Найти дисперсию 2x d) 20 a) 10 b) 15 c) 16 e) 25 143<test> Дисперсия случайной величины x равна 5. Найти дисперсию следующих величин 3x+6 E) 45 a) 40 b) 35 c) 30 d) 44 144<test> F(x)=P(X ‹ x) называют: a ) функцией распределения b) плотность распределения c) функцией Лагранжа d) функцией Лапласа e) интегралом распределения 145<test> Значения функции распределения принадлежат: c) [0;1] a) [0;1) b) (0;1) d) (0;1] e) (0;+∞)
146<test> Функция F(x) при выполнении F(x1) a) неубывающей b) убывающей c) возрастающей d) невозрастающей e) экстремальной
147<test> Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b) равна a) F(b)-F(a) b) F(b)F(a) c) F(b) d) F(a) e) F(b)+F(a)
148<test> f(x)=F’(x) называют: e) функцией распределения a) плотностью вероятности b) производной c) модой d) медианой 149<test> Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b) равна a) b) c) d) e) нет правильного ответа 150<test> a) функция распределения b) плотность вероятности c) мода d) медиана е) математическое ожидание
$$$ 151 Вычислите: А) 21 В) 35 С) D) 210 Е)
$$$152 Вычислите: А) 16 В) 4 С) D) 56 Е) 28
$$$153 В урне 18 шаров: 9 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны красный шар???? A) 0,25. B) C) 0. D) E)
$$$ 154 В ящике содержится 20 шаров, из них 6 красных, 4 синих и 10 белых. Найти вероятность того, что при случайном вынимании шар окажется цветным. А) В) С) D)5. E)1.
$$$155 В ящике содержится 20 шаров, из них 6 красных, 4 синих и 10 белых. Найти вероятность того, что при случайном вынимании шар окажется белым. А) В) С) D) 5. E) 1.
$$$156 Дано: Д (х)=2; Д (у)=5; и Z=2х – 3у. Найти: Д (z) Е) -11. А) 3. В) 53. С) -37. D) 19.
$$$157 Дано М(х) = 7 и М (y) = 9 и Z = 2х – 4y. Найти М (Z) А) -22. В) 50 С) -116. D) 172 Е) 2.
$$$158 Случайная величина Х задана функцией распределения
А) В) С)1. D) Е) 2.
$$$ 159 Математическое ожидание М(х) случайной величины Х, заданной законом распределения
определяется равенством????
A) B) C) D) E)
$$$ 160 Случайная величина Х распределена следующим законом:???
Найти М(Х)-? A) 2,4+ B) 2,6 C) 2,8 D) 0,76 E) 3,4
$$$161 Задумано двузначное число. Найти вероятность того, что задуманным числом окажется случайно названное двузначное число, цифры которого различны. А) 0,01. В) С) D) Е)81.
$$$162 Случайная величина Х задана функцией распределения
А) В) С)1. D) Е) 2.
$$$163 Случайная величина Х задана функцией распределения
А) В) С)1. D) Е) 2.
$$$ 164 Вычислите: А) 3 В) 6 С) D) Е) 9 $$$ 165 Вычислите: А) 3 В) 6+ С) 5 D) 7 Е) 9 $$$ 0166 На клумбе 5 синих, 6 красных, 4 желтых и 10 белых астр. Какова вероятность того, что наугад сорванная астра не будет белой. А) 15 В) 25 С) D)0,6 E)0,4 $$$167 На клумбе 5 синих, 6 красных, 4 желтых и 10 белых астр. Какова вероятность того, что наугад сорванная астра будет белой. А) 15 В) 25 С) D)0,6 E)0,4 $$$ 0168. Монета брошена два раза. Найти вероятность того, что, хотя бы один раз появится "герб". А) В)1 С)3 D) Е) $$$ 0169. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 7. А) В)1 С)6. D) Е)0,6
Корреляция нер-во Чебышева 170.Когда случайные величины называют коррелированными? A. Квадрат дисперсии B. Плотностью распределения A. 0,9973 B. 0,2896 C. 0,1 D. 0,369 E. 0,95 175.Случайная величина X имеет дисперсию D (X) = 0,004. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,2, по неравенству Чебышева является выражение: A. 0,004/0,2 B. 1-0,004/0,2 C. 1-0,004-(0,2)2 D. (0.2)2/0.004 E. 1-0,004/(0,2)2
176.Случайная величина X имеет дисперсию D (X) = 1620. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 200, по неравенству Чебышева является выражение: A. 1+1620/2002 B. 1620/2002 C. 1-1620/2002 D. 2002/1620 E. 1-1620/200
177.Случайная величина X имеет дисперсию D (X) = 0,001. Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,1. A. 0,1 B. 1 C. 1,2 D. 2 E. 0,9+ 178.СВ Х является средним арифметическим независимых и одинаково распределенных случайных величин, дисперсия каждой из которых равна 5. Сколько нужно взять таких величин, чтобы СВ Х с вероятностью, не меньшей 0,9973, отклонялась от своего математического ожидания не более чем на 0,01? A. 450000 B. 45000 C. 4500 D. 450 179.Неравенство Чебышева справедливо для A. Ляпунов А.М. B. Чебышев П.Л. C. Бернулли Я. D. Лаплас E. Чернышев Н.И 181.Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к: A. Нормальному B. Среднему C. Предельному D. Бесконечному E. Нулю 182.Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы A. Ничтожное B. Максимальное C. Минимальное D. Среднее E. Общее 183.Теорема Чебышева является наиболее общим законом A. Малых чисел B. Больших чисел C. Дробных чисел D. Отрицательных чисел E. Простых чисел 184.Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа A. B. C. D(x) D. 0 E. 1 A. Случайной величины B. Заданной величины C. Предельной величины D. Бесконечной величины E. Непрерывной величины 186.На теореме Чебышева основан широко применяемый в статистике: A. Метод пузырька D. Выборочный метод E. Дисперсионный анализ A. 0,9973 B. 0,95 C. 0,67 D. 0,7893 E. 0,0027
189Генеральным средним < variant>среднее арифметическое значений признака в генеральной совокупности <variant>среднее геометрическое значений признака в генеральной совокупности <variant>полусумму от минимального и максимального значений генеральной совокупности <variant>квадратный корень от произведения минимального и максимального значений генеральной совокупности <variant>полусумму от произведения минимального и максимального значений признака в группе
190.В ящике содержится 100 красных, 300 зеленых, 200 синих и 200 белых шаров. Из ящика наудачу извлекают 150 шаров. Объем выборки составляет... шаров. <variant>150 <variant>100 <variant>200 <variant>800 <variant>300
191.Групповым средним называют: < variant>среднее арифметическое значений признака, принадлежащих группе <variant>квадратный корень от произведения минимального и максимального значений признака в группе <variant>среднее геометрическое значений признака, принадлежащих группе <variant>полусумму от минимального и максимального значений признака в группе <variant>полусумму от произведения минимального и максимального значений признака в группе
192.Выборочным средним <variant>квадратный корень от произведения минимального и максимального значений выборки <variant> среднее арифметическое значений признака в выборке <variant>полусумму от минимального и максимального значений выборки <variant>среднее геометрическое значений признака в выборке <variant>полусумму от произведения минимального и максимального значений признака в группе
193.Общее среднее можно рассчитать как: <variant >сумму групповых средних, умноженных на число объектов в группе, и полученную сумму разделить объем совокупности <variant>сумму групповых средних <variant>сумму групповых средних, умноженных на число объектов в группе <variant>квадратный корень от произведения групповых средних <variant>произведение групповых средних
194.Общим средним называют: <variant> среднее арифметическое значений признака, принадлежащих всей совокупности <variant>среднее геометрическое значений признака, принадлежащих всей совокупности <variant>полусумму от минимального и максимального значений признака в совокупности <variant>квадратный корень от произведения минимального и максимального значений признака в совокупности <variant>полусумму от произведения минимального и максимального значений признака в группе
195.Средним арифметическим чисел <variant> <variant> <variant> <variant> <variant> s w:val="22"/><w:shd w:val="clear" w:color="auto" w:fill="FFFFFF"/><w:lang w:val="EN-US"/></w:rPr><m:t>)/N</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
196.Несмещенной называется оценка параметра генеральной совокупности по выборочной, если: < variant>математическое ожидание параметра выборки равно оцениваемому параметру <variant>дисперсия параметра выборки равна нулю <variant> «исправленная» дисперсия параметра выборки не равна нулю <variant>дисперсия параметра выборки не равна оцениваемому параметру <variant> «исправленная» дисперсия параметра выборки равна нулю
197.Для оценки неизвестного генерального среднего используют: <variant>выборочное среднеквадратичное отклонение < variant>выборочное среднее <variant>выборочную дисперсию <variant> «исправленное» выборочное среднеквадратичное отклонение <variant>среднеквадратичное отклонение
198.В ящике содержится 100 красных, 300 зеленых, 200 синих и 200 белых шаров. Из ящика наудачу извлекают 150 шаров. Объем генеральной совокупности составляет... шаров. <variant>800 <variant>100 <variant>200 <variant>150 <variant>300
199.Среднее арифметическое значений признака генеральной совокупности называют. <variant>Средняя дисперсия <variant> Генеральная средняя <variant>Выборочная средняя <variant>Генеральная дисперсия <variant> Выборочная максимальная
200. Среднее арифметическое значение признака выборочной совокупности называют. <variant> Средняя дисперсия < variant>Выборочная средняя <variant> Генеральная средняя <variant> Генеральная дисперсия <variant> Выборочная максимальная
201.Среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения называют. <variant> Выборочная средняя <variant> Генеральная дисперсия <variant> Средняя дисперсия <variant> Генеральная средняя <variant> Выборочная максимальная
202.Квадратный корень из генеральной дисперсии называют <variant> Генеральным выборочным квадратическим отклонением <variant>Генеральным средним квадратическим отклонением <variant> Генеральным минимальным квадратическим отклонением <variant> Генеральным максимальным квадратическим отклонением <variant> Генеральным двойным квадратическим отклонением
203. Среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения называют. <variant> Выборочная средняя <variant>Выборочная дисперсия <variant> Генеральная дисперсия <variant> Средняя дисперсия <variant> Генеральная средняя
204. Квадратный корень из выборочной дисперсии называют. <variant> Генеральным средним квадратическим отклонением <variant>Выборочным средним квадратическим отклонением <variant>Выборочным максимальным квадратическим отклонением <variant>Выборочным минимальным квадратическим отклонением <variant> Генеральным двойным квадратическим отклонением
205. Генеральная совокупность задана таблицей распределения
Найти генеральную среднюю.??? <variant>4,5 <variant>4 <variant>5 <variant>6 <variant>7
206. Генеральная совокупность задана таблицей распределения
Найти генеральную дисперсию.??? <variant>1,8 + <variant>2,8 <variant>2,5 <variant>4,5 <variant>5,8
207.Выборочная совокупность задана таблицей распределения
Найти выборочную среднюю??? <variant>2+ <variant>3 <variant>3,8 <variant>3,5 <variant>2,5
208 Выборочная совокупность задана таблицей распределения
Найти выборочную дисперсию.??? <variant>2,5 <variant>3 <variant>4 <variant>1,5 <variant>1+
209<question>Даны р1=0,2, р2= 0,3, р3=0,5 и математическое ожидание М(х)=2,3. Найти возможное значение дискретной случайной величины х3, если х1=1,х2=2. <variant>-0,7. <variant>-3. <variant> <variant>4. <variant>3 +
210<question> Случайная величина Х задана функцией распределения
<variant>2. <variant> <variant> <variant>1. <variant>
211<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant> <variant>1. <variant>2.
212<question> Случайная величина Х задана функцией распределения
<variant> <variant> <variant>1. <variant> <variant>2. <
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 972; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.110.45 (0.011 с.) |

 определятся формулой:
определятся формулой:
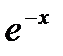



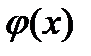 =
= 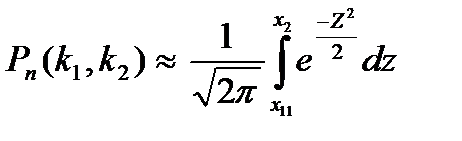 , где
, где 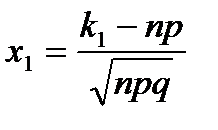 и
и  называется формулой:
называется формулой:


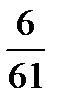


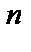
 *q
*q


 (k)=
(k)=  , то распределение называется:
, то распределение называется:
 определяется:
определяется: называется(может быть
называется(может быть  тогда ответ b, если нет, то е)
тогда ответ b, если нет, то е) +
+ -M(x))
-M(x))

 D(X)
D(X)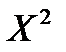 )
)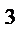 D(X)
D(X) называется:
называется: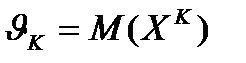 -случайной величины Х называют:
-случайной величины Х называют: случайной величины Х называют:
случайной величины Х называют: ?
?
 F(x2), если x2 ›x1 называется
F(x2), если x2 ›x1 называется



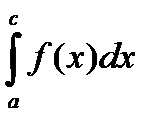

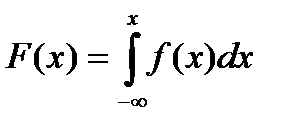 . По этой формуле вычисляется:
. По этой формуле вычисляется: ????
???? .
. .
. ???
??? .
. .
. .
. .
. .
.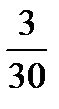 .
. .
. . Найти математическое ожидание случайной величины.???
. Найти математическое ожидание случайной величины.???
 .
. +.
+. .
.

 +
+

 . +
. + .
.

 . +
. + .
.
 .
. .
. ???
??? .
. ???
???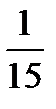


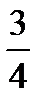
 +
+
 оказывала на сумму влияние:
оказывала на сумму влияние: , не меньше, чем???
, не меньше, чем??? +
+
 называют:???
называют:??? называют:
называют: называют:???
называют:???




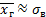



 .
. ???
??? .
. .
. ???
??? .
. . +
. + ???
???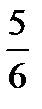 .
. . +
. + .
.


