
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент инерции. Твердое тело в механикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
2. Однородный металлический прут массой m и длиной l согнули в середине под прямым углом. Рассчитайте момент инерции полученного уголка относительно оси, перпендикулярной плоскости, в которой он лежит и проходящей через один из концов. 3. Рассчитайте момент инерции рамки из однородной проволоки в форме равностороннего треугольника относительно оси, перпендикулярной его плоскости и проходящей через середину одной из сторон. Масса рамки равна m, длина стороны – l. 4. Человек стоит на скамье Жуковского и ловит рукой мяч массой m = 0,4 кг, летящий в горизонтальном направлении со скоростью υ = 20 м/с. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6 кг·м2. 5. На скамейке Жуковского стоит человек и держит в руках стержень, расположенный вертикально по оси вращения. Скамейка с человеком вращается с угловой скоростью ω1 = 1 рад/с. С какой угловой скоростью ω2 будет вращаться скамейка с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамейки J = 6 кг·м2. Длина стержня L = 2,4 м, его масса m = 8 кг. Считать, что центр тяжести стержня с человеком находится на оси платформы. 6. Платформа, имеющая форму диска, может вращаться вокруг вертикальной оси без трения. На какой угол повернется платформа, если человек пойдет вдоль края платформы и обойдя ее, вернется на то же место платформы. Масса платформы 240 кг, масса человека – 60 кг. 7. На краю горизонтальной платформы, имеющей форму диска радиусом 4 м, стоит человек массой 80 кг. Масса платформы равна 240 кг и она может вращаться без трения вокруг вертикальной оси, проходящей через ее центр. С какой угловой скоростью будет вращаться платформа, если человек будет идти по ее краю со скоростью 2 м/с относительно нее? 8. К ободу однородного сплошного диска радиусом R =0,5 м приложена постоянная касательная сила F =100 Н. При вращении диска на него действует постоянный момент сил трения М тр=2 Н.м. Определить массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с2. 9. Вал в виде сплошного цилиндра массой
10. На барабан радиусом R = 20 см, момент инерции которого J = 0,1 кг·м2, намотан шнур, к концу которого привязан груз массой m = 0,5кг. Найти ускорение груза. 11. На барабан радиусом R = 0,2 м, момент инерции которого I = 0,1 кг·м2, намотан шнур, к которому привязан груз массой m = 0,5 кг. До начала вращения высота груза над полом h = 1м. Найти кинетическую энергию груза в момент удара о пол. 12. На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого J = 0,15 кг·м2, намотана легкая нить, к концу которой прикреплен груз массой m = 0,5 кг. До начала вращения барабана высота h груза над полом составляла 2,3 м. Определить: 1) время опускания груза до пола; 2) силу натяжения нити; 3) кинетическую энергию груза в момент удара о пол. 13. Две гири с массами m 1 = 2 кг и m 2 = 1 кг соединены нитью, перекинутой через блок массой m = 1 кг. Найти ускорение а, с которым движутся гири. Блок считать однородным диском. Трением пренебречь. 14. Блок массой m = 1 кг укреплен на конце стола. Гири 1 и 2 одинаковой массы m 1 = m 2 = 1 кг соединены нитью, перекинутой через блок. Гиря 2 находится на поверхности стола, а гиря 1 свешивается со стола. Коэффициент трения гири 2 о стол μ = 0,1. Найти ускорение, с которым движутся гири, и силы натяжения Т 1 и Т 2 нитей. Блок считать однородным диском. Трением в блоке пренебречь.
16. На наклонной плоскости находится груз m 1 = 5 кг, связанный нитью, перекинутой через блок, с другим грузом m 2 = 2 кг. Коэффициент трения между первым грузом и плоскостью k = 0,1; угол наклона плоскости к горизонту α = 37º. Определить ускорения грузов. При каких значениях m 2 система будет находиться в равновесии? 17. Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением ε = 0,4 рад/с2. Определить кинетическую энергию маховика через время t 2 = 25 с после начала движения, если через t 1 = 10 с после начала движения момент импульса L 1 маховика составлял 60 кг·м2/с. 18. Маховичок, момент инерции J которого равен 40 кг·м2, начал вращаться из состояния покоя под действием момента силы М = 20 Н·м. Вращение продолжалось в течение t = 10 с. Определить кинетическую энергию Е к, приобретенную маховичком. 19. Найти скорости υ движения центров масс шара, диска и полого цилиндра, скатившихся без скольжения с наклонной плоскости высотой h = 0,5 м. 20. Однородный шар скатывается без скольжения с плоскости, наклоненной под углом 150 к горизонту. За какое время он пройдет путь 2 м и какой будет его скорость в конце пути. 21. Пуля массой m = 10 г летит со скоростью 800 м/с, вращаясь около продольной оси с частотой ν = 3000 об/с. Принимая пулю за цилиндрик диаметра d = 8 мм, определить кинетическую энергию пули. 22. Карандаш, поставленный вертикально, падает на стол. Какую угловую и линейную скорости будет иметь в конце падения: 1) середина карандаша; 2) верхний конец? Длина карандаша 15 см. Какой импульс получит стол, если масса карандаша 50 г? 23. Шест длиной 2 м и массой 8 кг падает из вертикального положения на землю. Определить момент импульса шеста относительно точки опоры в момент удара о землю. 24. Шест длиной 2 м и массой 8 кг падает из вертикального положения на землю, так что нижний конец шеста не проскальзывает. Определить модуль момента импульса шеста относительно точки опоры и линейную скорость верхнего конца шеста в момент удара о землю. 25. Однородный шест длиной 3 м и массой 6 кг упал из вертикального положения на горизонтальную поверхность и остался на ней. Нижний конец шеста не двигался. Какой импульс передал шест поверхности? 26. Однородный стержень длиной l = 1 м подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую линейную скорость будет иметь нижний конец стержня в момент прохождения равновесного положения, если его отклонить на угол 60° от равновесного положения и отпустить? 27. Однородный стержень длины 1 м подвешен на горизонтальной оси, проходящей через верхний конец стержня. На какой угол надо отклонить стержень, чтобы при прохождении равновесного положения его нижний конец имел скорость 5 м/c? 28. Однородный шар скатывается без скольжения с плоскости, наклоненной под углом 150 к горизонту. За какое время он пройдет путь 2 м и какой будет его скорость в конце пути? 29. Вентилятор вращается со скоростью, соответствующей 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Работа сил торможения равна 44,4 Дж. Найти: 1) момент инерции вентилятора, 2) момент силы торможения. 30. Шарик массой m =50 г, привязанный к концу нити длиной L 1=1 м, вращается с частотой n 1= 1 об/с, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния L 2=0,5 м. С какой частотой n 2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. 31. Полый тонкостенный цилиндр массой m = 0,5 кг, катящийся без скольжения, ударяется о стену и отталкивается от нее. Скорость цилиндра до удара о стену v 1= 1,4 м/с, после удара v 1/ = 1 м/с. Определить выделившееся при ударе количество теплоты Q. 32. Какую работу надо совершить в течение t = 1 мин, чтобы увеличить частоту вращения маховика массой m = 0,5 кг, имеющего форму диска диаметром D = 1,5 м от ν0 = 0 до ν = 50 об/с, если к ободу маховика приложена касательная сила трения F тр = 1 Н? Механические колебания и волны 1. Материальная точка массой m = 5 г совершает гармоническое колебание с частотой ν = 5 Гц. Амплитуда колебаний А = 3 см. Определить максимальную силу F, действующую на точку, и полную энергию Е колеблющейся точки. 2. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2 с. Полная энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебания и наибольшее значение силы F max, действующей на частицу. 3. Полная энергия тела, совершающего гармоническое колебательное движение, равна 30 мкДж, максимальная сила, действующая на тело, равна 1,5 мН. Чему равно смещение тела от положения равновесия через 1,25 периода колебаний, если в начальный момент оно составляло 2 см. 4. Для определения ускорения а, с которым поднимается вертикально вверх ракета, в нее был помещен математический маятник длиной l, который при взлете совершил N полных колебаний за время t. Найти ускорение ракеты. 5. Математический маятник длиной 40 см и тонкий однородный стержень длиной 60 см совершают синхронные малые колебания вокруг горизонтальной оси. Найти расстояние от центра стержня до этой оси. 6. Диск радиусом R = 24 см колеблется относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период колебаний диска. 7. Уравнение колебаний физического маятника массой 0,2 кг и моментом инерции 0,4 кг·м2 имеет вид 8. На гвозде, вбитом в стену, в положении устойчивого равновесия висит квадратная рамка со стороной 20 см, сделанная из однородной тонкой проволоки. С каким периодом будут происходить её колебания после небольшого толчка? 9. Найти период вертикальных колебаний цилиндрического поплавка в воде, если в равновесом состоянии он погружен на 4 см. 10. Деревянный кубик плавает в воде, погрузившись в нее на 5 см. Слегка надавив на кубик, можно заставить его совершать колебания. С каким периодом они будут происходить? Сопротивлением воды можно пренебречь, ее плотность равна 1000 кг/м3. 11. Чему равен период колебаний деревянного кубика, плавающего в воде, если в равновесии он погружен в воду на 3/4. Плотность воды 103 кг/м3, длина ребра кубика 10 см. 12. Найти амплитуду А гармонического колебания, полученного сложением одинаково направленных колебаний, данных уравнениями 13. Амплитуда затухающих колебаний математического маятника за время t = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за t = 3 мин? 14. Амплитуда затухающих колебаний маятника за время t 1 = 1 мин уменьшилась втрое. Во сколько раз уменьшится амплитуда за время t = 5 мин? 15. Начальная амплитуда затухающих колебаний маятника А 0 = 3 см. Через t 1 = 10 с амплитуда стала А 1 = 1 см. Через какое время амплитуда станет равной А 2 = 0,3 см. 16. Чему равен логарифмический декремент затухания математического маятника длиной 1 м, если за 1 минуту амплитуда колебаний уменьшилась в 2 раза? 17. Найти логарифмический декремент затухания λ математического маятника, если за время t = 2 мин амплитуда колебаний уменьшилась в 4 раза. Длина маятника l = 1 м. 18. Математический маятник совершает затухающие колебания. Логарифмический декремент затухания λ = 0,01. За время t = 100 с амплитуда колебаний уменьшилась в 10 раз. Найти период затухающих колебаний. 19. Логарифмический декремент затухания колебаний маятника λ = 0,001. Определить число N полных колебаний, которое должен сделать маятник, чтобы амплитуда уменьшилась в 3 раза. 20. К пружине подвесили груз, в результате чего она удлинилась на х = 9 см. Каков будет период колебаний Т груза, если его немного оттянуть вниз и затем отпустить? Логарифмический декремент затухания λ = 0,3. 21. Сколько полных колебаний совершит гармонический осциллятор за время, в течение которого его энергияпосле начала колебаний уменьшится в 10 раз, если логарифмический декремент затухания λ = 0,03. 22. Тело массой m = 10 г совершает затухающие колебания. В течение времени t = 50 с оно потеряло 40% своей энергии. Определить коэффициент сопротивления r. 23. Тело массой m = 5 г совершает затухающие колебания. В течение времени t = 50 с тело потеряло 60% своей энергии. Определить коэффициент сопротивления r. 24. Тело массой m = 10 г совершает затухающие колебания. В течение времени t = 50 с оно потеряло 40% своей энергии. Определить коэффициент сопротивления r. 25. Гиря массой 500 г подвешена к спиральной пружине жесткостью 20 Н/м и совершает затухающие колебания с логарифмическим декрементом 0,004. Сколько колебаний должна совершить гиря, чтобы амплитуда колебаний уменьшилась в два раза? 26. Найти добротность математического маятника с длиной нити 20 см, у которого за 7 минут полная механическая энергия уменьшилась в 128 раз. 27. Складываются два гармонических колебания одного направления, описываемые уравнениями 28. Поперечная волна распространяется вдоль упругого шнура со скоростью υ = 10 м/с. Амплитуда колебаний точек шнура А = 5 см, а период колебаний Т = 1 с. Запишите уравнение волны и определите: 1) длину волны; 2) фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии х 1= 9 м от источника колебаний в момент времени t = 2,5 с. 29. Уравнение незатухающих колебаний имеет вид x = sin 2,5 30. Уравнение незатухающих колебаний имеет вид 31. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстоянии l = 4 см, в момент времени t =
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.011 с.) |

 1. Определить момент инерции правильного шестиугольника (R – сторона шестиугольника), в вершинах которого и в центре расположены точечные массы m относительно оси, перпендикулярной плоскости чертежа и проходящей через точку О.
1. Определить момент инерции правильного шестиугольника (R – сторона шестиугольника), в вершинах которого и в центре расположены точечные массы m относительно оси, перпендикулярной плоскости чертежа и проходящей через точку О.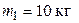 насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой
насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой  . С каким ускорением а будет опускаться гиря, если её предоставить самой себе?
. С каким ускорением а будет опускаться гиря, если её предоставить самой себе?
 15. Грузы массами 1 кг и 2 кг, привязаны к концам нити, перекинутой через блок в виде однородного диска массой 3 кг. Пренебрегая массой и растяжением нити, а также трением блока, найти изменение высоты грузов за вторую секунду после начала их движения.
15. Грузы массами 1 кг и 2 кг, привязаны к концам нити, перекинутой через блок в виде однородного диска массой 3 кг. Пренебрегая массой и растяжением нити, а также трением блока, найти изменение высоты грузов за вторую секунду после начала их движения. м. Определить расстояние от центра масс до точки подвеса маятника.
м. Определить расстояние от центра масс до точки подвеса маятника. , м и
, м и  , м.
, м. (см) и
(см) и 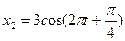 (см). Определите для результирующего колебания: 1) амплитуду; 2) начальную фазу. Запишите уравнение результирующего колебания и представьте векторную диаграмму сложения амплитуд.
(см). Определите для результирующего колебания: 1) амплитуду; 2) начальную фазу. Запишите уравнение результирующего колебания и представьте векторную диаграмму сложения амплитуд. t, см. Найти смещение x от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии l = 20 м от источника колебаний в момент времени t = 5 с. Скорость распространения колебаний u = 100м/с.
t, см. Найти смещение x от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии l = 20 м от источника колебаний в момент времени t = 5 с. Скорость распространения колебаний u = 100м/с. , см. Найти смещение из положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, в момент времени t = 0,01 с после начала колебаний. Скорость распространения колебаний равна с = 300 м/с.
, см. Найти смещение из положения равновесия точки, находящейся на расстоянии l = 75 см от источника колебаний, в момент времени t = 0,01 с после начала колебаний. Скорость распространения колебаний равна с = 300 м/с.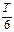 равно половине амплитуды. Найти длину λ бегущей волны.
равно половине амплитуды. Найти длину λ бегущей волны.


