
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механічний момент імпульсу та магнітний момент електронаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гіромагнітне відношення для орбітального руху електрона у атомі має вид
де m ¾ магнітний момент електрона, М ¾ його механічний, орбітальний момент імпульсу, е=1.6×10-19 Кл ¾ заряд електрона, а mе його маса. Власне значення
де
де m – магнітне квантове число. Відповідна проекція магнітного моменту дорівнює
Спін електрона
у два рази більше орбітального. Модуль
Проекція власного моменту на вісь Oz (вона співпадає з напрямком вектора магнітної індукції
у напрямку за полем чи проти поля. Значення власного магнітного моменту є
а його проекції
У загальному випадку результуючий момент імпульсу
Наприклад, для l=0
які відповідають паралельній та антипаралельній орієнтації вектора
Вираз для повного магнітного моменту повинен враховувати, що спінове гіромагнітне відношення у два рази більше орбітального й відповідні розрахунки дають
де g ¾ множник Ланде
Механічний та магнітний момент атома Результуючий момент імпульсу для багатоелектронної системи залежить від того, яка взаємодія моментів сильніша: спін-спінова й орбітально-орбітальна – LS - зв’язок, чи спін-орбітальна ¾ сильний jj-зв’язок. У першому випадку окремо об’єднуються спінові моменти електронів у МS, а орбітальні моменти у ML. Потім моменти MS і ML об’єднуються в сумарний момент атома MJ. Такий зв’язок зустрічається найчастіше і називається LS-зв’язком. Наведемо результати розрахунків для цього зв’язку. Величина орбітального моменту атома
де L ¾ орбітальне квантове число. Для двох електронів в атомі L=l1+l2, l1+l2-1, l1+l2-2,..., | l1-l2|, де l1, l2 ¾ орбітальні квантові числа електронів. Результуючий момент у цьому випадку може мати 2lmіn+1 значень, де lmіn ¾ менше з чисел l1 і l2. Якщо число електронів більше 2, то спочатку знаходиться найбільше значення L, яке дорівнює сумі всіх орбітальних квантових чисел електронів. Мінімальне значення L знаходяться шляхом додавання якихось двох моментів. Потім одержані результуючі значення складаються з третім моментом і т.д. Наступні значення L знаходяться послідовним відніманням від максимального числа одиниці аж до одержаного мінімального значення L. Проекція орбітального моменту на вісь Оz дорівнює МLz=mLћ, де mL=0, ±1,..., ±L. Результуючий спіновий момент МS ¾ може бути цілим або напівцілим числом у залежності від числа електронів в атомові. При парному числі електронів S приймає цілі значення від Моменти
де J= L+S, L+S-1, L+S-2,..., |L-S|. При парному числі електронів J¾ ціле число, при непарному ¾ J напівціле число. Проекція
де
а
де
є фактор Ландедля атома. Стан атома визначаються значеннями чисел L, S, J. Символіка станів записується у вигляді
Принцип Паулі
При розгляді багатоелектронних систем виявляються їхні особливості, яких не мають багаточастинні системи в класичній теорії. Один із фундаментальних принципів багатоелектронної системи є принцип нерозрізнюваності тотожних частинок ¾ частинок, що мають однакові фізичні властивості (маса, заряд, спін і т.п.). Ці частинки повністю втрачають свою індивідуальність. Якщо позначити сукупність квантових характеристик для кожної з частинки, наприклад, для системи з двох частинок через х1 та х2, то їх y-функція має вигляд y(х1,х2). У зв’язку з нерозрізнюваністю частинок можна записати |y(х1,х2)|2=|y(х2,х1)|2, при цьому можливі два випадки · · Як показують розрахунки, до першого випадку відносяться частинки з цілим спіном S=0,1,2... і такі частинки називаються бозонами. Їх статистичні властивості дослідили Ш.Бозе та А.Ейнштейн. Згідно статистики, названої їх іменами (статистика Бозе-Ейнштейна), в межах системи таких частинок у кожному з можливих станів може знаходитися необмежене число частинок. До другого випадку відносяться частинки з напівцілим спіном В багатоелектронних атомах взаємодія електронів із ядром носить складний характер і розрахунок їх станів в атомі дещо ускладнюється. Проте наближено їх стани можна характеризувати чотирма квантовими числами, так як це зроблено для атома водню. На підставі дослідних даних, ще до створення квантової теорії, в 1925 році В.Паулі сформулював закон, названий принципом Паулі. Згідно цього закону в будь-якому атомі не може бути два електрони, що знаходяться в одному стаціонарному стані, який визначається набором чотирьох квантових чисел: головного ¾ n, орбітального ¾ l, магнітного ¾ m, спінового ¾ ms. Класифікація станів багатоелектронних атомів відповідає класифікації станів атома водню, а електрони у стаціонарному стані атома наповнюють стани відповідно до значень квантових чисел.
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.007 с.) |

 , (1)
, (1) , а магнітний момент згідно (1) дорівнює
, а магнітний момент згідно (1) дорівнює , (2)
, (2) Дж/Тл ¾ магнетон Бора. Проекція орбітального моменту імпульсу
Дж/Тл ¾ магнетон Бора. Проекція орбітального моменту імпульсу , (3)
, (3) . (4)
. (4)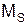 не зв’язаний з орбітальним рухом і визначає відповідний йому магнітний момент ms. Для цих моментів гіромагнітне відношення
не зв’язаний з орбітальним рухом і визначає відповідний йому магнітний момент ms. Для цих моментів гіромагнітне відношення (5)
(5) , а його величина дорівнює
, а його величина дорівнює . (6)
. (6) ) може мати лише два значення
) може мати лише два значення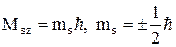 (7)
(7) ,
,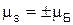 .
. складається з орбітального та спінового і його величина дорівнює
складається з орбітального та спінового і його величина дорівнює . (8)
. (8) , а при l відмінному від 0 буде два значення j
, а при l відмінному від 0 буде два значення j ,
, відносно осі Оz. Формула для проекції повного моменту така
відносно осі Оz. Формула для проекції повного моменту така . (9)
. (9) , (10)
, (10) . (11)
. (11)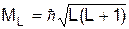 ,
, , коли всі моменти попарно компенсуються. При непарному числі електронів S ¾ напівціле. При непарному числі електронів S ¾ приймає всі напівцілі значення від
, коли всі моменти попарно компенсуються. При непарному числі електронів S ¾ напівціле. При непарному числі електронів S ¾ приймає всі напівцілі значення від 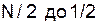 , коли лише один момент одного електрона залишається некомпенсованим.
, коли лише один момент одного електрона залишається некомпенсованим. створюють результуючий момент
створюють результуючий момент ,
, ,
, =0,±1,±2,..., ±J. Відповідні значення результуючого магнітного моменту атома записуються так
=0,±1,±2,..., ±J. Відповідні значення результуючого магнітного моменту атома записуються так ,
, ,
,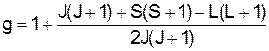
 , де під літерою L розуміють одну з літер S, P, D, F і т.п. в залежності від значення результуючого квантового числа L. Так при L=0, стан позначається літерою S, при L=1 буде стан Р, при L=2 буде стан D, при L=3 буде стан F і т.д. Наприклад, символ
, де під літерою L розуміють одну з літер S, P, D, F і т.п. в залежності від значення результуючого квантового числа L. Так при L=0, стан позначається літерою S, при L=1 буде стан Р, при L=2 буде стан D, при L=3 буде стан F і т.д. Наприклад, символ  означає стан із результуючим спіновим квантовим числом S=1/2. Значення S знайдено з рівняння 2S+1=2. Орбітальне квантове число L=1 і результуючим квантовим числом J=3/2. Виродження енергетичного стану дорівнює 2S+1 при S>L і 2L+1 при S<L.
означає стан із результуючим спіновим квантовим числом S=1/2. Значення S знайдено з рівняння 2S+1=2. Орбітальне квантове число L=1 і результуючим квантовим числом J=3/2. Виродження енергетичного стану дорівнює 2S+1 при S>L і 2L+1 при S<L. ¾ y-функція, яка симетрична відносно перестановки частинок місцями;
¾ y-функція, яка симетрична відносно перестановки частинок місцями; ¾ y-функція, яка антисиметрична відносно перестановки частинок місцями.
¾ y-функція, яка антисиметрична відносно перестановки частинок місцями. і вони називаються ферміонами. Їх статистику досліджували Е.Фермі та П.Дірак. Згідно статистики, названої їх іменами (статистика Фермі-Дірака), в межах системи таких частинок у кожному з можливих станів може знаходитися лише одна частинка.
і вони називаються ферміонами. Їх статистику досліджували Е.Фермі та П.Дірак. Згідно статистики, названої їх іменами (статистика Фермі-Дірака), в межах системи таких частинок у кожному з можливих станів може знаходитися лише одна частинка.


