
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенціальний бар’єрта його прозорістьСодержание книги
Поиск на нашем сайте
Нехай вільна частинка рухається вздовж осі ОХ в напрямку скінченого потенціального бар’єра U=U0 для 0£х£L і U=0 для (x<0, x>L) із енергією E£U0 (див.Мал.197 а)). Її рух задається плоскою y-хвилею. При падінні частинки на границю бар’єра, вона проникає в нього на деяку глибину хе (глибина, на якій імовірність зменшується в е раз) і з певною ймовірністю може пройти через нього наскрізь або відбитися від нього навіть при Е>U0. Для розв’язку цієї задачі з E<U0 потрібно скористатися відповідними умовами неперервності y-функції та її похідних на границях бар’єра. Відповідні розрахунки дають
Оцінка висоти проникнення електрона провідності над поверхнею металу показує, що при бар’єрі Для прямокутного бар’єра ймовірність D того, що частинка опиниться за бар’єром може бути представлена наближеним виразом
Для бар’єра довільної форми (див.Мал.197 б))
При подоланні потенціального бар’єра частинка начебто проходить через "тунель". Саме тому явище проходження частинкою бар’єра називають тунельним ефектом. Тунельний ефект дозволив пояснити цілий ряд фізичних явищ, які не мали пояснення з класичної точки зору. Зокрема, явище автоемісії, яке полягає в тому, що під дією сильного електричного поля, створеного при поверхні металу, спостерігається виліт електронів із металу. Таке поле перетворює потенціальний бар’єр на поверхні провідника в скінчений. В результаті стає можливим тунелювання електронів за поверхню металу. Квантування моменту імпульсу
Існує чотири квантові оператори, за допомогою яких визначається момент імпульсу частинки: оператор квадрата моменту імпульсу
має результатом власне значення
де l=0,1,2,...¾ азимутальне квантове число й модуль моменту імпульсу квантується
У сферичній системі координат (r,J,j)
і відповідне рівняння
Підстановкою y=eaj одержимо
а розв’язком буде Умовою однозначності розв’язку є y(j+2p)=y(j), тобто
Ця умова виконується якщо покласти Момент імпульсу системи частинок дорівнює сумі моментів цих частинок, яка також квантується і записується у вигляді
Воднеподібні атоми
До воднеподібних атоміввідносяться власне водень та група одновалентних лужних елементів, однократно іонізований атом гелію
де r ¾ відстань електрона від ядра. При цьому рівняння Шредінгера запишеться так
Зважаючи на сферичну симетрію воднеподібних атомів, вводяться сферична система координат і в ній рівняння Шредінгера записується у виді
Не приводячи у явному вигляді вираз лапласіана
В (3) · n=1,2,3,… ¾ головне квантове число, що визначає енергію електрона у атомі та ймовірність знаходження електрона на відстані r від ядра. Усі електрони атома з однаковим головним квантовим числом формують його енергетичну оболонку. · l=0,1,2,…,n-1 – азимутальне (орбітальне) квантове число, що визначає момент імпульсу електрона у атомі. Азимутальне квантове число формує підоболонку електронів з однаковим моментом імпульсу. · m=0, ± 1, ± 2,..., ± l – магнітнеквантове число, що визначає проекцію моменту імпульсу на вісь а). Власні значення енергії. Власне значення енергії електрона в полі ядра дискретне і має вигляд
а для електрона не зв’язаного з ядром енергія Е>0 і неперервна. Найменша величина енергії водню
Використовуючи (2) можна записати
Число N можливих станів у межах енергетичної оболонки визначається сумою Nm по всім можливим значенням l
і знаходиться як сума n членів арифметичної прогресії з різницею d=3, першим членом а1=1 та n-м членом аn=2n-1
Усі можливі стани атома водню класифікуються умовними позначеннями через позначення енергетичних оболонок n та їх підоболонок l за схемою, поданою в таблиці. Випромінювання та поглинання світла атомом відбувається з певними обмеженнями, які ще називають правилами відбору.
Виявляється, що при переходах електрона між енергетичними рівнями, у першому наближенні, повинно відбуватися таке обмеження на азимутальне квантове число l Dl=±1, (5) яке пов’язане із законом збереження імпульсу, коли враховані імпульси атома й фотона, що випромінюється чи поглинається. Таким чином в атомі можливі переходи nsÛmp, npÛmd і т.п.
б). Власні функції. Власні функції Наведемо декілька значень радіальної та сферичної функцій, поклавши
1. Для частинки у глибокій потенціальній ямі для енергії справджуються такі співвідношення
2. Для гармонічного осцилятора можна записати
3. Для воднеподібних атомів. У випадку n+1-го енергетичного рівня маємо
а відносний проміжок становитиме
В усіх перелічених випадках при великих числах n (n>>1) маємо Одержаний результат є окремим випадком загального принципу відповідності Бора, який він установив в 1923 році стосовно квантової механіки. За цим принципом будь-яка нова, більш узагальнена теорія природних явищ у фізиці, що є розвитком класичної теорії, не відкидає останньої узагалі, а містить її у собі у певних межах застосування, причому у граничних випадках нова теорія переходить у попередню. Так, наприклад, при малих швидкостях тіл V<<c, релятивістська механіка переходить у класичну, а при
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.194.30 (0.008 с.) |

 .
. електрони виходять із метала на висоту xe»0.1 нм.
електрони виходять із метала на висоту xe»0.1 нм. .
.
 .
. , та три оператори проекцій імпульсу ¾
, та три оператори проекцій імпульсу ¾  . Згідно принципу невизначеностей, одночасно можуть бути визначені лише квадрат моменту та одна з його проекцій. Розв’язок операторного рівняння
. Згідно принципу невизначеностей, одночасно можуть бути визначені лише квадрат моменту та одна з його проекцій. Розв’язок операторного рівняння
 ,
, .
.
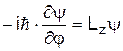 .
. і
і  ,
, .
. .
. , де m=0,±1,±2,±3,...¾ магнітне квантове число. Проекція не може бути більша величини вектора, тобто L>Lz і
, де m=0,±1,±2,±3,...¾ магнітне квантове число. Проекція не може бути більша величини вектора, тобто L>Lz і  , тобто найбільше значення m дорівнює l: m=0,±1,±2,±3,...±l.
, тобто найбільше значення m дорівнює l: m=0,±1,±2,±3,...±l. , де L ¾ азимутальне квантове число системи частинок. Найбільше значення L буде коли моменти мають один напрямок і найменше при протилежних напрямках моментів частинок. Наприклад, якщо система складається з двох частинок, то L=l1+l2, l1+l2-1,...,| l1-l2|.
, де L ¾ азимутальне квантове число системи частинок. Найбільше значення L буде коли моменти мають один напрямок і найменше при протилежних напрямках моментів частинок. Наприклад, якщо система складається з двох частинок, то L=l1+l2, l1+l2-1,...,| l1-l2|. , двічі іонізований атом літію
, двічі іонізований атом літію  і т.п. Потенціальна енергія електрона у таких атомах у полі ядра із зарядом Ze записується у вигляді
і т.п. Потенціальна енергія електрона у таких атомах у полі ядра із зарядом Ze записується у вигляді ,
, . (1)
. (1) . (2)
. (2) у сферичній системі координат, вкажемо, що розв’язок рівняння (2) знаходиться у вигляді
у сферичній системі координат, вкажемо, що розв’язок рівняння (2) знаходиться у вигляді (3)
(3) ¾ радіальна хвильова функція,
¾ радіальна хвильова функція,  ¾ сферична хвильова функція. Числа n,l,m мають назву квантових чисел:
¾ сферична хвильова функція. Числа n,l,m мають назву квантових чисел: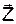 , яку ототожнюють із напрямком вектора магнітної індукції
, яку ототожнюють із напрямком вектора магнітної індукції  зовнішнього електромагнітного поля.
зовнішнього електромагнітного поля. , (1)
, (1) буде при n=1 і
буде при n=1 і (2)
(2) . (3)
. (3) (4)
(4)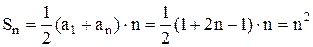 .
.
 є добутком двох множників
є добутком двох множників  . Множник
. Множник  є розв¢язком радіальної частини рівняння Шредінгера, ядром якого є функція Лагерра. Цей множник залежить від квантових чисел n, l. Сферична функція
є розв¢язком радіальної частини рівняння Шредінгера, ядром якого є функція Лагерра. Цей множник залежить від квантових чисел n, l. Сферична функція  є розв¢язком частини рівняння Шредінгера, яка залежить від кутів
є розв¢язком частини рівняння Шредінгера, яка залежить від кутів  і визначається квантовими числами l, m. Можна показати, що функція
і визначається квантовими числами l, m. Можна показати, що функція  і його проекції
і його проекції 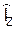 . Густина ймовірності знаходження електрона на відстані r від ядра задається виразом
. Густина ймовірності знаходження електрона на відстані r від ядра задається виразом  і для декількох функцій на малюнку 13 наведена відповідна її залежність від r у мірилі борівського радіуса
і для декількох функцій на малюнку 13 наведена відповідна її залежність від r у мірилі борівського радіуса  . З малюнка видно, що найбільш імовірними є відстані від ядра, що співпадають із радіусами відповідних борівських орбіт.
. З малюнка видно, що найбільш імовірними є відстані від ядра, що співпадають із радіусами відповідних борівських орбіт. (див.Мал.199)
(див.Мал.199) ,
,  ,
, .
. ,
,  ,
,  ,
,  .
. в). Принцип відповідності Бора. Розглянемо одну спільну властивість енергій електрона, що знаходиться у потенціальній ямі, електрона, що здійснює гармонічні коливання (осцилятор) та, на кінець, електрона у воднеподібному атомі. Знайдемо відносні проміжки енергій електронів для перелічених випадків.
в). Принцип відповідності Бора. Розглянемо одну спільну властивість енергій електрона, що знаходиться у потенціальній ямі, електрона, що здійснює гармонічні коливання (осцилятор) та, на кінець, електрона у воднеподібному атомі. Знайдемо відносні проміжки енергій електронів для перелічених випадків. ,
,  ,
,  .
. ,
,  ,
, 
 ,
, .
. й енергія стає неперервною. Це означає, що починаючи з деяких значень квантових чисел, енергія частинки може розглядатися як класична.
й енергія стає неперервною. Це означає, що починаючи з деяких значень квантових чисел, енергія частинки може розглядатися як класична. квантова механіка переходить у класичну.
квантова механіка переходить у класичну.


