
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суперпозиція станіву квантовій механіціСодержание книги
Поиск на нашем сайте
У квантовій механіці кожній фізичній величині зіставляється оператор
Оператор Гамільтона приписує, що для знаходження повної енергії частинки, потрібно скласти диференціальне рівняння
і розв’язати його, знайшовши Е і y. Узагалі для будь-якого оператора складається диференціальне рівняння
яке розв’язується при відповідних крайових умовах. Розв'язок дає власні значення q1,q2,q3...qn... та власні функції y1,y2,y3...yn.... Вимірювання величини q можуть показати, що вона завжди має певне значення, а може статися, що в різних вимірюваннях будуть різні значення q. У першому випадку кажуть, що q має певне значення, а у другому випадку ¾ величина q із різною ймовірністю приймає відповідні значення зі свого спектра, а y -функція такого стану може бути записана у вигляді суперпозиції власних функцій
причому, функції
Тепер можна записати
Квадрат модуля
Рух вільної частинки
Рух вільної частинки характеризується сталою швидкістю V, а повна енергія Е є кінетичною енергією. Направимо вісь Ох уздовж напрямку руху. Стаціонарне рівняння Шредінгера тепер матиме вигляд
де
Повним розв’язком рівняння Шредінгера буде
де
а величина |Y|2=|A|2 не залежить від часу t.
Частинка у нескінченно глибокій потенціальній ямі
Нехай електрон знаходиться в одновимірній потенціальній ямі шириною L із потенціальною енергією U=0 для 0<x<L і U=¥ для (x£0, x³L), причому граничні умови для y-функції зводяться до y=0 при x£0 і x³L. Стаціонарне рівняння Шредінгера для електрона в ямі буде мати вигляд рівняння для вільного електрона
де y=Asіn(kx+a). (3) Знайдемо сталі A та a із граничних умов. З умови y(x=0)=Asіna=0 (4) слідує a=0, а з умови y(x=L)=Asіn(kL)=0 слідує knL=np
Останній вираз означає, що на ширині ями L повинно вкладатися ціле число півхвиль де Бройля. Основним висновком із розв’язку даної задачі є те, що обмеження руху електрона у просторі призводить до виникнення дискретності його енергії. Із
Крок дискретності енергії для електрона дорівнює
Для електрона в ямі з L=10-9 м DЕn=0.377 еВ, а для макроскопічної ями з L=10-2 м=1 см маємо DЕn=3.77×10-15 еВ і спектр енергій квазінеперервний. Розподіл імовірності знаходження частинки в ямі задається виразом y= З умови нормування
знайдемо
Остаточно розв’язок має вигляд
Густина імовірності знаходження електрона в точці х пропорційна Покажемо, що функції
де функція
Доведемо (1) у явному виді. Підставимо у (1) значення функцій і проведемо очевидні перетворення.
При
Тепер
При n=m
Тепер
Вирази (11-12) доводять співвідношення ортонормованості Y-функцій (10). Гармонічний осцилятор
В одновимірному просторі стаціонарне рівняння Шредінгера для осцилятора можна записати у вигляді
Скінчений, однозначний і неперервний розв’язок цього рівняння існує при умові, що
Найменше значення енергії осцилятора, яке дорівнює Принцип відповідності. В 1923 році Н.Бор установив принцип відповідності, що вимагає перехід наслідків квантової механіки в класичні при ћ®0. Іншими словами в цьому випадку квантово-механічний опис явищ повинен співпадати з класичним. Зокрема, у граничному наближенні до великих квантових чисел квантовий опис також повинен співпадати з класичним.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.77.119 (0.006 с.) |

 , який описує сукупність математичних операцій, за якими можна обчислити його власне значення та відповідну власну y-функцію. У стаціонарному рівнянні Шредінгера можна визначити енергетичний оператор, власними значеннями якого є енергія частинки Е. Такий оператор називається оператором Гамільтона і він має вид
, який описує сукупність математичних операцій, за якими можна обчислити його власне значення та відповідну власну y-функцію. У стаціонарному рівнянні Шредінгера можна визначити енергетичний оператор, власними значеннями якого є енергія частинки Е. Такий оператор називається оператором Гамільтона і він має вид . (1)
. (1) (2)
(2) , (3)
, (3) , (4)
, (4) є ортонормованими
є ортонормованими
 . (5)
. (5)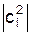 визначає ймовірність того, що при вимірюванні буде одержане значення власної величини q=qі.
визначає ймовірність того, що при вимірюванні буде одержане значення власної величини q=qі. , (1)
, (1) ¾ хвильове число. Розв’язком цього рівняння є хвильова функція
¾ хвильове число. Розв’язком цього рівняння є хвильова функція . (2)
. (2) , (3)
, (3) . Таким чином рух вільної частинки у квантовій механіці описується плоскою монохроматичною хвилею. При розповсюдженні частинки в напрямкові Ох
. Таким чином рух вільної частинки у квантовій механіці описується плоскою монохроматичною хвилею. При розповсюдженні частинки в напрямкові Ох ,
, . (5)
. (5) . (6)
. (6)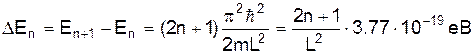 (7)
(7) , а максимуми її для кожного з n знаходяться в точках
, а максимуми її для кожного з n знаходяться в точках  , де m=1,2,...,n-1. В той же час із класичної точки зору знаходження частинки в кожній точці простору ями рівно ймовірне.
, де m=1,2,...,n-1. В той же час із класичної точки зору знаходження частинки в кожній точці простору ями рівно ймовірне.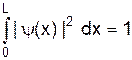 (8)
(8) .
. . (9)
. (9) і вона вона представлена на графіку Мал.195.
і вона вона представлена на графіку Мал.195. є ортонормованими, тобто задовольняють співвідношенням
є ортонормованими, тобто задовольняють співвідношенням , (10)
, (10)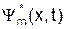 є комплексно спряженою до функції
є комплексно спряженою до функції  .
.

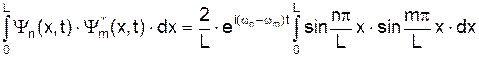



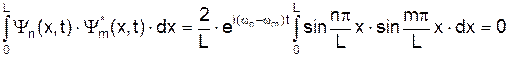 . (11)
. (11)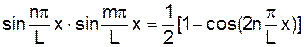 ,
, 
 ,
,  .
. . (12)
. (12) Гармонічним осцилятором називають частинку, що здійснює гармонічні коливання під дією пружної сили
Гармонічним осцилятором називають частинку, що здійснює гармонічні коливання під дією пружної сили  , де k¾ коефіцієнт пружності. Потенціальна енергія осцилятора
, де k¾ коефіцієнт пружності. Потенціальна енергія осцилятора 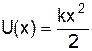 (див.Мал.196), а власна частота
(див.Мал.196), а власна частота 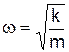 , де m ¾ маса частинки, тобто
, де m ¾ маса частинки, тобто .
. .
. .
. , називають нульовою енергією осцилятора і вона визначає його енергію при температурі Т=0 К, тобто при Т=0 К частинки, що знаходяться у вузлах кристалічної решітки здійснюють нульові коливання. Результати дослідів по розсіюванню світла в кристалах при ТÞ0 підтверджують цю тезу.
, називають нульовою енергією осцилятора і вона визначає його енергію при температурі Т=0 К, тобто при Т=0 К частинки, що знаходяться у вузлах кристалічної решітки здійснюють нульові коливання. Результати дослідів по розсіюванню світла в кристалах при ТÞ0 підтверджують цю тезу.


