
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи атомної фізики та квантової механіки.Содержание книги
Поиск на нашем сайте
Елементи атомної фізики та квантової механіки.
Хвильова y-функціяЛуї де Бройля та її фізичний зміст Наявність хвильових властивостей у частинок, що рухаються ставить питання про фізичний зміст їх хвильових функцій, які було названо
і
і
тобто групова швидкість хвилі дорівнює швидкості частинки У дослідах по дифракції електронів у різних точках простору спостерігалось більше чи менше скупчення електронів, що відповідало різним значенням інтенсивності хвиль де Бройля. Це означає наявність певної ймовірності знаходження електрона в точках простору, яка характеризується густиною ймовірності і яка зв’язана з інтенсивністю хвиль де Бройля. В 1926 р М.Борн сформулював такий фізичний зміст хвиль де Бройля: квадрат модуля псі-функції визначає густину ймовірності dР того, що частинка знаходиться в елементі об’єму dV=dx×dy×dz, обмеженого координатами x, x+dx;y, y+dy; z, z+dz,
За допомогою y-функції можна обчислити середні значення величин, які характеризують стан частинки, наприклад, для середнього значення відстані електрона від ядра можна записати вираз
Псі-функція повинна бути нормованою
Нормованість псі-функції означає, що ймовірність знаходження частинки в наданому їй об'ємі V дорівнює 1. Рівняння Шредінгера
У класичній механіці рівняння руху за другим законом Ньютона розв’язується основна задача механіки: за заданими силами, що діють на макроскопічне тіло, та початковими умовами для координат та швидкості, знаходяться координати й швидкість тіла в будь-який момент часу. Подібним рівнянням, у квантовій механіці є хвильове рівняння Шредінгерадля
визначає хвильову функцію де Бройля
¾ оператор Лапласа. На Y-функцію накладаються такі умови: а) вона має бути скінченою, однозначною та неперервною разом із своїми першою та другою похідними по x,y,z,t; б) функція |Y|2, яка має фізичний зміст імовірності, має бути інтегрованою, тобто такою, що інтеграл Записане хвильове рівняння Шредінгера, називається часовим: в ньому потенціальна енергії може залежати від часу t. Якщо потенціальна енергія не залежить від часу, то
де Е ¾ повна енергія частинки. Дійсно, підстановка (2) у рівняння Шредінгера (1) приводить його до рівняння
яке називається стаціонарним рівнянням Шредінгера, так як воно у явному виді не залежить від t. Розв'язок рівнянь (1) та (3) означає, що через вираз для функції Коротко зупинимось на властивостях рівняння Шредінгера - хвильові функції повинні бути однозначними та неперервними в усьому просторі, навіть коли Потенціальна енергія буде мати поверхні розриву; - частинка не може проникнути у ту область, де - хвильові функції повинні бути скінченими, якщо U стає нескінченною; - хвильові функції повинні мати неперервними першу та другу похідні; - при від'ємному значенні потенціальної енергії U енергія частинки дискретна й від'ємна, а енергетичні рівні згущуються у напрямку до рівня з Е=0.
Рух вільної частинки
Рух вільної частинки характеризується сталою швидкістю V, а повна енергія Е є кінетичною енергією. Направимо вісь Ох уздовж напрямку руху. Стаціонарне рівняння Шредінгера тепер матиме вигляд
де
Повним розв’язком рівняння Шредінгера буде
де
а величина |Y|2=|A|2 не залежить від часу t.
Гармонічний осцилятор
В одновимірному просторі стаціонарне рівняння Шредінгера для осцилятора можна записати у вигляді
Скінчений, однозначний і неперервний розв’язок цього рівняння існує при умові, що
Найменше значення енергії осцилятора, яке дорівнює Принцип відповідності. В 1923 році Н.Бор установив принцип відповідності, що вимагає перехід наслідків квантової механіки в класичні при ћ®0. Іншими словами в цьому випадку квантово-механічний опис явищ повинен співпадати з класичним. Зокрема, у граничному наближенні до великих квантових чисел квантовий опис також повинен співпадати з класичним.
Воднеподібні атоми
До воднеподібних атоміввідносяться власне водень та група одновалентних лужних елементів, однократно іонізований атом гелію
де r ¾ відстань електрона від ядра. При цьому рівняння Шредінгера запишеться так
Зважаючи на сферичну симетрію воднеподібних атомів, вводяться сферична система координат і в ній рівняння Шредінгера записується у виді
Не приводячи у явному вигляді вираз лапласіана
В (3) · n=1,2,3,… ¾ головне квантове число, що визначає енергію електрона у атомі та ймовірність знаходження електрона на відстані r від ядра. Усі електрони атома з однаковим головним квантовим числом формують його енергетичну оболонку. · l=0,1,2,…,n-1 – азимутальне (орбітальне) квантове число, що визначає момент імпульсу електрона у атомі. Азимутальне квантове число формує підоболонку електронів з однаковим моментом імпульсу. · m=0, ± 1, ± 2,..., ± l – магнітнеквантове число, що визначає проекцію моменту імпульсу на вісь а). Власні значення енергії. Власне значення енергії електрона в полі ядра дискретне і має вигляд
а для електрона не зв’язаного з ядром енергія Е>0 і неперервна. Найменша величина енергії водню
Використовуючи (2) можна записати
Число N можливих станів у межах енергетичної оболонки визначається сумою Nm по всім можливим значенням l
і знаходиться як сума n членів арифметичної прогресії з різницею d=3, першим членом а1=1 та n-м членом аn=2n-1
Усі можливі стани атома водню класифікуються умовними позначеннями через позначення енергетичних оболонок n та їх підоболонок l за схемою, поданою в таблиці. Випромінювання та поглинання світла атомом відбувається з певними обмеженнями, які ще називають правилами відбору.
Виявляється, що при переходах електрона між енергетичними рівнями, у першому наближенні, повинно відбуватися таке обмеження на азимутальне квантове число l Dl=±1, (5) яке пов’язане із законом збереження імпульсу, коли враховані імпульси атома й фотона, що випромінюється чи поглинається. Таким чином в атомі можливі переходи nsÛmp, npÛmd і т.п.
б). Власні функції. Власні функції Наведемо декілька значень радіальної та сферичної функцій, поклавши
1. Для частинки у глибокій потенціальній ямі для енергії справджуються такі співвідношення
2. Для гармонічного осцилятора можна записати
3. Для воднеподібних атомів. У випадку n+1-го енергетичного рівня маємо
а відносний проміжок становитиме
В усіх перелічених випадках при великих числах n (n>>1) маємо Одержаний результат є окремим випадком загального принципу відповідності Бора, який він установив в 1923 році стосовно квантової механіки. За цим принципом будь-яка нова, більш узагальнена теорія природних явищ у фізиці, що є розвитком класичної теорії, не відкидає останньої узагалі, а містить її у собі у певних межах застосування, причому у граничних випадках нова теорія переходить у попередню. Так, наприклад, при малих швидкостях тіл V<<c, релятивістська механіка переходить у класичну, а при Принцип Паулі
При розгляді багатоелектронних систем виявляються їхні особливості, яких не мають багаточастинні системи в класичній теорії. Один із фундаментальних принципів багатоелектронної системи є принцип нерозрізнюваності тотожних частинок ¾ частинок, що мають однакові фізичні властивості (маса, заряд, спін і т.п.). Ці частинки повністю втрачають свою індивідуальність. Якщо позначити сукупність квантових характеристик для кожної з частинки, наприклад, для системи з двох частинок через х1 та х2, то їх y-функція має вигляд y(х1,х2). У зв’язку з нерозрізнюваністю частинок можна записати |y(х1,х2)|2=|y(х2,х1)|2, при цьому можливі два випадки · · Як показують розрахунки, до першого випадку відносяться частинки з цілим спіном S=0,1,2... і такі частинки називаються бозонами. Їх статистичні властивості дослідили Ш.Бозе та А.Ейнштейн. Згідно статистики, названої їх іменами (статистика Бозе-Ейнштейна), в межах системи таких частинок у кожному з можливих станів може знаходитися необмежене число частинок. До другого випадку відносяться частинки з напівцілим спіном В багатоелектронних атомах взаємодія електронів із ядром носить складний характер і розрахунок їх станів в атомі дещо ускладнюється. Проте наближено їх стани можна характеризувати чотирма квантовими числами, так як це зроблено для атома водню. На підставі дослідних даних, ще до створення квантової теорії, в 1925 році В.Паулі сформулював закон, названий принципом Паулі. Згідно цього закону в будь-якому атомі не може бути два електрони, що знаходяться в одному стаціонарному стані, який визначається набором чотирьох квантових чисел: головного ¾ n, орбітального ¾ l, магнітного ¾ m, спінового ¾ ms. Класифікація станів багатоелектронних атомів відповідає класифікації станів атома водню, а електрони у стаціонарному стані атома наповнюють стани відповідно до значень квантових чисел.
Молекулярні спектри
Молекула являє собою найменшу частинку речовини і складається з багатьох однакових чи різних атомів. Хімічні властивості молекул визначаються взаємодією зовнішніх електронів атомів, які називаються валентними електронами. Найпростішими молекулами є двоатомні з гомеополярним зв'язком: де І ¾ момент інерції молекули, М ¾ момент імпульсу, J ¾ квантове число момента імпульсу і
Запишемо тепер повну енергію Е у вигляді
· DL=±1 для електронних рівнів (L ¾ орбітальне квантове число), · · DJ=±1 для обертових рівнів.
Люмінесценція
Випромінювання, надмірне над тепловим, тривалість якого · при бомбардуванні тіл швидкими електронами та іншими, розігнаними до певних енергій, частинками, · пропусканні електричного струму ¾ ударна фотолюмінісценція, · дії достатньої величини напруженості електричного поля (електричний розряд) ¾ електролюмінісценція, · опроміненні іншим випромінюванням ¾фотолюмінісценція · при протіканні деяких хімічних реакцій ¾ хемілюмінесценція з частинним випадком біологічних перетворень (наприклад, гниття дерева) ¾ біолюмінесценція. При всіх названих джерелах виникнення люмінесценції, відбувається перехід атомів або іонів речовини у збуджений стан із наступним переходом їх в основний. При цьому може виникати люмінесцентне випромінювання електромагнітних хвиль. Поряд із цим можуть відбуватися і безвипромінювальні переходи. В залежності від тривалості люмінесцентного випромінювання t, люмінесценцію розділяють на · флуоресценцію (t ~ 10-8c ¸ 10-9c) ¾ фотолюмінісценція рідин та газів, та · фосфоресценцію, коли атоми тіла мають метастабільні збуджені рівні (10-4c >t> 10-8c). Для фотолюмінісценції встановлено правило: при фотолюмінісценції під дією видимого та рентгенівського випромінювання тіло випромінює світло на частотах ns менших частоти збуджуючого випромінювання nо ¾ стоксове випромінювання й випромінювання малої інтенсивності на частоті nаs більшій ніж частота збуджуючого випромінювання ¾ антистоксове випромінювання. Це правило віддзеркалює той факт, що при утворенні фотона з ns, частина енергії W кванта hno йде на неоптичні процеси, а в другому випадку до енергії джерела hno долучається енергія теплового руху атомів, величина якої пропорційна kT. Сфери застосування · створення економічних джерел освітлення (натрієві ¾ жовта лінія, ртутні ¾ жовта, зелена, синя та фіолетова лінії); · люмінесцентний аналіз для виявлення речовин із відносною масовою концентрацією до 10-11. · Комбінаційне розсіювання
Комбінаційне розсіювання(КР) ¾ модульоване розсіювання падаючого випромінювання молекулами речовини. В елементарному акті комбінаційного розсіювання відбувається поглинання молекулою падаючого кванта
де k – коефіцієнт, що визначає глибину модуляції (
З рівняння (2) видно, що на виході з речовини може бути додаткове електромагнітне випромінювання на частотах комбінаційного розсіювання Уперше мазер у сантиметровому діапазоні був створений у 1953 році Басовим та Прохоровим і незалежно від них Таунсом. В 1960 році Мейман (США) створив перший твердотільний лазер.
Розглянемо докладніше установки вимушеного випромінювання. 1. Рубіновий лазер утворюється кристалом рубіна, що є оксидом алюмінію Al2O3 із домішкою оксиду хрому Сr2O3 у кількості від 0.03% до 0.05%. Певна частина атомів Al у решітці рубіна заміщена атомами Cr3+, які утворюють активне середовище. Верхній енергетичний рівень А утворюється двома широкими енергетичними смугами, а метастабільний рівень В утворюється двома близькими рівнями, що відповідають довжинам хвиль червоного світла 692,7 нм та 694,3 нм (див.Мал.210). Накачка відбувається зеленим світлом потужної імпульсної лампи, наповненої неоном та криптоном. 2. Гелій-неоновий лазер. Активним середовищем є плазма високочастотного газового розряду в суміші гелію з неоном. Рівнем С є рівень збудження гелію близький до метастабільного рівня неону, який є рівнем системи В (див.Мал.211). Рівнем А є один із нижніх рівнів неону й перехід атомів неону зі збудженого стану В на цей нижній дає лазерне випромінювання з довжиною хвилі 632,8 нм.
· Часова когерентність складає t=10-3 с, довжина когерентності l=105 м (звичайні джерела світла мають t~10-8 c, l=3 м). · Монохроматичність, що вимірюється півшириною хвилі, складає Dl~10-11 м. · Надзвичайно велика потужність випромінювання. Нехай активне середовище одержало енергію 20 Дж і висвітлило цю енергію за 10-3 с, тобто створило потік eнергії Ф=2×104 Вт. Якщо сфокусувати це світло збірною лінзою на площу 1мм2=10-6 м2, то потік енергії на одиницю площі складе 2×1010 Вт/м2 ¾ 20 гігават на 1м2. · Кутова розбіжність лазерного випромінювання така, що промінь лазера створює на Місяці пляму діаметром до 3 км, коли звичайний прожектор дасть пляму діаметром до 40 000 км. · ККД лазерів за своїм типом може складати від 0,01% до 75%. Типи лазерів. · твердотільні, · газові, · напівпровідникові, · хімічні. Застосування лазерів · обробка та мікрозварювання твердих та надтвердих матеріалів, · дефектоскопія виробів, · хірургічний інструмент, · вимірювальна техніка, · створення голографічної пам’яті з високою швидкістю зчитування.
19.23.Контрольні питання 1. Розкажіть про дослід Девідсона-Джермера та застосуйте формулу Вульфа-Брега до розсіювання електронів. 2. Розгляньте явище дифракції електронів на отворах. 3. Знайдіть невизначеність імпульсу електрона, що дифрагує на щілині.. 4. Наведіть співвідношення невизначеностей та їх фізичний зміст. 5. Розкажіть про дослід Франка-Герца. 6. Опишіть борівську теорію атома водню. 7. Дайте визначення хвильової функції та розкажіть про її фізичний зміст. 8. Суперпозиція станів у квантовій механіці. 9. Розгляньте загальне та стаціонарне рівняння Шредінгера. 10. Розв'яжіть рівняння Шредінгера для вільної частинки. 11. Розв'яжіть рівняння Шредінгера для частинки у потенціальній ямі. 12. Що являє гармонічний осцилятор. Які частоти він випромінює. 13. Потенціальний бар'єр та його прозорість. 14. Запишіть рівняння Шредінгера для частинки у сферично симетричному потенціальному полі. 15. Псі-функція, квантові числа, рівні енергії та момент імпульсу воднеподібних атомів. 16. Розкажіть про квантування моменту імпульса атома. 17. Просторовий розподіл енергетичних рівнів в атомі водню. 18. Мезоатоми та ширини енергетичних рівнів. 19. Розкажіть про дослід Штерна-Герлаха. 20. Що являє спін електрона? 21. Принцип Паулі та розрахунок числа енергетичних рівнів в атомі та їх позначення. 22. Які основні положення формулюють періодичну систему хімічних елементів. 23. Що являють рентгенівські спектри випромінювання? 24. У чому полягає зміст закона Мозлі? 25. Яка фізична природа зв'язку атомів у молекулі водню? 26. Чим визначається енергія зв'язку двоатомних молекул? 27. Розкажіть про електронні, коливальні та обертальні терми молекул та яка їх структура. 28. Як утворюються молекулярні спектри. 29. Розкажіть про сутність люмінісценції та які види її існують? 30. Що приводить до комбінаційного розсіювання? 31. Які складові комбінаційного розсіювання та люмінісценції існують? 32. У чому полягає явище вимушеного випромінювання? 33. Яка передумова для заселеності атомних рівнів речовини призводить до лазерного випромінювання. 34. Наведіть принципову схему рубінового лазера, які довжини хвиль він випромінює? 35. Наведіть принципову схему гелій-неонового лазера. Які довжини хвиль він випромінює?
Елементи атомної фізики та квантової механіки.
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.01 с.) |

 . Для характеристики хвиль де Бройля знайдемо спочатку фазову
. Для характеристики хвиль де Бройля знайдемо спочатку фазову  та групову
та групову  швидкості такого хвильового процесу, у якому частинка рухається із швидкістю V<c і має енергію W. Для знаходження фазової швидкості, запишемо послідовність очевидних рівностей, що випливають з формули Луї де Бройля
швидкості такого хвильового процесу, у якому частинка рухається із швидкістю V<c і має енергію W. Для знаходження фазової швидкості, запишемо послідовність очевидних рівностей, що випливають з формули Луї де Бройля
 . Для групової швидкості маємо
. Для групової швидкості маємо
 ,
,  ,
, .
. .
. .
. .
. , яке він одержав в 1926 році. Це рівняння, як і рівняння руху Ньютона, не виводиться, а постулюється. Хвильове рівняння Шредінгера
, яке він одержав в 1926 році. Це рівняння, як і рівняння руху Ньютона, не виводиться, а постулюється. Хвильове рівняння Шредінгера (1)
(1) через потенціальну енергію силового поля U(x,y,z,t), в якому знаходиться частинка. В цьому рівнянні m ¾ маса частинки,
через потенціальну енергію силового поля U(x,y,z,t), в якому знаходиться частинка. В цьому рівнянні m ¾ маса частинки,  ¾ уявна одиниця,
¾ уявна одиниця,
 є скінченною величиною.
є скінченною величиною. функцію можна шукати у вигляді
функцію можна шукати у вигляді , (2)
, (2) , (3)
, (3) ;
; , (1)
, (1) ¾ хвильове число. Розв’язком цього рівняння є хвильова функція
¾ хвильове число. Розв’язком цього рівняння є хвильова функція . (2)
. (2) , (3)
, (3) . Таким чином рух вільної частинки у квантовій механіці описується плоскою монохроматичною хвилею. При розповсюдженні частинки в напрямкові Ох
. Таким чином рух вільної частинки у квантовій механіці описується плоскою монохроматичною хвилею. При розповсюдженні частинки в напрямкові Ох ,
, Гармонічним осцилятором називають частинку, що здійснює гармонічні коливання під дією пружної сили
Гармонічним осцилятором називають частинку, що здійснює гармонічні коливання під дією пружної сили  , де k¾ коефіцієнт пружності. Потенціальна енергія осцилятора
, де k¾ коефіцієнт пружності. Потенціальна енергія осцилятора 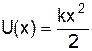 (див.Мал.196), а власна частота
(див.Мал.196), а власна частота 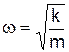 , де m ¾ маса частинки, тобто
, де m ¾ маса частинки, тобто .
. .
. .
. , називають нульовою енергією осцилятора і вона визначає його енергію при температурі Т=0 К, тобто при Т=0 К частинки, що знаходяться у вузлах кристалічної решітки здійснюють нульові коливання. Результати дослідів по розсіюванню світла в кристалах при ТÞ0 підтверджують цю тезу.
, називають нульовою енергією осцилятора і вона визначає його енергію при температурі Т=0 К, тобто при Т=0 К частинки, що знаходяться у вузлах кристалічної решітки здійснюють нульові коливання. Результати дослідів по розсіюванню світла в кристалах при ТÞ0 підтверджують цю тезу. , двічі іонізований атом літію
, двічі іонізований атом літію  і т.п. Потенціальна енергія електрона у таких атомах у полі ядра із зарядом Ze записується у вигляді
і т.п. Потенціальна енергія електрона у таких атомах у полі ядра із зарядом Ze записується у вигляді ,
, . (1)
. (1) . (2)
. (2) у сферичній системі координат, вкажемо, що розв’язок рівняння (2) знаходиться у вигляді
у сферичній системі координат, вкажемо, що розв’язок рівняння (2) знаходиться у вигляді (3)
(3) ¾ радіальна хвильова функція,
¾ радіальна хвильова функція,  ¾ сферична хвильова функція. Числа n,l,m мають назву квантових чисел:
¾ сферична хвильова функція. Числа n,l,m мають назву квантових чисел: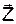 , яку ототожнюють із напрямком вектора магнітної індукції
, яку ототожнюють із напрямком вектора магнітної індукції  зовнішнього електромагнітного поля.
зовнішнього електромагнітного поля. , (1)
, (1) буде при n=1 і
буде при n=1 і (2)
(2) . (3)
. (3) (4)
(4)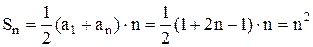 .
.
 є добутком двох множників
є добутком двох множників  . Множник
. Множник  є розв¢язком радіальної частини рівняння Шредінгера, ядром якого є функція Лагерра. Цей множник залежить від квантових чисел n, l. Сферична функція
є розв¢язком радіальної частини рівняння Шредінгера, ядром якого є функція Лагерра. Цей множник залежить від квантових чисел n, l. Сферична функція  є розв¢язком частини рівняння Шредінгера, яка залежить від кутів
є розв¢язком частини рівняння Шредінгера, яка залежить від кутів  і визначається квантовими числами l, m. Можна показати, що функція
і визначається квантовими числами l, m. Можна показати, що функція  і його проекції
і його проекції 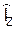 . Густина ймовірності знаходження електрона на відстані r від ядра задається виразом
. Густина ймовірності знаходження електрона на відстані r від ядра задається виразом  і для декількох функцій на малюнку 13 наведена відповідна її залежність від r у мірилі борівського радіуса
і для декількох функцій на малюнку 13 наведена відповідна її залежність від r у мірилі борівського радіуса  . З малюнка видно, що найбільш імовірними є відстані від ядра, що співпадають із радіусами відповідних борівських орбіт.
. З малюнка видно, що найбільш імовірними є відстані від ядра, що співпадають із радіусами відповідних борівських орбіт. (див.Мал.199)
(див.Мал.199) ,
,  ,
, .
. ,
,  ,
,  ,
,  .
. в). Принцип відповідності Бора. Розглянемо одну спільну властивість енергій електрона, що знаходиться у потенціальній ямі, електрона, що здійснює гармонічні коливання (осцилятор) та, на кінець, електрона у воднеподібному атомі. Знайдемо відносні проміжки енергій електронів для перелічених випадків.
в). Принцип відповідності Бора. Розглянемо одну спільну властивість енергій електрона, що знаходиться у потенціальній ямі, електрона, що здійснює гармонічні коливання (осцилятор) та, на кінець, електрона у воднеподібному атомі. Знайдемо відносні проміжки енергій електронів для перелічених випадків. ,
,  ,
,  .
. ,
,  ,
, 
 ,
, .
. й енергія стає неперервною. Це означає, що починаючи з деяких значень квантових чисел, енергія частинки може розглядатися як класична.
й енергія стає неперервною. Це означає, що починаючи з деяких значень квантових чисел, енергія частинки може розглядатися як класична. квантова механіка переходить у класичну.
квантова механіка переходить у класичну. ¾ y-функція, яка симетрична відносно перестановки частинок місцями;
¾ y-функція, яка симетрична відносно перестановки частинок місцями; ¾ y-функція, яка антисиметрична відносно перестановки частинок місцями.
¾ y-функція, яка антисиметрична відносно перестановки частинок місцями. і вони називаються ферміонами. Їх статистику досліджували Е.Фермі та П.Дірак. Згідно статистики, названої їх іменами (статистика Фермі-Дірака), в межах системи таких частинок у кожному з можливих станів може знаходитися лише одна частинка.
і вони називаються ферміонами. Їх статистику досліджували Е.Фермі та П.Дірак. Згідно статистики, названої їх іменами (статистика Фермі-Дірака), в межах системи таких частинок у кожному з можливих станів може знаходитися лише одна частинка. а також молекули з гетерополярним зв¢язком:
а також молекули з гетерополярним зв¢язком:  . У 1927 році Гайтлер та Лондон розв'язали рівняння Шредінгера для двоатомної молекули водню. У результаті було виявлено, що енергія молекули залежить від відстані r між молекулами та напрямками їх спінів. Для
. У 1927 році Гайтлер та Лондон розв'язали рівняння Шредінгера для двоатомної молекули водню. У результаті було виявлено, що енергія молекули залежить від відстані r між молекулами та напрямками їх спінів. Для 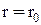 молекула має мінімум енергії, а в околиці
молекула має мінімум енергії, а в околиці 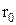 вона здійснює гармонічні коливання (див.Мал.205). На
вона здійснює гармонічні коливання (див.Мал.205). На 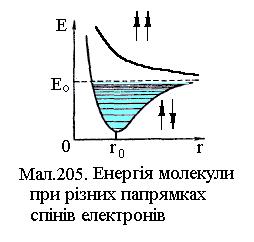 малюнку представлена залежність енергії молекули водню від відстані між атомами в основному стані для випадку паралельних та антипаралельних спінів електронів. У першому випадку молекула є стійким утворенням, а у другому випадку енергія не має мінімуму й молекула не може бути утворена взагалі. При електронному збудженні енергія молекули змінює криву залежності електронної енергії від відстані між атомами r, як це показано на малюнку. При заданій електронній конфігурації молекула може здійснювати коливальний та обертовий рух, які визначаються відповідними енергіями. Будова молекул та їх властивості виявляються з молекулярних спектрів, які утворюються електронними, коливальними та обертовими збудженнями атомів. Крім названих складових також розрізнюють електронно-коливальні (не змінюється коливальне квантове число v) та коливально-обертові (не змінюється обертове квантове число, яким є квантове число імпульсу J). Типові молекулярні спектри¾ смугасті, що представляються сукупністю вузьких смуг в інфрачервоній, видимій та ультрафіолетовій областях. Чим більше атомів у молекулі, тим складніший її спектр випромінювання. Розглянемо докладніше енергетичні стани молекул. Повна енергія молекули Е є сумою енергії Ее електронної конфігурації, енергій коливального ¾ Еv та енергії обертового руху ¾ Еr, причому
малюнку представлена залежність енергії молекули водню від відстані між атомами в основному стані для випадку паралельних та антипаралельних спінів електронів. У першому випадку молекула є стійким утворенням, а у другому випадку енергія не має мінімуму й молекула не може бути утворена взагалі. При електронному збудженні енергія молекули змінює криву залежності електронної енергії від відстані між атомами r, як це показано на малюнку. При заданій електронній конфігурації молекула може здійснювати коливальний та обертовий рух, які визначаються відповідними енергіями. Будова молекул та їх властивості виявляються з молекулярних спектрів, які утворюються електронними, коливальними та обертовими збудженнями атомів. Крім названих складових також розрізнюють електронно-коливальні (не змінюється коливальне квантове число v) та коливально-обертові (не змінюється обертове квантове число, яким є квантове число імпульсу J). Типові молекулярні спектри¾ смугасті, що представляються сукупністю вузьких смуг в інфрачервоній, видимій та ультрафіолетовій областях. Чим більше атомів у молекулі, тим складніший її спектр випромінювання. Розглянемо докладніше енергетичні стани молекул. Повна енергія молекули Е є сумою енергії Ее електронної конфігурації, енергій коливального ¾ Еv та енергії обертового руху ¾ Еr, причому 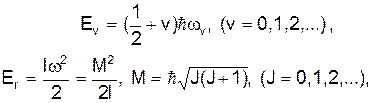 (1)
(1) . (2)
. (2)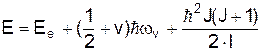 . (3)
. (3) Принципова схема енергетичних рівнів молекули показана на Мал.206.
Принципова схема енергетичних рівнів молекули показана на Мал.206. Закономірність переходу між енергетичними рівнями (3) молекули задається правилами відбору
Закономірність переходу між енергетичними рівнями (3) молекули задається правилами відбору для коливальних рівнів (v ¾ коливальне квантове число),
для коливальних рівнів (v ¾ коливальне квантове число), На відміну від лінійчатих спектрів випромінювання атомів молекулярні спектри складаються зі смуг, кожна з яких складається з тісно розташованих ліній, структура яких показана на Мал.207. смуги молекулярного спектра азоту. З цієї причини молекулярні спектри мають назву смугастих. Розрізнюють три види смуг: обертові, коливально-обертові та електронно-коливальні. Останні мають різко виражений кант з одного боку, як згусток близько розташованих ліній, а з другого кінця край спектра є розмитим.
На відміну від лінійчатих спектрів випромінювання атомів молекулярні спектри складаються зі смуг, кожна з яких складається з тісно розташованих ліній, структура яких показана на Мал.207. смуги молекулярного спектра азоту. З цієї причини молекулярні спектри мають назву смугастих. Розрізнюють три види смуг: обертові, коливально-обертові та електронно-коливальні. Останні мають різко виражений кант з одного боку, як згусток близько розташованих ліній, а з другого кінця край спектра є розмитим. називається люмінесценцією. Таке випромінювання може народжуватися
називається люмінесценцією. Таке випромінювання може народжуватися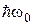 і наступного випромінювання кванта
і наступного випромінювання кванта  , де wкол ¾ одна з частот коливального спектра молекули. Квант
, де wкол ¾ одна з частот коливального спектра молекули. Квант 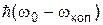 відповідає стоксовій лінії
відповідає стоксовій лінії  , а
, а  ¾ антистоксова лінія. Комбінаційне розсіювання є потужним методом для визначення частот коливального спектра молекул та якісного й кількісного аналізу складу речовини за характеристичними спектрами коливальних зв’язків між атомами в молекулах при достатньо малих концентраціях речовин. На Мал.208 показано спектр комбінаційного розсіювання кисню. Молекула кисню збуджувалась лінією ртуті на частоті
¾ антистоксова лінія. Комбінаційне розсіювання є потужним методом для визначення частот коливального спектра молекул та якісного й кількісного аналізу складу речовини за характеристичними спектрами коливальних зв’язків між атомами в молекулах при достатньо малих концентраціях речовин. На Мал.208 показано спектр комбінаційного розсіювання кисню. Молекула кисню збуджувалась лінією ртуті на частоті 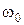 , яка відповідає довжині хвилі
, яка відповідає довжині хвилі 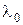 =253.7 нм. Симетрично частоті збудження розташовані стоксові та антистоксові лініїчастот
=253.7 нм. Симетрично частоті збудження розташовані стоксові та антистоксові лініїчастот  . 3
. 3 З класичної точки зору КР є результатом модуляції амплітуди зовнішнього електромагнітного випромінювання
З класичної точки зору КР є результатом модуляції амплітуди зовнішнього електромагнітного випромінювання 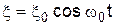 внутрішніми коливаннями атома
внутрішніми коливаннями атома 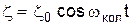 , тобто на виході з речовини електромагнітні коливання будуть описуватися рівнянням
, тобто на виході з речовини електромагнітні коливання будуть описуватися рівнянням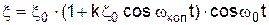 , (1)
, (1) ). Рівняння (1) може бути розкрите у вигляді
). Рівняння (1) може бути розкрите у вигляді . (2)
. (2) .
.
 Властивості лазерного випромінювання.
Властивості лазерного випромінювання.


