Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет момента инерции маятника ОбербекаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И момента сил сопротивления
Для расчета движения механической системы маятник–груз применим уравнение динамики поступательного движения для груза, закрепленного на нити, и уравнение динамики вращательного движения для маятника. Груз массой
Момент силы сопротивления относительно оси вращения Запишем для маятника основной закон динамики вращательного движения
где В скалярной форме это уравнение имеет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О,направление которой выбрано «от нас»)
Используя кинематическую связь линейного и углового ускоре- скорости
Решим систему уравнений (3.1) и (3.2), для чего умножим (3.1) на
Выражаем момент инерции маятника Обербека
Все величины, кроме Пусть J – момент инерции маятника Обербека без грузов. Из (3.4) следует, что
В условиях эксперимента Эту зависимость можно использовать для экспериментальной оценки величины
Для определения момента инерции маятника J воспользуемся (3.4), где величина
Для используемого в работе маятника Обербека справедливо неравенство
Для расчетов удобно представить момент инерции в виде
где Для определения момента инерции маятника необходимо измерить время
Зависимость момента инерции маятника от расстояния грузов до оси вращения Момент инерции маятника Обербека может быть представлен как сумма моментов инерции барабана со стержнями (
Эту зависимость момента инерции от расстояния грузов до оси вращения предполагается проверить, используя результаты опытов, полученные по формуле (3.7). Значение
Задание к работе 1. Приступив к работе, снимите грузы 2. Заранее выберите отметку (например, от 30 до 50 см), от которой начнется движение груза 3. Вращая маятник рукой, намотайте нить на шкив большего диаметра. Следите, чтобы груз 4. Включите электронный секундомер. 5. Проведите первый опыт, используя в качестве груза, тянущего нить, только одну подставку массой 6. Проведите по одному опыту, поместив на подставку сначала один, а затем сразу два подгрузка. Результаты внесите в таблицу измерений. По формуле (3.3) рассчитайте величину углового ускорения 7. Постройте зависимость e(m). Определите из графика по точке его пересечения с осью абсцисс значение m 0, при котором e = 0. Рассчитайте по формуле (3.6) величину момента сил сопротивления 8. Проведите прямые пятикратные измерения времени опускания груза для заданного расстояния x. 9. Рассчитайте среднее время t и определите доверительную по-грешность измерения 10. Вычислите по формуле (3.7) среднее значение момента инерции барабана со стержнями 11. Определите доверительную погрешность косвенных измерений этого момента инерции 12. Закрепив грузы m 1 на стержнях маятника на равном расстоянии r от оси вращения, определите это расстояние, учитывая деления, нанесенные на стержни, и указанные около установки и в Приложении исходные данные. 13. Проведите однократные измерения времени 14. Вычислите моменты инерции маятника с грузами на стержнях по формуле (3.7) при различных расстояниях r. При этом, как показали предварительные опыты, можно с допустимой точностью использовать в качестве величины m 0 ее значение, найденное ранее для крестовины без грузов на спицах. Сравните полученные данные со значениями момента инерции, вычисленными по формуле (3.8) для соответствующих значений r. Результаты вычислений занесите в таблицу измерений. 15. Постройте на одном рисунке графики экспериментально полученной и теоретически ожидаемой зависимости момента инерции маятника от
Контрольные вопросы 1. Какова цель данной работы? 2. Что такое момент инерции? Каков его физический смысл. 3. Как можно изменить момент инерции маятника Обербека? 4. Как из уравнений динамики поступательного и вращательного движений вывести рабочую формулу (3.7)? 5. В каком случае движение маятника является равноускоренным? 6. Как измерить расстояние от оси вращения до центров грузиков, закрепленных на стержнях? 7. Каким образом в данной работе подтверждается линейная за- Индивидуальные задания для членов бригады, выполняющих лабораторную работу на одной установке
Литература
Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т. 1 (и последующие издания этого курса).
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
Цели работы: 1) оценить момент тормозящей силы, действующий на тело в процессе вращения; 2) определить момент инерции тела с учетом момента тормозящей силы; 3) произвести расчет моментов, пользуясь энергетическими соотношениями. Описание установки
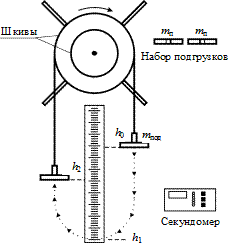
Установка представляет собой тело со шкивом радиусом r, которое вращается в шарикоподшипниках. На шкив намотана нить, один конец которой прикреплен к шкиву, а другой – к подставке массой
Рис. 4.1
В процессе движения часть механической энергии системы тело–груз расходуется на работу против тормозящей силы и, следовательно, превращается во внутреннюю энергию системы и окружающего воздуха, которые нагреваются. Из этого следует, что тело поднимет груз на высоту, меньшую начальной, т. е. отметка h 2 всегда будет расположена ниже отметки h 0. Тормозящая сила складывается из силы трения в подшипниках и из силы трения о воздух при движении тела и груза.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.138.214 (0.008 с.) |

 движется с ускорением
движется с ускорением 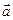 под действием результирующей сил тяжести
под действием результирующей сил тяжести 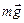 и силы натяжения нити
и силы натяжения нити 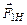 (рис. 3.2). Запишем для груза второй закон Ньютона в проекции на направление движения
(рис. 3.2). Запишем для груза второй закон Ньютона в проекции на направление движения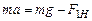 (3.1)
(3.1)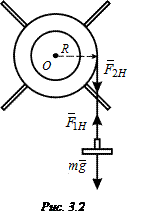 Сила натяжения передается нитью от груза к шкиву вращающегося маятника. Если предположить, что нить невесомая, то на шкив маятника действует сила
Сила натяжения передается нитью от груза к шкиву вращающегося маятника. Если предположить, что нить невесомая, то на шкив маятника действует сила 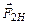 , равная по величине
, равная по величине 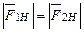 ). Сила натяжения создает вращательный момент
). Сила натяжения создает вращательный момент 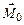 относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина этого момента равна
относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина этого момента равна 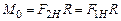 , где
, где 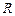 – радиус шкива, на который намотана нить,
– радиус шкива, на который намотана нить,  , где
, где 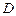 – диаметр шкива.
– диаметр шкива.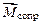 направлен «к нам», т. е. в противоположную по отношению к вращательному моменту сторону.
направлен «к нам», т. е. в противоположную по отношению к вращательному моменту сторону.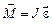 ,
, – результирующий момент сил;
– результирующий момент сил; 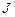 – момент инерции маятника;
– момент инерции маятника;  – угловое ускорение.
– угловое ускорение. . (3.2)
. (3.2)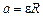 , а также уравнение движения груза при нулевой начальной
, а также уравнение движения груза при нулевой начальной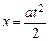 , выразим
, выразим 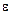 через измеряемые величины
через измеряемые величины  и
и 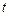
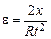 . (3.3)
. (3.3)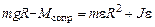 .
.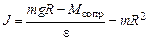 . (3.4)
. (3.4) , входящие в это уравнение, известны. Поставим задачу экспериментального определения
, входящие в это уравнение, известны. Поставим задачу экспериментального определения 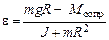 . (3.5)
. (3.5)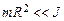 , что позволяет считать зависимость e(m)линейной.
, что позволяет считать зависимость e(m)линейной.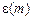 экстраполировать до пересечения с осью абсцисс, т. е. до точки
экстраполировать до пересечения с осью абсцисс, т. е. до точки 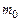 на этой оси, для которой выполняется (см. 3.5) равенство
на этой оси, для которой выполняется (см. 3.5) равенство  , то это позволит определить
, то это позволит определить 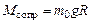 . (3.6)
. (3.6)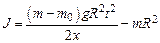 .
.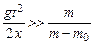 . Учитывая это, получаем
. Учитывая это, получаем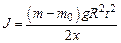 .
. , (3.7)
, (3.7)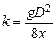 .
. ) и моментов инерции четырех грузов массой
) и моментов инерции четырех грузов массой 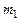 , закрепленных на расстояниях r от оси вращения (
, закрепленных на расстояниях r от оси вращения ( ). Если размеры этих грузиков малы по сравнению с
). Если размеры этих грузиков малы по сравнению с 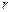 , то их можно считать материальными точками. Для материальной точки момент инерции равен
, то их можно считать материальными точками. Для материальной точки момент инерции равен 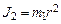 . Тогда момент инерции маятника
. Тогда момент инерции маятника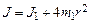 . (3.8)
. (3.8)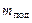 без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №1 (светится индикатор «Реж.1»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее маятник, и одновременно включится секундомер. При включенном режиме №1 секундомер в момент прохождения грузом нижней точки автоматически остановится, причем одновременно сработает тормозное устройство. Внесите результаты первого опыта в таблицу измерений.
без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №1 (светится индикатор «Реж.1»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее маятник, и одновременно включится секундомер. При включенном режиме №1 секундомер в момент прохождения грузом нижней точки автоматически остановится, причем одновременно сработает тормозное устройство. Внесите результаты первого опыта в таблицу измерений. при доверительной вероятности Р = 90 %,
при доверительной вероятности Р = 90 %, 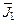 .
.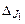 (см. Введение) и запишите результаты в виде
(см. Введение) и запишите результаты в виде 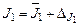 .
.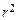 . Нанесите на график точки, соответствующие результатам, полученным при выполнении индивидуальных заданий. Проанализируйте возможные причины их несовпадения.
. Нанесите на график точки, соответствующие результатам, полученным при выполнении индивидуальных заданий. Проанализируйте возможные причины их несовпадения. . Груз под действием силы тяжести может опускаться, приводя во вращение тело. После того как груз от отметки h 0 опустится на полную длину нити до отметки h 1
. Груз под действием силы тяжести может опускаться, приводя во вращение тело. После того как груз от отметки h 0 опустится на полную длину нити до отметки h 1