Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод измерения показателя адиабатыСодержание книги
Поиск на нашем сайте
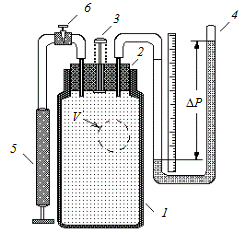
Технически более просто осуществляется адиабатный процесс расширения газа из равновесного состояния 1, при котором температура системы Т 1 равна температуре Т о окружающей внешней среды, Для эксперимента необходима система, способная спонтанно увеличить свой объем при неизменном количестве вещества в нем. Такая система не может быть ограничена стенками какого-либо сосуда, имеющего постоянный объем. В то же время избыточное давление в системе можно обеспечить только тогда, когда она заключена в таком сосуде. Для устранения этого противоречия выберем систему молекул внутри сосуда, но занимающую при избыточном давлении Р 1 только небольшую часть V 1 объема сосуда, как показано на рис. 6.1, где выделенная система условно ограничена круговой линией.
Рис. 6.1
В исходное равновесное состояние 1 система приходит после предварительного сжатия (подкачка газа может быть осуществлена насосом) и последующей релаксации (в течение нескольких минут), когда в условиях теплового равновесия с внешней средой весь газ в сосуде будет иметь температуру Т 1 = Т о и установившееся давление Р 1. В процессе быстрого адиабатного расширения системы, производимого резким соединением через открывающийся клапан К полости сосуда с внешней средой, теплообменом газа в сосуде и, тем более, в выделенной системе, можно пренебречь (d Q ® 0). Внутренняя энергия системы уменьшается на величину
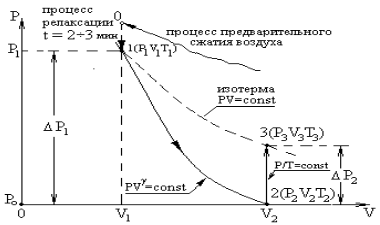
Рис. 6.2
Из уравнения (6.1) адиабатного процесса для состояний 1 и 2 следует равенство
В формуле (6.5)
так как
а отношение объемов V 2 / V 1 остается неизменным. Особенностъ метода Клемана и Дезорма состоит в том, что после адиабатного процесса из состояния 2 система, сохраняя постоянный объем, изохорически в течение некоторого времени переходит в равновесное состояние 3 (см. рис. 6.1), при котором в условиях теплового равновесия с внешней средой она приобретает температуру Т о этой среды: V 3 = V 2, Т 3 = Т о и Р 3 > Р 0. Таким образом, состояния 1 и 3 являются изотермическими (Т 1 = Т о и Т 3 = Т о), т. е. принадлежат некоторой теоретической изотерме (на рис. 6.2 – пунктирная линия РV = const). Поэтому для этих состояний можно записать равенство Р 1 V 1 = Р 3 V 3, либо, учитывая, что V 3 = V 2, равенство Р 1 V 1 = Р 3 V 2. Отсюда следует, что в формуле (6.3) неизвестное отношение объемов можно заменить отношением давлений
где
Подставив найденные выражения для логарифмов в формулу (6.5) запишем в окончательном виде уравнение, позволяющее производить измерение показателя адиабаты по методу Клемана и Дезорма,
Измерения с помощью формулы (6.6) – косвенные. Однако при обработке результатов измерений их следует рассматривать как прямые, в каждом эксперименте вычисляя значение g1, g2,…g i,…g n , а затем находя среднее значение Экспериментальная установка
Рис. 6.3
Установка, изображенная на рис. 6.3, содержит стеклянный со- 1) открыть вентиль 6; 2) насосом 5 малыми порциями накачать воздух в сосуд 1, создав давление, при котором в открытом колене манометра 4 уровень жидкости устанавливается вблизи верхнего деления шкалы. Следить, чтобы жидкость из трубки манометра не вылилась наружу; 3) закрыть вентиль 6; 4) в течение 2–3 мин дать системе придти в состояние равновесия (исходное состояние 1) при температуре внешней среды; измерить приращение давления D Р 1 по шкале манометра 4; 5) резким нажатием клапана 3 осуществить быстрое адиабатическое расширение системы; в момент выравнивания уровней жидкости в обоих коленах манометра клапан 3 отпустить; 6) в течение 2–3 мин осуществить изохорический процесс, по окончании которого система приходит в состояние 3 равновесия при температуре внешней среды, а давление Р 3 стабилизируется. Измерить приращение давления D Р 2 по шкале манометра 4; 7) с помощью формулы (6.6) вычислить значение показателя адиабаты.
Задание к работе
1. Тщательно изучить равновесные и квазиравновесные тепловые процессы, включая адиабатный процесс, а также понятие о степенях свободы молекул, вопросы теплоемкости идеальных газов, первое начало термодинамики. 2. Изучить метод Клемана и Дезорма, применяемый для измерения показателя адиабаты. 3. Провести 10–15-кратное измерение показателя адиабаты с помощью формулы (6.6), определяя приращения давления D Р 1 и D Р 2 и вычисляя g. 4. Вычислить среднее значение показателя адиабатыи, при доверительной вероятности Р = 90 %, случайную погрешность измерений, считая их прямыми (см. Введение). 5. Найти теоретическое значение показателя адиабаты для двухатомного газа и сравнить его с экспериментально полученным значением. Контрольные вопросы
1. Дайте определение термодинамически изолированной системы. 2. Какие состояния системы называют равновесными? 3. Что такое процесс релаксации системы, время релаксации системы? 4. Какие процессы называют равновесными и квазиравновесными? 5. Дайте определение всех изопроцессов и адиабатного процесса, напишите уравнения этих процессов, приведите их графическое изображение на диаграмме состояний. 6. Охарактеризуйте изопроцессы и адиабатный процесс с точки зренияих равновесности. 7. Что называют степенями свободы молекул и чему равно их число для одно-, двух- и трехатомных молекул? 8. Дайте определения теплоемкости, удельной и молярной теплоемкостей системы. Чему равны молярные теплоемкости идеального газа при изобарическом и изохорическом процессах? Как эти теплоемкости связаны друг с другом? 9. Изложите сущность метода Клемана и Дезорма для измерения показателя адиабаты. 10. Что называется показателем адиабаты, чем он определяетсяи как связан с теплоемкостями идеального газа при изобарическом и изохорическом процессах?
Литература
Савельев И.В. Курс общей физики. – М.: Наука, 1982. – T. 12
Приложение
Исходные данные для лаборатории,
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.221 (0.008 с.) |

 Р 1 превышает значение атмосферного давле-
Р 1 превышает значение атмосферного давле-
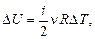 расходуемую на работу А расширения системы: D U ® А. На диаграмме (рис. 6.2) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически.
расходуемую на работу А расширения системы: D U ® А. На диаграмме (рис. 6.2) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически. , но так как Р 2 = Р о, то можно записать, что
, но так как Р 2 = Р о, то можно записать, что 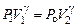 . Отсюда найдем, что показатель адиабаты
. Отсюда найдем, что показатель адиабаты . (6.5)
. (6.5)
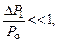
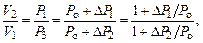
 – приращение давления при изохорическом процессе. Учитывая, что
– приращение давления при изохорическом процессе. Учитывая, что  и
и  получаем
получаем
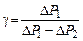 .
. и погрешность Dg. Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (Р 1, V 1, Т 1) системы, которое образуется спонтанно из неравновесного состояния 0, в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.
и погрешность Dg. Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (Р 1, V 1, Т 1) системы, которое образуется спонтанно из неравновесного состояния 0, в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.