
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В.2. Обработка и представление результатовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте МЕХАНИКА И ТЕРМОДИНАМИКА Методические указания к вводному занятию и к лабораторным работам № 0 – 6 по физике для студентов I курса всех факультетов
Новосибирск УДК 531+536] (076.5) М 55
Составители: А.В. Баранов (введение, лаб. работа № 0) А.М. Погорельский, В.В. Христофоров (лаб. работа № 1) Б.Л. Паклин (лаб. работа № 3) А.М. Погорельский, В.В. Христофоров (лаб. работа № 4) В.В. Христофоров (лаб. работа № 5 новая редакция) Д.Д. Березиков (лаб. работа № 6)
Разработка и изготовление лабораторных установок: А.М. Погорельский, А.В. Морозов, А.А. Шевченко, П.А. Крапивко
Подготовка к изданию: В.В. Христофоров
Рецензент: Б.И. Юдин
Работа подготовлена на кафедре общей физики
Ó Новосибирский государственный
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.......................................................................................................................... 4
Лабораторная работа № 0. ОПРЕДЕЛЕНИЕ ОБЪЕМА ТЕЛА ЦИЛИНДРИЧЕСКОЙ ФОРМЫ........................................................................ 26
Лабораторная работа № 1. ИЗМЕРЕНИЕ СКОРОСТИ ПУЛИ С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА................................ 30
Лабораторная работа № 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАЯТНИКА ОБЕРБЕКА.................................................................................. 38
Лабораторная работа № 4 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА.................................................................................................. 45
Лабораторная работа № 5. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА МЕТОДОМ КОЛЕБАНИЙ................................................................................ 58
Лабораторная работа № 6. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ МЕТОДОМ КЛЕМАНА И ДЕЗОРМА............................................................ 64
Введение
В лабораторном практикуме Вы постоянно будете иметь дело с измерениями физических величин. Необходимо уметь правильно обрабатывать и представлять результаты этих измерений. Цель данного раздела – сообщить основные сведения, касающиеся особенностей физических измерений, обработки и представления результатов. Для более полной и детальной информации следует обращаться к специальной литературе, например [1–5].
В.1. Погрешности измерений физических величин Под измерением понимается операция, в результате которой определяется, во сколько раз интересующая нас величина больше или меньше величины той же природы, принятой за единицу. Таким образом, измерение является актом сравнения: расстояние сравнивается с единицей расстояния, время – с единицей времени, ток – с единицей тока и т. д. Единицы измерения при этом должны быть предварительно определены. В лабораторном практикуме необходимо придерживаться международной системы единиц СИ. Часто одну и ту же величину можно измерить разными способами. Например, высоту здания можно измерить с помощью: 1) рулетки; 2) секундомера, определив время свободного падения небольшого по размерам металлического шарика; 3) рулетки, угломера и лазера, определив расстояние от здания 4) и т. д.
Анализируя подобные ситуации, можно прийти к следующему выводу. Измерения бывают прямыми и косвенными. В случае прямого измерения значение искомой величины непосредственно определяется с помощью прибора, шкала которого проградуирована в единицах измерения этой величины. В случае косвенного измерения значение величины вычисляется по формуле, которая связывает искомую величину с другими, измеренными прямо или косвенно. Очевидно, в нашем примере первое измерение высоты является прямым, а второе и третье – косвенными. Измерение можно проводить как однократно, так и многократно, пытаясь воспроизвести одни и те же условия. Если мы произведем многократные измерения высоты здания последовательно каждым из трех способов, то сравнение результатов измерений между собой приведет нас к очень интересным и важным выводам: 1. Результаты измерений первым способом могут отличаться от результатов измерений вторым способом, а последние, в свою очередь, от результатов измерений третьим способом и т. п. Разные способы измерения одной и той же величины могут давать разные ее значения. 2. Результаты многократных измерений с помощью одного и того же способа тоже могут отличаться друг от друга. Многократные измерения одной и той же величины одним и тем же способом могут дать разные ее значения. Проанализируем сложившуюся ситуацию. Сначала выясним, почему разные способы измерения одной и той же высоты привели к разным результатам. На первый взгляд, первый способ – самый надежный. Мы прикладываем ленту рулетки к поверхности здания и определяем искомую высоту. Более внимательный анализ показывает, что это не совсем так. Оказывается, здание построено с небольшим наклоном, а стена в том месте, где производятся замеры, имеет определенную кривизну – она выпуклая, причем в сторону улицы. Это означает, что мы измеряли не высоту здания, а длину стены, связанную с высотой. Второй способ представляет собой косвенное измерение. Измерив время падения шарика, мы рассчитываем высоту по известной формуле для свободного падения: h = gt 2/2. На этот раз измерение действительно касается высоты. Но мы забыли о том, что шарик движется в воз-духе и, следовательно, испытывает сопротивление среды. Поэтому рассчитанная по формуле величина также не является истинным значением высоты здания. Третье измерение, как и второе, является косвенным. Высота определяется из геометрических соображений: в прямоугольном треугольнике длина противолежащего катета равна произведению длины прилежащего катета на тангенс угла. В нашем случае высота играет роль одного катета, а расстояние от лазера до здания – роль другого. На этот раз нас подвело предположение об идеально горизонтальной поверхности, на которой стоит здание. Результат – опять измерена величина, не являющаяся высотой, но теперь по другой причине. Итак, в каждом способе измерения присутствуют какие-то постоянные факторы (в каждом случае свои, причем их может быть несколько), которые приводят к появлению систематической погрешности измерения данным способом. Каждый раз при измерении значения одной и той же величины в одних и тех же условиях систематическая погрешность имеет одно и то же значение. Если эти факторы учесть, введя соответствующие поправки, то можно приблизиться к реальному значению измеряемой величины, и тогда результаты измерений разными способами (с учетом поправок на систематическую погрешность) могут оказаться довольно близкими. Таким образом, Теперь попытаемся выяснить, почему многократные измерения одной и той же высоты одним и тем же способом (включая один и тот же комплект приборов) могут приводить к отличающимся друг от друга значениям. Это связано с целым рядом факторов, действующих случайным образом. В рассмотренном примере могут быть небольшие механические колебания почвы, здания и приборов, тепловые воздействия, связанные с изменением линейных размеров стены и используемых приборов, и т. п. Наконец, есть еще человеческий фактор, связанный с восприятием происходящих процессов и реакцией на это восприятие. В результате при повторных измерениях одной и той же величины могут получаться различные ее значения, связанные со случайными погрешностями. От измерения к измерению случайная погрешность может изменять как свой знак, так и свою величину. В силу случайного характера воздействий заранее предсказать величину такой погрешности невозможно. Наш анализ вызывает закономерные вопросы: 1. Что такое «истинное» значение измеряемой величины? 2. Как представлять результаты измерений с учетом погреш-ностей? Поскольку эти вопросы касаются не только рассмотренного примера, но и любых других измерений, мы перейдем к обобщениям и выработке общих рекомендаций. Приведенный конкретный пример продемонстрировал общее свойство, характерное для любых измерений, – любое измерение сопровождается погрешностями. Это свойство, в конечном счете, обусловлено тем, что всякое измерение предполагает определенную взаимосвязанную цепочку участников процедуры измерения: наблюдатель – измерительный прибор – анализируемый объект – «внешняя среда». Элементы этой цепочки связаны огромным количеством взаимодействий и движений. В процессе измерения анализируемый объект, измерительный прибор и наблюдатель могут быть подвержены различным влияниям (в том числе и взаимным), что и сказывается на результате измерений. Безусловно, если уменьшать влияния, не имеющие непосредственного отношения к процедуре измерения, и стараться учитывать неустранимые влияния, то точность наших измерений будет возрастать. Но абсолютно точное измерение невозможно принципиально. И это во многом связано с природой самих измеряемых величин. Если мы, например, захотим абсолютно точно измерить длину металлического стержня, то обнаружим наличие принципиально неустранимых (хотя и очень малых) колебаний кристаллической решетки. Никакой абсолютно точной «истинной» длины у стержня нет. Она постоянно случайным образом изменяется, отклоняясь в ту или иную сторону от некоторого наиболее часто встречающегося значения. Вот это значение мы можем принять за «истинное» значение длины и в дальнейшем оперировать именно им, говоря о длине стержня, или используя эту величину для каких-либо расчетов, например для определения объема стержня. Такого рода ситуация обнаруживается во множестве других измерений. Сами измеряемые величины случайным образом могут изменяться, что обусловлено, как уже сказано выше, физической природой этих величин. Таким образом, мы сталкиваемся с принципиальной неустранимостью случайных факторов. Их можно свести к минимуму, но окончательно избавиться от них нельзя. Следовательно, представляя результаты измерений, мы должны давать информацию, касающуюся нашей оценки «истинного» значения величины
Многократных измерений
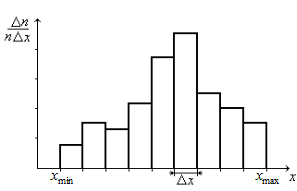
Допустим, что мы n раз измерили значение некоторой величины x. Вследствие случайных факторов получается совокупность n различных значений одной и той же величины x. Эта совокупность значений получила название конечной выборки. Пусть максимальное измеренное значение равно x max, минимальное – x min. Представим результаты измерений в графической форме. Для этого предварительно проведем некоторую их обработку. Разобьем полный интервал изменения величины x на m более мелких интервалов и введем величину интервала
Рис. В.1. Гистограмма результатов измерений величины x График представляет собой столбчатую диаграмму, которая называется гистограммой. Гистограмма достаточно наглядно демонстрирует, как распределены значения результатов измерений: одни значения величины x в процессе измерений получались довольно редко, другие – более часто, а какие-то – очень часто. На некоторый интервал D x приходится максимальное значение величины y. Из опыта следует, что при увеличении числа измерений гистограмма будет принимать простую и вполне определенную форму, которая для множества различных экспериментов оказывается универсальной. Если совершить предельный переход: n ® ¥, D x ® 0, то гистограмма превратится в непрерывную кривую, которая описывает функция следующего вида:
f (x) = A exp{–(x – x 0) 2 / 2s 2}. (В.1)
Эта зависимость получила название функции распределения Гаусса, или закона нормального распределения Гаусса. Ее график изображен на рис. В.2. Изображенная непрерывная кривая является, таким образом, предельным, или, как его еще называют, генеральным распределением.
Рис. В.2. Функция распределения Гаусса
Предельное распределение – это теоретическая идеализация, к которой никогда нельзя абсолютно точно приблизиться в эксперименте. Чем больше количество измерений, тем ближе гистограмма к предельному распределению. Теоретическая идеализация, хотя и недостижима, очень важна: она демонстрирует предельные возможности распределения результатов в данном эксперименте. Если бы могли получить в эксперименте предельное распределение, то информация, содержащаяся в нем, была максимально возможной и полной. Следует подчеркнуть, что не все предельные распределения имеют вид нормального распределения Гаусса. Но такое распределение чаще всего будет соответствовать Вашим экспериментальным данным. По этой причине мы рассматриваем именно это распределение. Возможно, в дальнейшем Вы познакомитесь и с другими распределениями. Нормальное (генеральное) распределение характеризуется двумя параметрами: 1) генеральным средним значением x 0; 2) генеральным отклонением s. Генеральное среднее представляет собой то значение x, на которое приходится максимум функции распределения Гаусса. Значения случайной величины x распределены относительно x 0симметрично (кривая нормального распределения имеет ось симметрии, проходящую через координату x 0). Генеральное отклонение представляет собой меру ширины кривой нормального распределения. Чем меньше значение s, тем быстрее уменьшается значение функции Гаусса по мере удаления значения x от величины генерального среднего, тем уже кривая нормального распределения, меньше разброс значений измеряемой величины и, следовательно, точнее измерение. Функция распределения Гаусса позволяет рассчитать долю из-
где x 1 – нижняя граница выбранного интервала значений величины х; Функция распределения Гаусса (В.1) удовлетворяет условию нормировки:
Поэтому (В.2) можно интерпретировать как вероятность P того, что «истинное» значение измеряемой величины окажется в интересующем нас интервале. Из геометрического смысла интеграла следует, что площадь под кривой нормального распределения в пределах выбранного интервала (см. рис. В.2), отнесенная к полной площади под всей кривой, должна давать величину этой вероятности и, соответственно, значение Δ n / n. Используя вероятностный смысл функции Гаусса, можно показать, что среднее значение измеряемой величины, определяемое как
в случае нормального распределения совпадает с x 0, т. е. Аналогично можно показать, что значение sсовпадает с величиной стандартного, или среднеквадратичного, отклонения, квадрат которого для нормального распределения определяется выражением Возьмем интервал (x 0– Δ x, x 0+ Δ x), границы которого симметричны по отношению к генеральному среднему. Пользуясь (В.2), для нормального распределения можно определить вероятность P попадания «истинного» значения измеряемой величины в этот интервал. Если вероятность определена, то интервал называется доверительным интервалом измерения, а вероятность – доверительной вероятностью, или надежностью измерения. Надежность измерения выражается или в долях единицы или в процентах и зависит от величины выбранного интервала. Если задан доверительный интервал с указанием величины надежности (вероятности P), то информация о результатах измерения считается представленной с учетом случайных погрешностей измерения. Величина Δ x, характеризующая ширину доверительного интервала, называется доверительной погрешностью. В качестве доверительного интервала для нормального распределения чаще всего используется интервал (x 0– s, x 0+ s), связанный со стандартным отклонением. Величина доверительной вероятности для такого интервала составляет приблизительно 68,3 %. Если взять Δ x = 2s, то P = 95,5 %. При Δ x = 3s величина P = 99,7 %. Последнее, например, означает, что вероятность обнаружить результат измерения величины x за пределами интервала (x 0 – 3s, x 0 + 3s) составляет всего 0,3 %. Можно считать, что «истинное» значение измеряемой величины практически находится в этом интервале. От функции распределения Гаусса, которая является теоретической предельной идеализацией, вернемся теперь к нашему реальному распределению (см. рис. В.1), в котором количество измерений n представляет собой конечную величину. Как в этом случае определяется доверительный интервал и представляются результаты измерений? Аналогом величины x 0выступает величина выборочного среднего значения (среднеарифметического для конечной выборки)
Аналогом величины sявляется величина выборочного среднеквадратичного отклонения
S x =
Чтобы получить оценку доверительного интервала для конечного числа измерений, приходится вводить величину t S – коэффициент Стьюдента (псевдоним английского математика В.С. Госсета). Только введение этого коэффициента позволяет найти доверительную вероятность для заданного интервала значений или определить интервал для заданной величины вероятности. Последняя из этих двух операций более простая, поэтому мы будем поступать именно так. Значения коэффициента Стьюдента для различных значений n и P даны
Т а б л и ц а В.1
В.3. Приборная погрешность В настоящее время существует огромное количество разнообразных измерительных приборов, отличающихся конструкцией, принципом работы и точностью. Точность прибора либо задается классом точности, либо указывается в паспорте, прилагаемом к прибору Измерительные приборы вносят свой вклад в погрешность измерения, зависящий от точности прибора. Соответствующую величину принято называть приборной погрешностью. В общем случае она может иметь две составляющие – систематическую и случайную. У пра-вильно настроенного и поверенного измерительного прибора систематическая погрешность либо отсутствует, либо просто учитывается. Для определения приборной погрешности, связанной со случайными факторами, мы будем пользоваться следующими правилами. 1. Если прибор имеет класс точности (его величина указывается в паспорте и (или) на шкале прибора), то приборная погрешность определяется формулой
d = k П/100, (В.6)
где k – величина класса точности прибора; П – предел измерения прибора. 2. Если прибор не имеет класса точности, то приборная погрешность определяется половиной цены деления шкалы прибора. Так, определяемая приборная погрешность показывает максимально возможное отклонение показаний прибора от «истинного» значения измеряемой величины, обусловленное случайными факторами, связанными с процедурой измерения с помощью данного прибора. Ей соответствует значение доверительной вероятности P =100 %. Если в процессе многократных измерений выясняется, что основной вклад в случайную погрешность вносит приборная погрешность, то в данном эксперименте можно ограничиться однократными измерениями. На практике мы чаще всего имеем дело именно с ними. В этом случае оценка «истинного» значения измеряемойвеличины будет определяться однократным показанием прибора, а оценка погрешности измерения – приборной погрешностью. Если же основной вклад определяется не приборной погрешностью, то принципиальным становится именно проведение многократных измерений. В таком случае необходимо проводить статистическую обработку результатов многократных измерений (см. п. В.2). В качестве оценки «истинного» значения при этом будет выступать величинасреднего значения, а в качестве оценки погрешности – доверительная погрешность.
Цель работы
В пункте формулируется цель конкретной лабораторной работы.
Таблица измерительных приборов
В таблице приводятся основные сведения об используемыхизмерительных приборах.
Исходные данные и рабочие формулы
В пункте приводятся данные из паспорта экспериментальной установки, константы, необходимые для вычислений, и формулы, по которым будут вычисляться величины и их погрешности в данной лабораторной работе.
Таблица измерений В пункте приводится таблица, в которую заносятся результаты прямых и косвенных измерений.
6. Расчет
В пункте приводится по одному примеру расчета каждой величины и ее погрешности. Для этого показывается подстановка конкретных значений в рабочую формулу и записывается полученный при этом результат вычислений. Результаты Приводятся окончательные результаты измерений: полученное среднее значение с погрешностью, таблица результатов или график.
Вывод В пункте приводится вывод, полученный в процессе анализа результатов эксперимента. Вывод должен касаться сравнения теоретических предсказаний с экспериментальными данными, характерных значений полученных величин и их погрешностей, возможных факторов, определяющих систематические погрешности измерений.
Литература Приводится список литературы, использованной в процессе подготовки и при выполнении лабораторной работы.
В.7. Приложение к протоколу Как было сказано выше, протокол является формой представления результатов лабораторных измерений с их последующей математической обработкой. Для ряда лабораторных работ требуется до выполнения измерений получить ожидаемые теоретические результаты. Это позволяет студентам, во-первых, лучше разобраться с тем кругом физических понятий и законов, которые будут изучаться в лабораторной работе, и, следовательно, осознанно проводить опыты, и, во-вторых, сравнив ожидаемые теоретические результаты с результатами, полученными в ходе эксперимента, сделать обоснованное заключение о применимости использованной теории. Задание по теоретическому расчету студенты выполняют в процессе подготовки к лабораторной работе. Явившись на занятие, студент обязан показать преподавателю полученные теоретические результаты вместе с заготовкой протокола. Это – необходимое условие допуска к выполнению экспериментов. Одновременно с протоколом, содержащим результаты опытов, студент сдает теоретические результаты, оформленные как приложение к протоколу. Обычно студенческая бригада, выполняющая лабораторную работу на одной установке, состоит из 2-3 человек. Рекомендуется каждому члену бригады присвоить один из номеров 1, 2, 3, распределив фамилии студентов по алфавиту. Каждый член бригады получает индивидуальное теоретическое задание в соответствии со своим номером, содержание которого приведено в описании лабораторной работы.
Лабораторная работа № 0
Определение объема тела Цилиндрической формы
Цель работы – на достаточно простом примере научиться проводить измерения физической величины, обрабатывать и представлять результаты прямых и косвенных измерений. Объем цилиндра рассчитывается по формуле
V = π d 2 h /4, (*)
где d – диаметр основания и h – высота цилиндра. Следовательно, объем тела цилиндрической формы можно определить из косвенного измерения, произведя прямые измерения диаметра и высоты.
Обработка и представление результатов прямых измерений
Так как у реального цилиндрического тела значения d и h, измеренных в разных местах и направлениях, могут оказаться разными, то следует произвести многократные измерения диаметра и высоты для нескольких сечений цилиндра. Если результаты многократных измерений получатся разными, то следует произвести их статистическую обработку в соответствии с п. В.2. Предстоит определить средние значения d и h, среднеквадратичные отклонения Sd и Sh, доверительные погрешности D d и D h (доверительную вероятность следует выбирать близкую к 100 %). В качестве измерительного прибора в данной работе Вы будете использовать линейку или штангенциркуль. Прибор позволит Вам измерить диаметр и высоту цилиндра. Приборная погрешность δ линейки и штангенциркуля определяется ценой деления. Приступая к измерениям, Вам необходимо определить цену деления измерительного прибора. Доверительные погрешности D d и D h, полученные в результате статистической обработки, следует сравнить с приборной погрешностью δ. Если, например, большим оказывается значение d d, то результат многократных прямых измерений диаметра представляется в виде
d ± D d (n =..., P =...).
Если выполняется условие δ > D d, то результат представляется в виде d ± δ.
В последнем случае считается, что все имеющиеся случайные погрешности перекрываются погрешностью прибора. Именно в такой ситуации можно ограничиваться однократным измерением.
Обработка и представление результатов косвенного измерения
Возможны два варианта обработки и представления результатов косвенного измерения объема. I. По результатам многократных измерений d и h производятся многократные вычисления значений объема V. После этого производятся статистическая обработка и представление результатов в соответствии с п. В.2 в форме
V ± ∆ V (n =..., P =...).
II. Производится оценка среднего значения V путем подстановки средних значений d и h в формулу для вычисления объема. Оценка погрешности DV производится в соответствии с формулой (В.7), учитывающей связь погрешностей прямых и косвенных измерений. Результат представляется в форме V ± D V.
Строго говоря, варианты в общем случае дают разные результаты как для средних значений, так и для погрешностей величин, определяемых с помощью косвенных измерений. Но если погрешности существенно меньше самих величин, то результаты оказываются достаточно близкими. На практике чаще используется второй вариант, позволяющий сэкономить время на многократных вычислениях. А в том случае, когда прямые измерения являются однократными, это единственно возможный подход. Поэтому именно второй вариант представления результатов косвенных измерений Вам предстоит использовать в этой и в последующих лабораторных работах.
Задание к работе
1. Используя формулы (В.7) и (*), получите формулу для определения погрешности D V. Учтите, что при вычислении объема по формуле (*) число π округляется и, следовательно, характеризуется некоторой погрешностью округления. 2. Определите цену деления и приборную погрешность измерительного прибора. 3. Подготовьте протокол: – оформите титульный лист; – укажите цель работы в п. 1 протокола; – начертите и заполните таблицу измерительных приборов в п. 2; – запишите рабочие формулы в п. 3 (формула для определения средних значений величин, формула для определения среднеквадратичного отклонения, формула для определения доверительной погрешности, формула для определения объема, выведенная Вами формула для определения D V – погрешности косвенного измерения объема); – п. 4 отсутствует; – в п. 5 начертите две таблицы (см. табл. В.2) для обработки результатов многократных (n = 5) измерений диаметра и высоты цилиндра. 4. Произведите пятикратные измерения диаметра и высоты цилиндра в разных сечениях тела. Результаты измерений занесите в таблицы. 5. Произведите статистическую обработку результатов измерений. Определите средние значения диаметра и высоты, а также соответствующие им доверительные погрешности. Сравните доверительные погрешности с приборной погрешностью измерительного прибора. 6. Приведите оценку среднего значение объема цилиндра и соответствующей ему погрешности. 7. В п. 6 протокола продемонстрируйте, как проводились расчеты средних величин и их погрешностей. 8. В п. 7 протокола приведите окончательные результаты прямых и косвенных измерений в стандартной форме. 9. Проанализируйте полученные результаты, сделайте вывод и запишите его в п. 8 протокола.
Список литературы 1. Агекян Т.А. Основы теории ошибок для астрономов и физиков. – М: Наука, 1972. 2. Кассандрова О.Н., Лебедев В.В. Обработка результатов измерений. – М: Наука, 1970. 3. Сквайрс Дж. Практическая физика / Пер. с англ. – М.: Мир, 4. Тейлор Дж. Введение в теорию ошибок / Пер. с англ. – М.: Мир, 1985. 5. Худсон Д. Статистика для физиков / Пер. с англ. – М.: Мир, 1967.
Лабораторная работа № 1
Измерение скорости пули с помощью баллистического маятника
Цель работы – с помощью баллистического маятника определить скорость пуль с различными массами. Рабочую формулу для экспериментального определения скорости пули и теоретическую зависимость скорости пули от ее массы получить исходя из законов сохранения импульса и энергии.
Описание установки
Баллистический маятник представляет собой массивный цилиндр М, заполненный пластилином. В цилиндр в горизонтальном направлении производят выстрел пулей массы
Рис. 1.1
Задание к работе
1. Сделайте заготовку протокола к лабораторной работе. 2. Получите допуск к выполнению лабораторной работы у преподавателя. 3. Соблюдая правила техники безопасности, зарядите пружинный пистолет пулей с наибольшей массой. 4. Подготовьте устройство 5. Осуществите первый выстрел пулей с наибольшей массой, нажав спусковую кнопку пистолета. Запишите численное значение конечной координаты
Запишите величину 6. Проведите опыт с той же пулей пять раз, чтобы в дальнейшем провести статистическую обработку этих прямых измерений. 7. Проведите однократные измерения смещения маятника для пуль с другой массой (п. 3–5). 8. Проведите статистическую обработку прямых многократных измерений смещения маятника для первой пули согласно методике, описанной в [1]. Результаты внесите в таблицу измерений. 9. По формуле (1.9) получите оценку истинного значения скорости пули 10. Получите оценку абсолютной погрешности косвенных изме
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.018 с.) |


 , (В.2)
, (В.2) .
.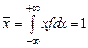
 . Поэтому величина x 0 и получила название среднего значения генерального (нормального) распределения, или генерального среднего.
. Поэтому величина x 0 и получила название среднего значения генерального (нормального) распределения, или генерального среднего.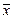 )2 f dx . Поэтому sназывается среднеквадратичным (стандартным) отклонением генерального (нормального) распределения, или генеральным отклонением. Среднеквадратичноеотклонение характеризует среднюю меру разброса (отклонения) случайной величины x от среднего значения
)2 f dx . Поэтому sназывается среднеквадратичным (стандартным) отклонением генерального (нормального) распределения, или генеральным отклонением. Среднеквадратичноеотклонение характеризует среднюю меру разброса (отклонения) случайной величины x от среднего значения  . (В.3)
. (В.3)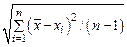 . (В.4)
. (В.4) из пружинного пистолета Р, неподвижно закрепленного вблизи маятника (рис. 1.1). Пуля проникает в пластилин, застревает в нем и дальше продолжает двигаться вместе с маятником (абсолютно неупругий удар). Маятник закреплен так, чтобы в процессе отклонения он совершал поступательное движение. Максимальное отклонение маятника от его положения равновесия фиксируется механизмом N.
из пружинного пистолета Р, неподвижно закрепленного вблизи маятника (рис. 1.1). Пуля проникает в пластилин, застревает в нем и дальше продолжает двигаться вместе с маятником (абсолютно неупругий удар). Маятник закреплен так, чтобы в процессе отклонения он совершал поступательное движение. Максимальное отклонение маятника от его положения равновесия фиксируется механизмом N.
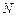 к измерению горизонтального смещения маятника. Запишите численное значение начальной координаты
к измерению горизонтального смещения маятника. Запишите численное значение начальной координаты 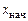 маятника по линейке отсчетного устройства
маятника по линейке отсчетного устройства 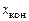 , определив его по линейке отсчетного устройства
, определив его по линейке отсчетного устройства 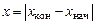 .
. в таблицу измерений.
в таблицу измерений.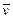 , для которой были проведены многократные измерения. Результат внесите в таблицу измерений. Рекомендуется для получения скорости пули использовать результаты индивидуального задания для членов бригады, выполняющих лабораторную работу на одной установке.
, для которой были проведены многократные измерения. Результат внесите в таблицу измерений. Рекомендуется для получения скорости пули использовать результаты индивидуального задания для членов бригады, выполняющих лабораторную работу на одной установке.


